Analysis of non-Darcy forced convection heat transfer in a porous circular duct under LTNE condition
-
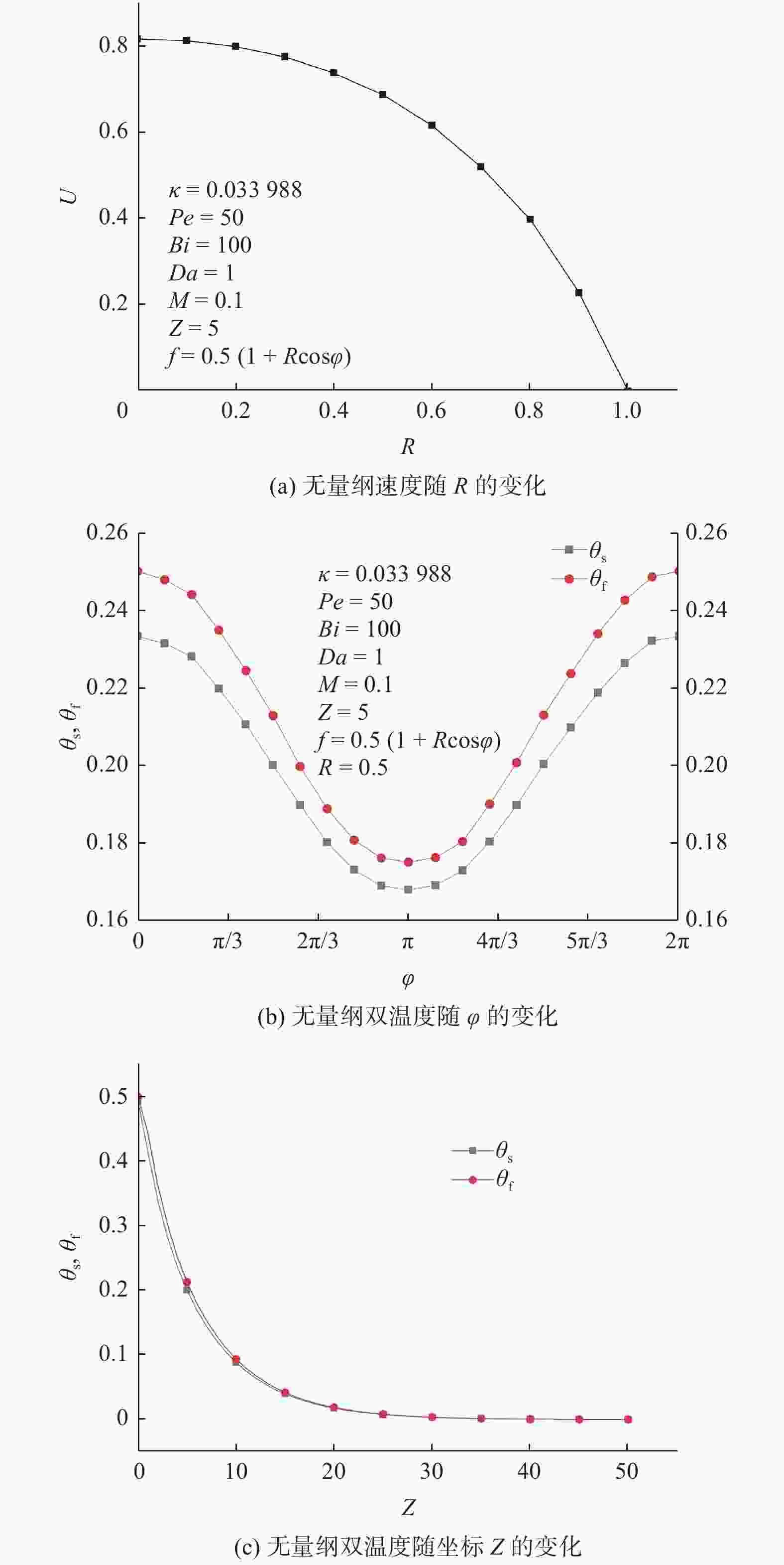
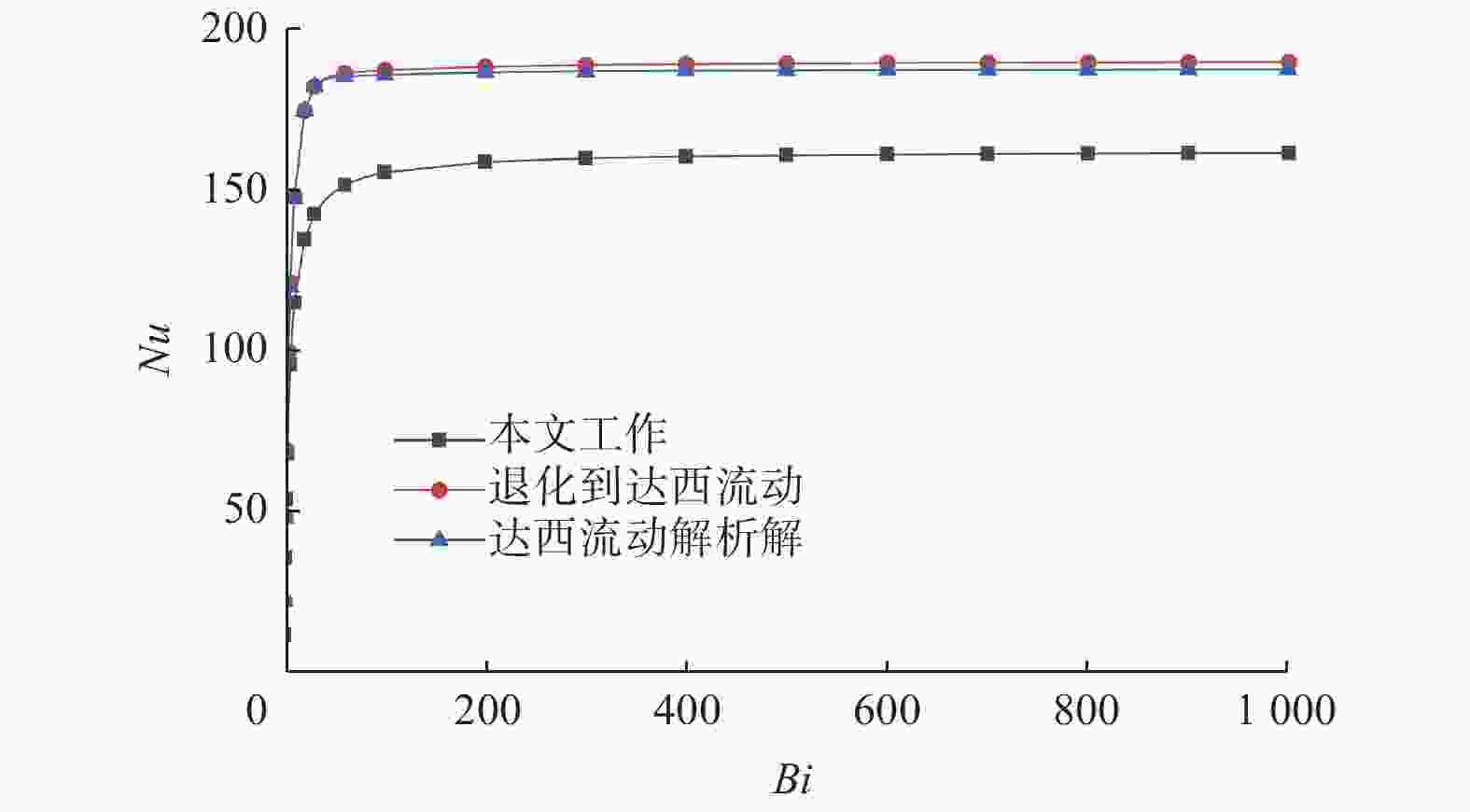
摘要: 对流体饱和多孔介质圆管内局部热非平衡情形下非达西强迫对流的换热性能进行数值模拟. 首先利用Brinkman流动模型和局部热非平衡模型建立研究问题的数学模型，预测强迫对流换热. 然后使用COMSOL Multiphysics仿真软件对模型求解，获得无量纲渗流速度场、固体骨架温度场、流体温度场和努塞尔数(
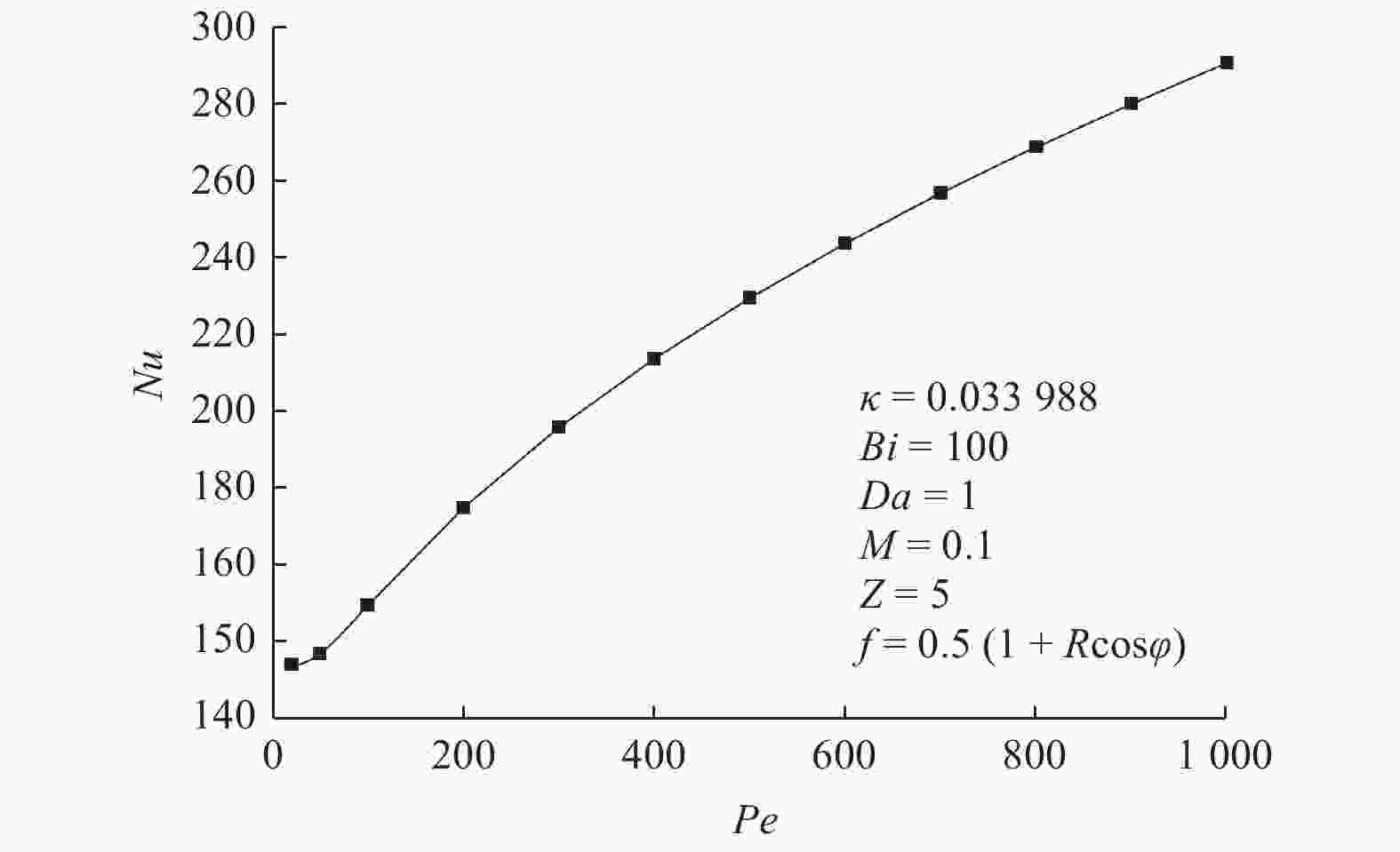
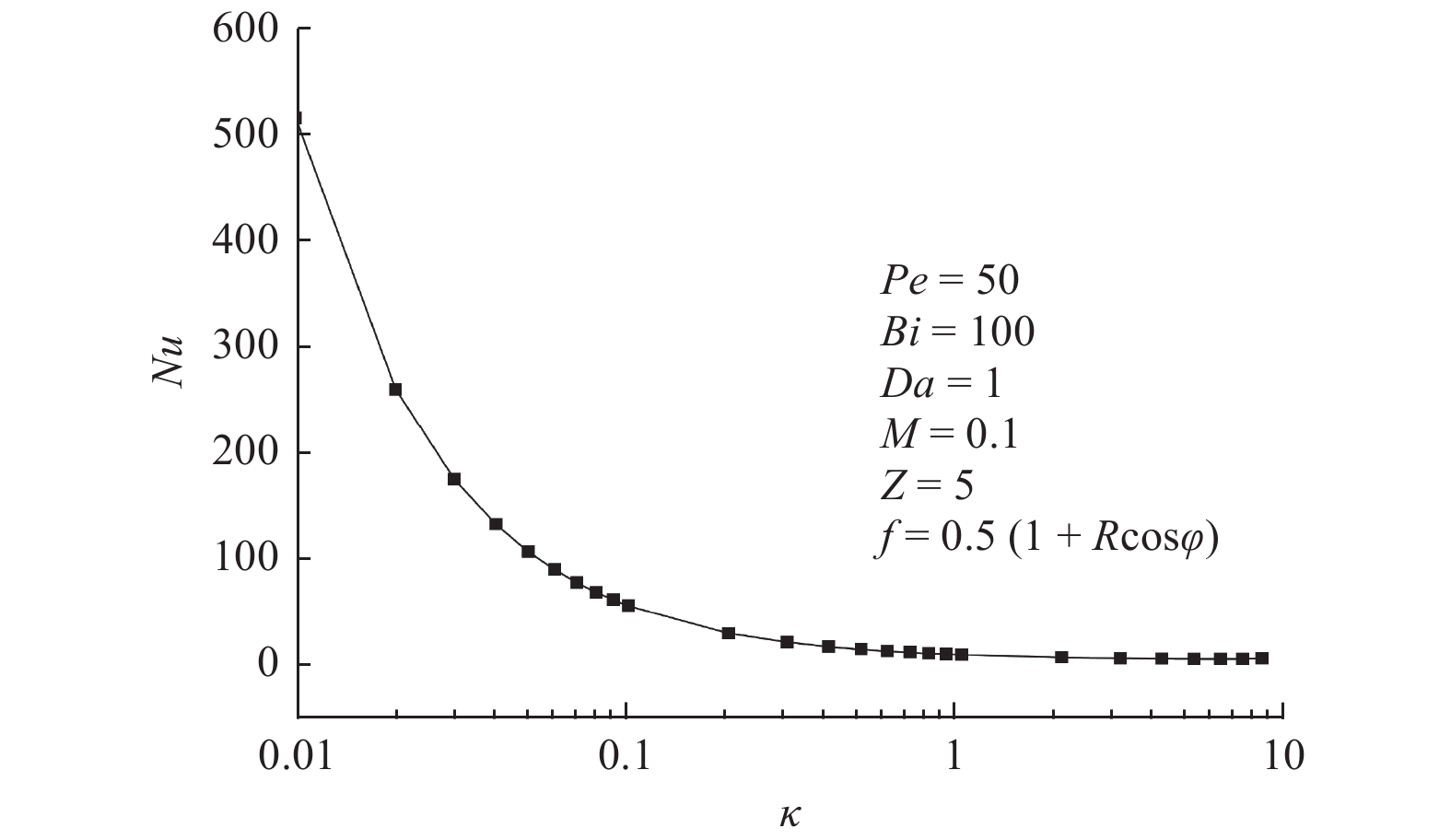
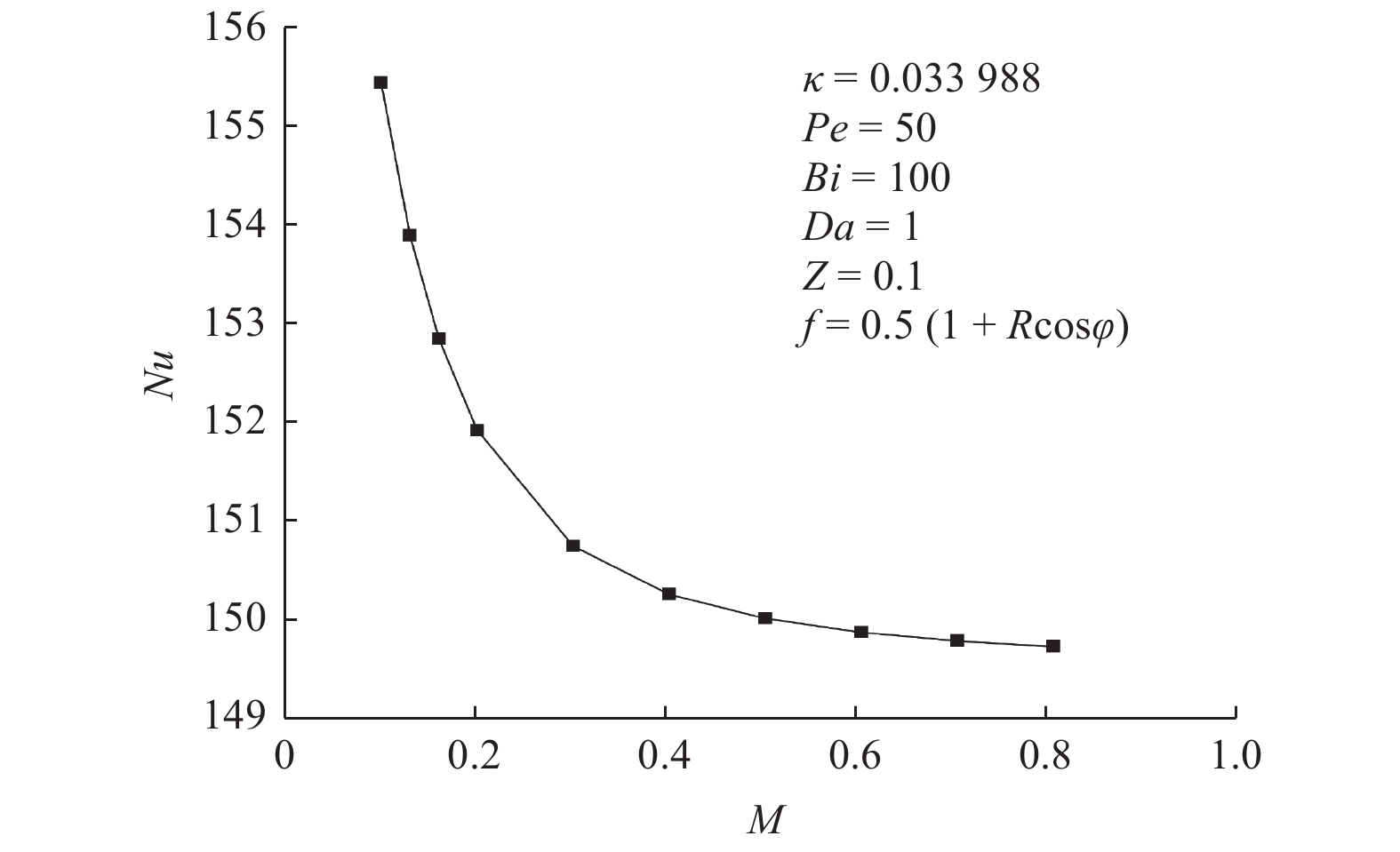
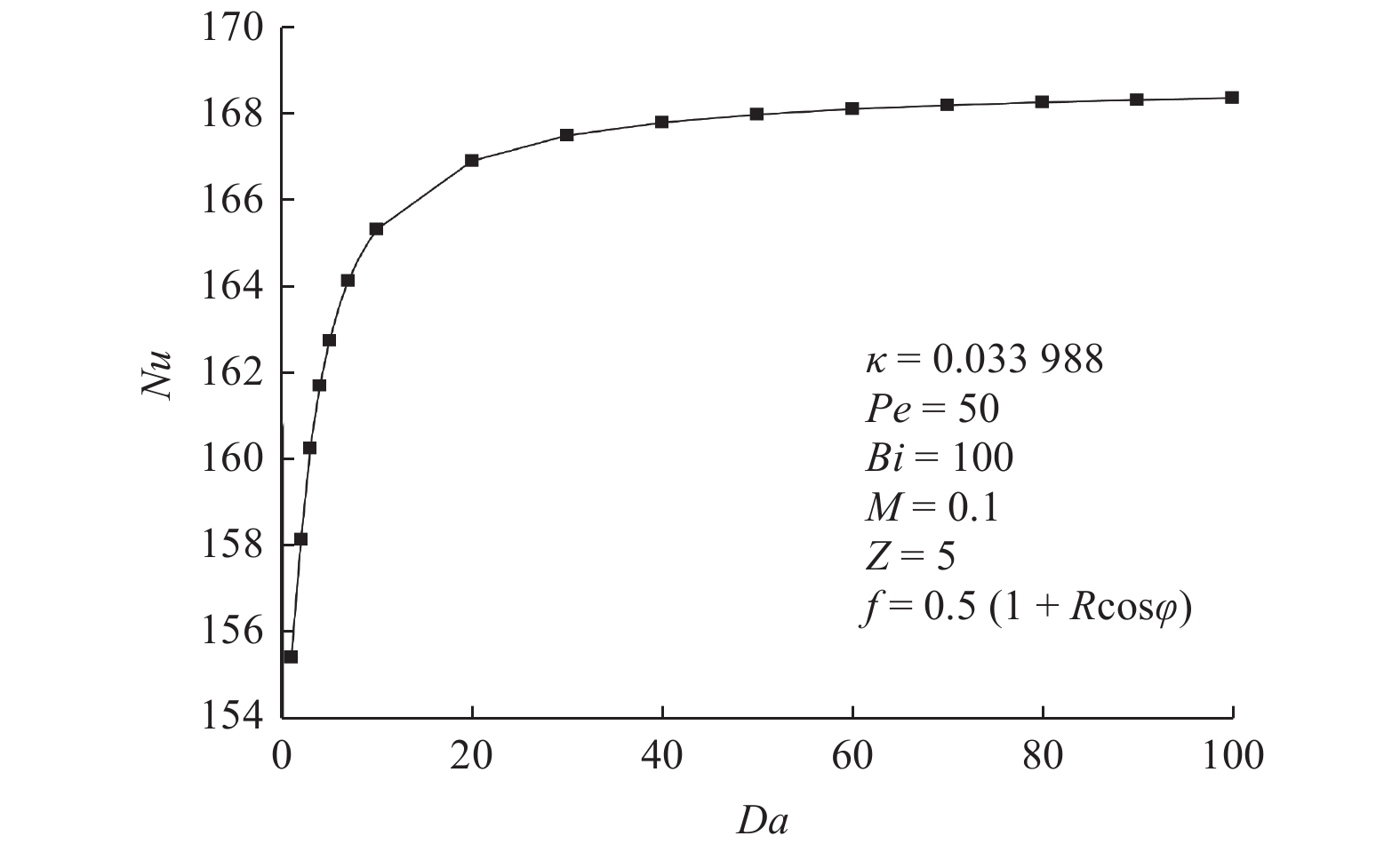
$Nu$ ). 此外，详细分析$Nu$ 对某些关键参数的依赖性. 研究发现，随着达西数($Da$ )和毕渥数($Bi$ )的增加，$Nu$ 先增加后趋于渐近值；贝克来数($Pe$ )的增加会导致$Nu$ 单调增加；相反，流体有效热导率与固体骨架有效热导率之比(即导热比$\kappa $ )和流体有效动力黏度与实际动力黏度比(即黏度比M)的增加将导致$Nu$ 先减小后趋于渐近值. 所得模型和数值结果既可用于提高工程中多孔介质圆管换热能力，也可为相关实验和解析研究提供参考.Abstract: The heat transfer performance of non-Darcy forced convection in a fluid-saturated porous tube under local thermal non-equilibrium was numerically simulated. Firstly, the Brinkman flow model and the local thermal non-equilibrium (LTNE) model were employed to establish the mathematical model of the studied problem to predict the forced convective heat transfer. Then, the mathematical model was numerically solved using COMSOL Multiphysics simulation software. And the fluid velocity field, the solid temperature field, the fluid temperature field, and the Nusselt number were obtained. Moreover, the dependences of the Nusselt number ($Nu$ ) on some key parameters were analyzed in detail. It was found that the Nusselt number increases first and then tends to approach an asymptotic value with the increase of the Darcy number ($Da$ ) and the Biot number ($Bi$ ). The Nusselt number monotonously increases with increasing the Péclet number ($Pe$ ). On the contrary, the Nusselt number decreases first and then tends to be an asymptotic value owing to the increase of the ratio of effective thermal conductivity of fluid to effective thermal conductivity of solid (the thermal conductivity ratio$\kappa $ ) and ratio of effective dynamic viscosity of fluid to actual dynamic viscosity (the viscosity ratio M). The model and numerical results obtained can not only be used to improve the heat transfer capacity of porous medium pipes in engineering, but also provide references for related experiments and analytical studies. -
图 2 无量纲速度和温度随坐标的变化
Figure 2. Variation of dimensionless velocity and temperature with coordinates
图 5
${\boldsymbol{Nu}}$ 随${\boldsymbol{Bi}}$ 的变化Figure 5. Variations of Nu with
${\boldsymbol{Bi}}$ 
图 6
${\boldsymbol{Nu}}$ 随${\boldsymbol{Pe}}$ 的变化Figure 6. Variations Nu of with
${\boldsymbol{Pe}}$ 
图 7
${\boldsymbol{Nu}}$ 随${\boldsymbol{\kappa}}$ 的变化Figure 7. Variations Nu of with
${\boldsymbol{\kappa }}$ 表 1 符号表
Table 1. Symbol table
符号 含义 符号 含义 ${T_{\rm{s}}}$ 固体温度/ ℃ $u$ 流体速度/ $ {\rm{(m}}\cdot {\rm{s}}^{\rm{-1}}\rm{)}$ ${T_{\rm{f}}}$ 流体温度/ ℃ $\rho $ 密度/ $ {\rm{(kg }}\cdot{\rm{m}}^{\rm{-3}}\rm{)}$ ${\mu _{{\rm{eff}}}}$ 流体有效动力黏度/ $({\rm{kg}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}\cdot{{\rm{s}}^{{\rm{ - 1}}}})$ ${c_p}$ 比热容/ $ ({\rm{J}}\cdot{\rm{k}}{{\rm{g}}^{{\rm{ - 1}}}}\cdot{{\rm{K}}^{{\rm{ - 1}}}})$ $\mu $ 流体实际动力黏度/ $({\rm{kg}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}\cdot{{\rm{s}}^{{\rm{ - 1}}}})$ $K$ 渗透率/ ${\rm{m} }^{2}$ $h$ 固液界面传热系数/ $({\rm{W} }\cdot{ {\rm{m} }^{ {\rm{ - 2} } } }\cdot{ {\rm{K} }^{ {\rm{ - 1} } } })$ ${k_{{\rm{s,eff}}}}$ 固体有效热导率/ $ ({\rm{W}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}\cdot{{\rm{K}}^{{\rm{ - 1}}}})$ ${k_{{\rm{f,eff}}}}$ 流体有效热导率/ $ ({\rm{W}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}\cdot{{\rm{K}}^{{\rm{ - 1}}}})$ $\phi $ 孔隙率 ${k_{\rm{s}}}$ 固体热导率/ $ ({\rm{W}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}\cdot{{\rm{K}}^{{\rm{ - 1}}}})$ ${k_{\rm{f}}}$ 流体热导率/ $ ({\rm{W}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}\cdot{{\rm{K}}^{{\rm{ - 1}}}})$ 
下载: 导出CSV
-
[1] NIELD D A, KUZNETSOV A V, XIONG M. Thermally developing forced convection in a porous medium: Parallel plate channel with walls at uniform temperature, with axial conduction and viscous dissipation effects[J] . International Journal of Heat and Mass Transfer,2003,46(4):643 − 651. doi: 10.1016/S0017-9310(02)00327-7 [2] QU Z G, XU H J, TAO W Q. Fully developed forced convective heat transfer in an annulus partially filled with metallic foams: An analytical solution[J] . International Journal of Heat and Mass Transfer,2012,55(25):7508 − 7519. [3] WANG K Y, VAFAI K, LI P C, et al. Forced convection in a bidisperse porous medium embedded in a circular pipe[J] . Journal of Heat Transfer,2017,139(10):102601. doi: 10.1115/1.4036574 [4] NIELD D A, BEJAN A. Mechanics of fluid flow through a porous medium in convection in porous media[J] . Convection in Porous Media,2017:1 − 35. [5] 钟家伦, 李培超. 非均匀温度边界下多孔介质太阳能吸热管内非达西强迫对流传热数值研究[J] . 轻工机械,2018,36(4):30 − 34;39. doi: 10.3969/j.issn.1005-2895.2018.04.006 [6] LI P C, ZHONG J L, WANG K Y, et al. Analysis of thermally developing forced convection heat transfer in a porous medium under local thermal non-equilibrium condition: A circular tube with asymmetric entrance temperature[J] . International Journal of Heat and Mass Transfer,2018,127:880 − 889. doi: 10.1016/j.ijheatmasstransfer.2018.08.081 [7] YANG K, VAFAI K. Restrictions on the validity of the thermal conditions at the porous-fluid interface: An exact solution[J] . Journal of Heat Transfer,2011,133(11):112601. doi: 10.1115/1.4004350 [8] BRINKMAN H C. A calculation of the viscous force exerted by a flowing fluid in a dense swarm of particles[J] . Applied Scientific Research,1949,1(1):27 − 34. [9] VAFAI K, TIEN C L. Boundary and inertia effects on convective mass transfer in porous media[J] . International Journal of Heat and Mass Transfer,1982,25(8):1183 − 1190. doi: 10.1016/0017-9310(82)90212-5 [10] NITHIARASU P, SEETHARAMU K N, SUNDARARAJAN T. Natural convective heat transfer in a fluid saturated variable porosity medium[J] . International Journal of Heat and Mass Transfer,1997,40(16):3955 − 3967. doi: 10.1016/S0017-9310(97)00008-2 [11] NIELD D A, KUZNETSOV A V, XIONG M. Effect of local thermal non-equilibrium on thermally developing forced convection in a porous medium[J] . International Journal of Heat and Mass Transfer,2002,45(25):4949 − 4955. doi: 10.1016/S0017-9310(02)00203-X [12] KUZNETSOV A V, NIELD D A. Forced convection with laminar pulsating flow in a saturated porous channel or tube[J] . Transport in Porous Media,2006,65(3):505 − 523. doi: 10.1007/s11242-006-6791-6 [13] CEKMER O, MOBEDI M, OZERDEM B. Fully developed forced convection heat transfer in a porous channel with asymmetric heat flux boundary conditions[J] . Transport in Porous Media,2011,90(3):791 − 806. doi: 10.1007/s11242-011-9816-8 [14] SEETHARAMU K N, LEELA V, KOTLONI N. Numerical investigation of heat transfer in a micro-porous-channel under variable wall heat flux and variable wall temperature boundary conditions using local thermal non-equilibrium model with internal heat generation[J] . International Journal of Heat & Mass Transfer,2017,112:201 − 215. doi: 10.1016/j.ijheatmasstransfer.2017.04.068 [15] BUONOMO B, CASCETTA F, LAURIAT G, et al. Convective heat transfer in thermally developing flow in micro-channels filled with porous media under local thermal non-equilibrium conditions[J] . Energy Procedia,2018,148:1058 − 1065. doi: 10.1016/j.egypro.2018.08.054 [16] XU H J, QU Z G, TAO W Q. Analytical solution of forced convective heat transfer in tubes partially filled with metallic foam using the two-equation model[J] . International Journal of Heat and Mass Transfer,2011,54(17):3846 − 3855. [17] WANG K Y, TAVAKKOLI F, VAFAI K. Analysis of gaseous slip flow in a porous micro-annulus under local thermal non-equilibrium condition: An exact solution[J] . International Journal of Heat & Mass Transfer,2015,89:1331 − 1341. doi: 10.1016/j.ijheatmasstransfer.2015.06.001 [18] XU Z G, GONG Q. Numerical investigation on forced convection of tubes partially filled with composite metal foams under local thermal non-equilibrium condition[J] . International Journal of Thermal Sciences,2018,133:1 − 12. doi: 10.1016/j.ijthermalsci.2018.06.014 [19] LI P C, ZHANG J L, WANG K Y, et al. Heat transfer characteristics of thermally developing forced convection in a porous circular tube with asymmetric entrance temperature under LTNE condition[J] . Applied Thermal Engineering,2019,154:326 − 331. doi: 10.1016/j.applthermaleng.2019.03.109 [20] PANGRLE B J, ALEXANDROU A N, DIXON A G, et al. An analysis of laminar fluid flow in porous tube and shell systems[J] . Chemical Engineering Science,1991,46(11):2847 − 2855. doi: 10.1016/0009-2509(91)85153-O -
下载:
点击查看大图
图(9) / 表(1)
计量
- 文章访问数: 459
- HTML全文浏览量: 746
- PDF下载量: 224
- 被引次数: 0
