Study on reliability of metro vehicle doors based on exponential distribution and RAMS
-
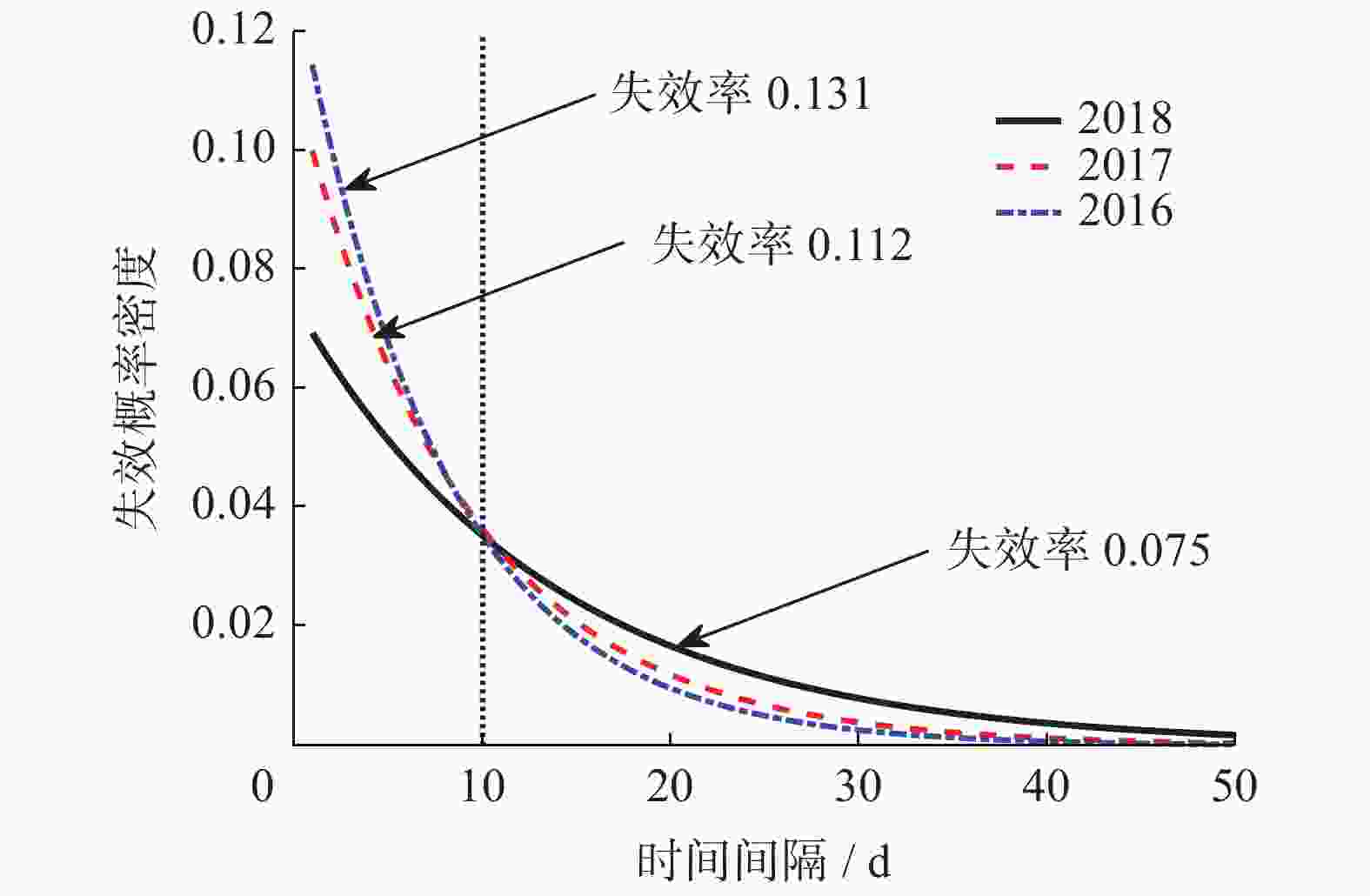
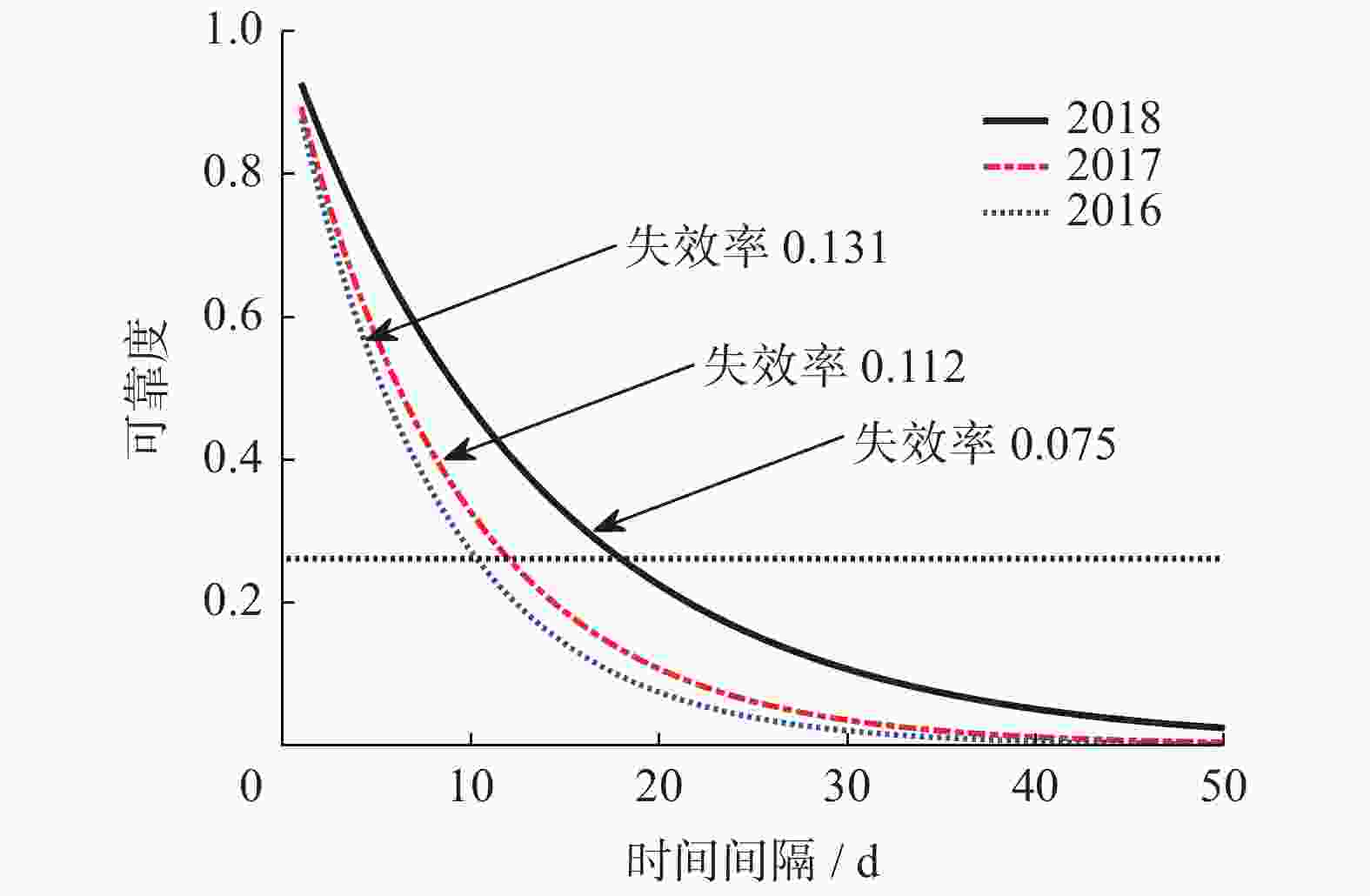
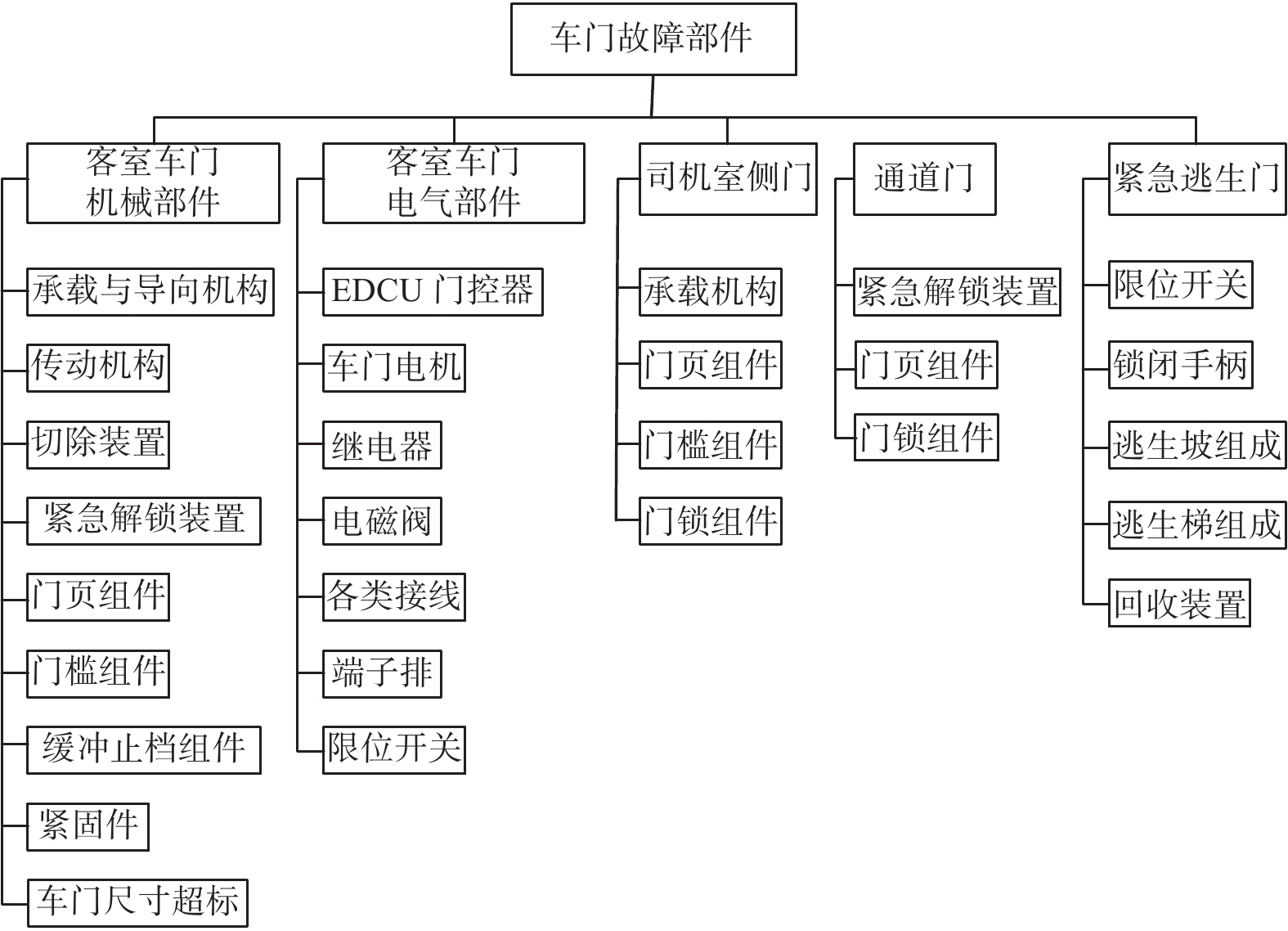
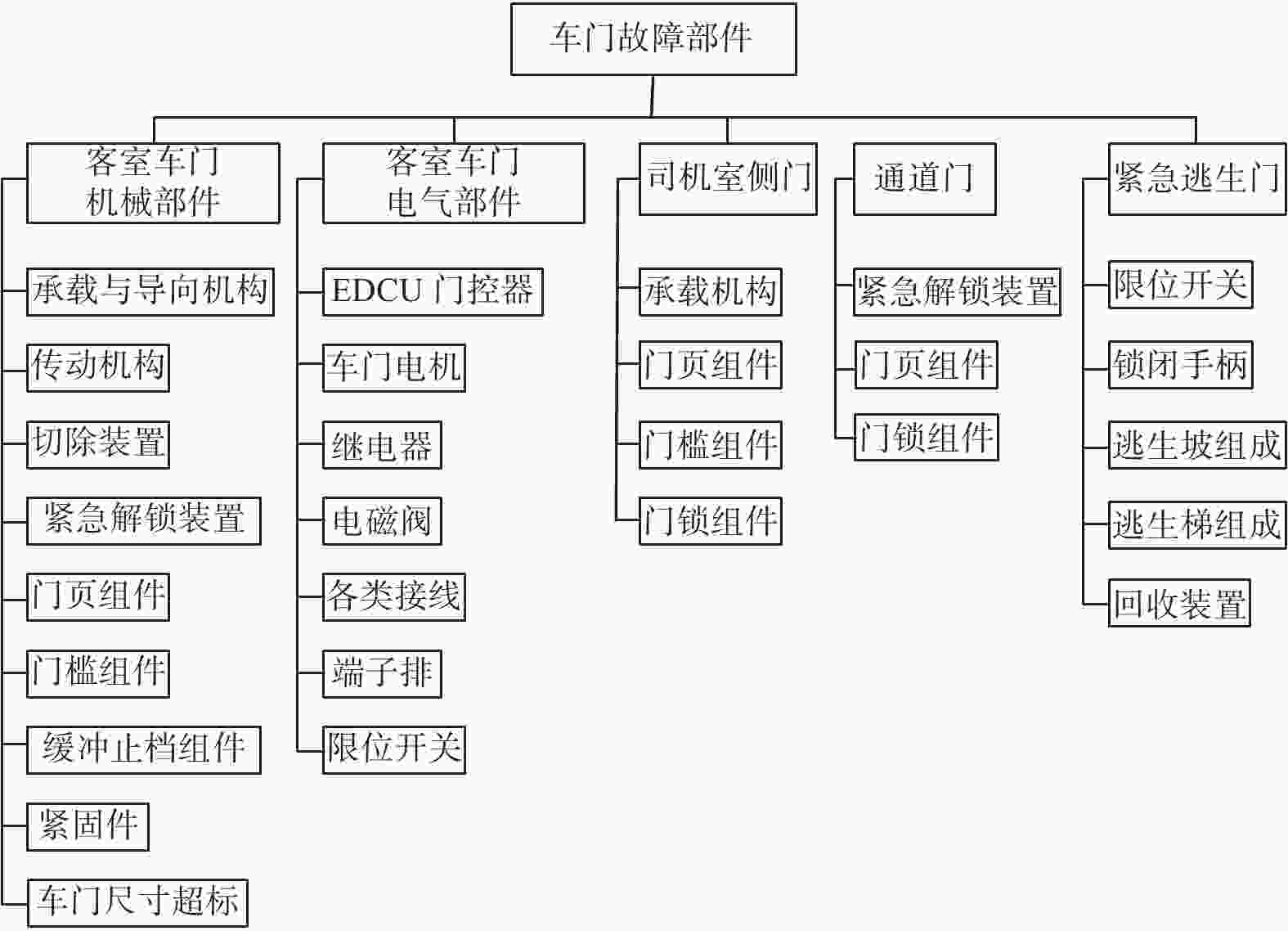
摘要: 以预防和减少地铁车门故障为目的，根据上海地铁13号线路3年车门故障统计数据，利用指数分布函数对3年车门故障时间间隔进行分析. 结合可靠性、可用性、维修性和安全性（RAMS）中的可靠性理论，分析3年车门的可靠性，以列车车门综合可靠度为目标，提出确定车门预防性检修周期的方法. 结果表明：3年车门故障时间间隔都服从指数分布函数；车门失效率决定车门的可靠性，车门失效率越小，车门可靠性越高，其车门工作时间越长，反之，车门工作时间越短；建议列车车门除了日常必需的检修维护，还可根据每年的车门故障数据获得动态预防性检修周期，做到特定年份特定设置预防性检修周期，从而提高列车车门的可靠性. 该方法为提高列车车门的可靠性提供了参考依据.Abstract: For the purpose of preventing and reducing metro door failures, an exponential distribution function was used to analyze the door failure time intervals based on statistical data of three-year door failures on Shanghai metro line 13. Combined with the reliability theory in RAMS, the reliability of doors in three years was analyzed, and a method to determine the preventive maintenance cycle of doors with the comprehensive reliability of train doors as the goal was put forward. The results show that the three-year door failure time interval obeys exponential distribution function and door failure rate determines the reliability of the door. The smaller the door failure rate, the higher the reliability of the door and the longer the working time of the door; otherwise the shorter the working time of the door. It was suggested that in addition to the daily necessary maintenance of train doors, dynamic preventive maintenance cycle can be obtained according to the annual door failure data, so that the preventive maintenance cycle can be set in a specific year, thus improving the reliability of train doors. The method can provide a reference for improving the reliability of the door.
-
Key words:
- door failure /
- exponential distribution /
- maintenance cycle /
- reliability
-
图 2 车门故障时间间隔指数分布拟合曲线图
Figure 2. Fitting curve diagram of door failure time interval exponential distribution
表 1 车门故障时间间隔假设性检验
Table 1. Hypothesis test of door failure time interval
年份 样本数量 指数参数 p值 均值 $\lambda $ 2016 47 7.68 0.131 0.212 2017 37 8.95 0.112 0.802 2018 20 13.40 0.075 0.746 
下载: 导出CSV
表 3 不同可靠度下的车门预防性检修周期
Table 3. Preventive maintenance cycle of door under different reliability
列车综合可靠度 0.90 0.95 0.99 失效率$\lambda $ 0.075 0.075 0.075 预防检修周期 87 42 8
下载: 导出CSV
-
[1] 张桥平, 彭建武, 周志刚. 城市轨道交通车辆机械[M]. 成都: 西南交通大学出版社, 2012. [2] 陈苏雨, 方宇, 胡定玉. 基于随机森林方法的地铁车门故障诊断[J] . 测控技术,2018,37(2):20 − 24. doi: 10.3969/j.issn.1000-8829.2018.02.006 [3] 詹文元. 深圳地铁1号线一期工程车辆车门控制器故障分析及改进[J] . 电力机车与城轨车辆,2014(4):88 − 89. [4] 丁心凡. 北京地铁4号线列车车门故障的改进分析[J] . 铁道机车车辆,2016(6):101 − 104. doi: 10.3969/j.issn.1008-7842.2016.06.26 [5] 赵伟龙. 广州地铁3号线RLS−E2型车门的维修及故障分析[J] . 机车电传动,2016(5):120 − 124. [6] 陈卓群, 林沛扬. 广州市轨道交通七号线列车车门紧急解锁故障分析及改造[J] . 电力机车与城轨车辆,2018,41(6):79 − 81. [7] 牟颖. 地铁列车车门故障诊断与可靠性分析[D]. 大连: 大连交通大学, 2018. [8] 陈超. 城市轨道车辆自动塞拉门系统研究[D]. 南京: 南京理工大学, 2003. [9] 任金宝, 邢宗义. 基于Minitab统计分析软件的地铁车辆车门可靠性评估方法研究[J] . 城市轨道交通研究,2015,18(9):90 − 94. [10] 曾华, 刘雁鸣, 熊德之. 概率论与数理统计[M]. 北京: 科学出版社, 2014. -
下载:
点击查看大图
图(5) / 表(3)
计量
- 文章访问数: 430
- HTML全文浏览量: 349
- PDF下载量: 139
- 被引次数: 0
