Dynamics characteristics of circular restricted three-body problem
-
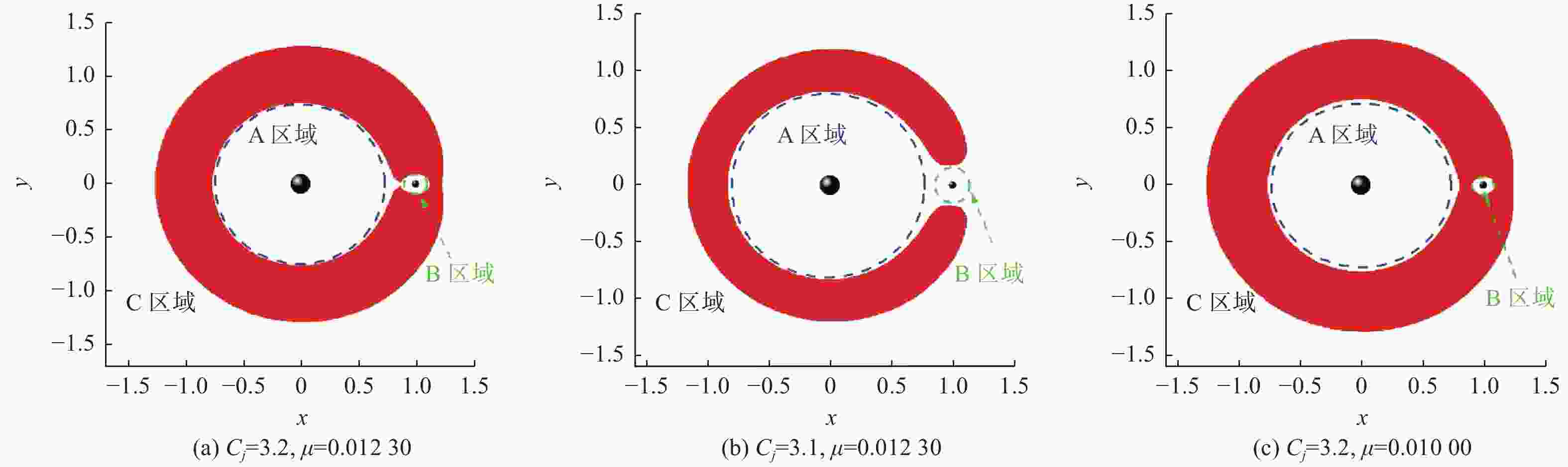
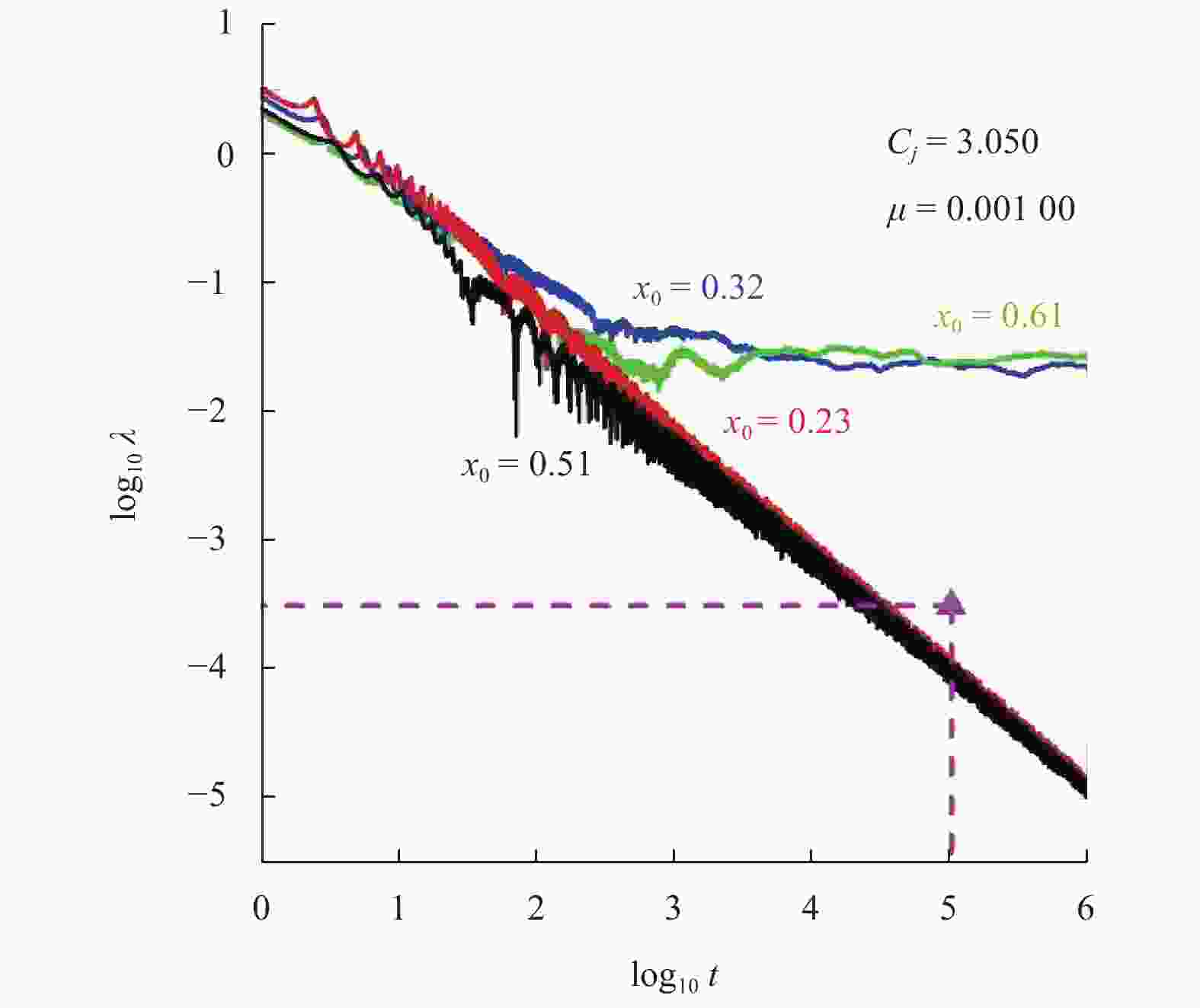
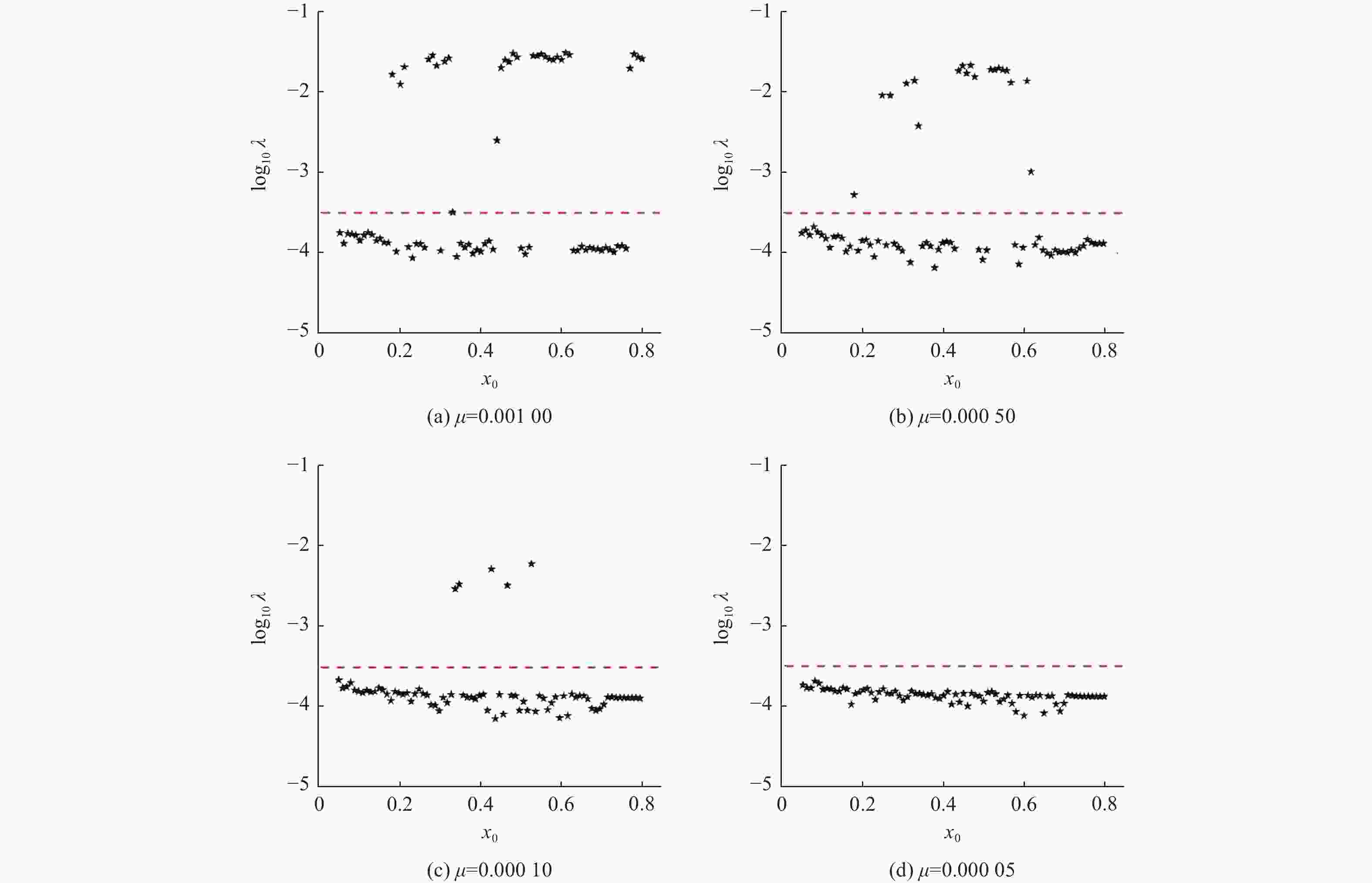
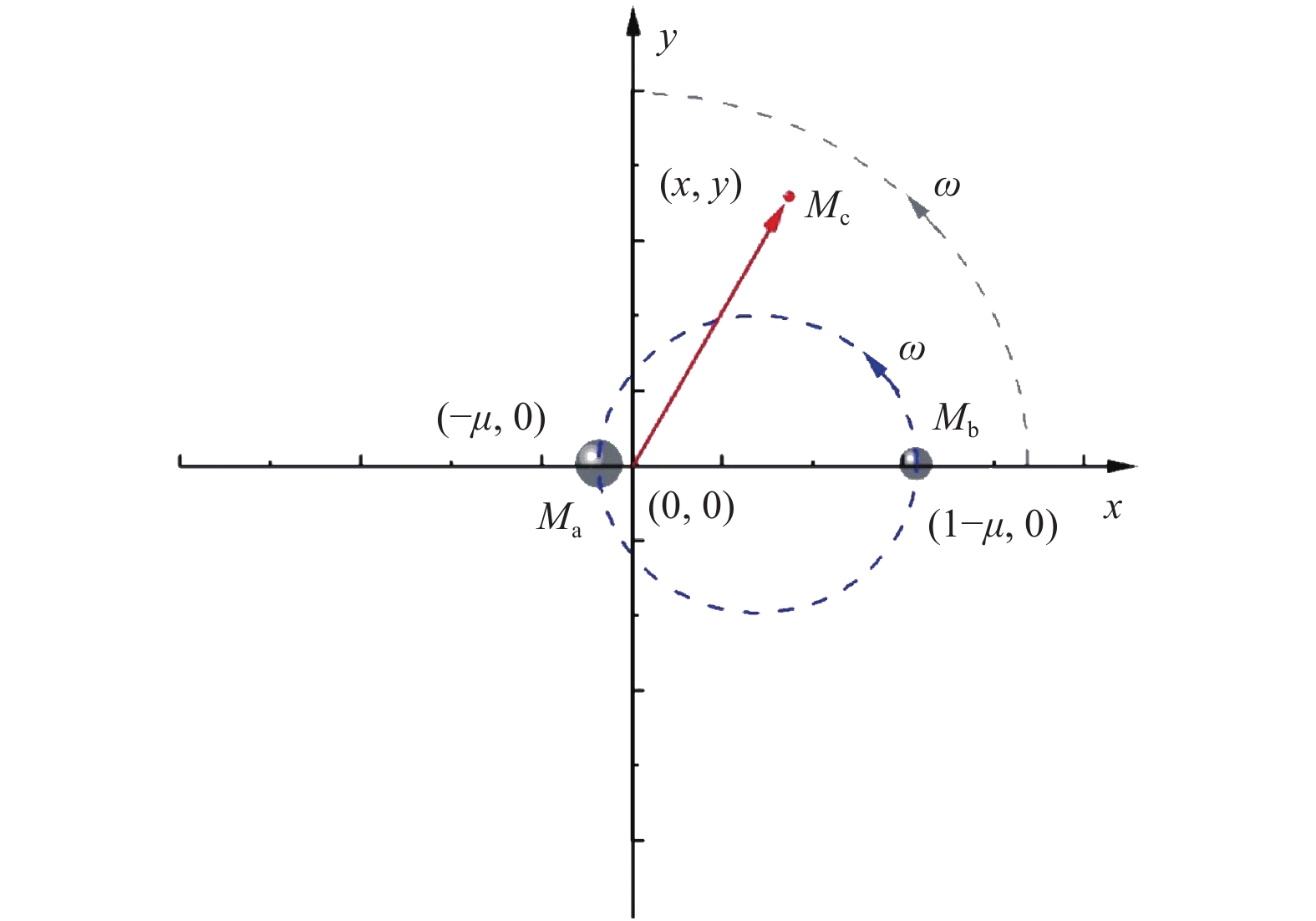
摘要: 禁行域在圆型限制性三体问题中对第三体的运动有极为重要的影响. 利用零速度曲线讨论天体禁行域与系统参数之间的关系. 禁行域与雅可比常数有关，且能影响天体的运动区域和轨道构型. 利用最大李雅普诺夫指数寻找该模型的混沌轨道，给出混沌轨道在不同系统参数下随天体初始位置的分布. 这些分布说明，当第三天体从两主天体连线的中点处释放时，容易产生混沌运动；当质量参量足够小时，体系无法产生混沌现象.Abstract: The forbidden zone has a significantly important influence on the motion of the third body in the circular restricted three-body problem. Based on zero-velocity curves, the relationship between the forbidden zone of celestial bodies and dynamical parameters was discussed. It was obtained that the forbidden zones are related to the Jacobian constant, and can affect motion areas of celestial bodies and dynamical types of orbits. The maximum Lyapunov exponents were used to find chaotic orbits, and the distributions of chaotic orbits with respect to the initial positions of the celestial bodies for different dynamical parameters were given. These distributions indicate that when the third celestial body is released from the midpoint of the two main celestial bodies, chaos easily occurs. However, there is no chaos when the mass parameter is small sufficiently.
-
Key words:
- restricted three-body problem /
- Hamiltonian system /
- numerical simulation /
- orbit /
- chaos
1) 八九阶变步长龙格−库塔法[RKF8(9)]是一种高精度、可自适应步长的数值积分算法. 此算法可以在不同的积分步数中，自动选择最优步长，尽可能减少舍入误差，并在一定积分时间内将系统守恒量（如本文的雅可比常数Cj）误差维持在机器精度.2) 系统不可积是存在混沌轨道的必要非充分条件. -
图 1 三体系统在旋转坐标系中的运动示意图
Figure 1. Sketch map of motion of three-body system in rotating frame
图 2 不同参数下第三天体的运动区域和禁行域示意图
Figure 2. Sketch maps of motion region and forbidden zone of the third body for different parameters
图 3 雅可比常数Cj = 3.003时不同轨道示意图
Figure 3. Sketch maps of different orbits when Jacobi constant Cj = 3.003
图 5 雅可比常数Cj = 3.050时不同轨道示意图
Figure 5. Sketch maps of different orbits when the Jacobi constant Cj = 3.050
图 4 雅可比常数Cj = 3.010时不同轨道示意图
Figure 4. Sketch maps of different orbits when Jacobi constant Cj = 3.010
图 7 不同质量参量下最大李雅普诺夫指数λ与初始坐标x0的关系
Figure 7. Relations between the maximum Lyapunov exponents λ and initial coordinates x0 for different mass parameters
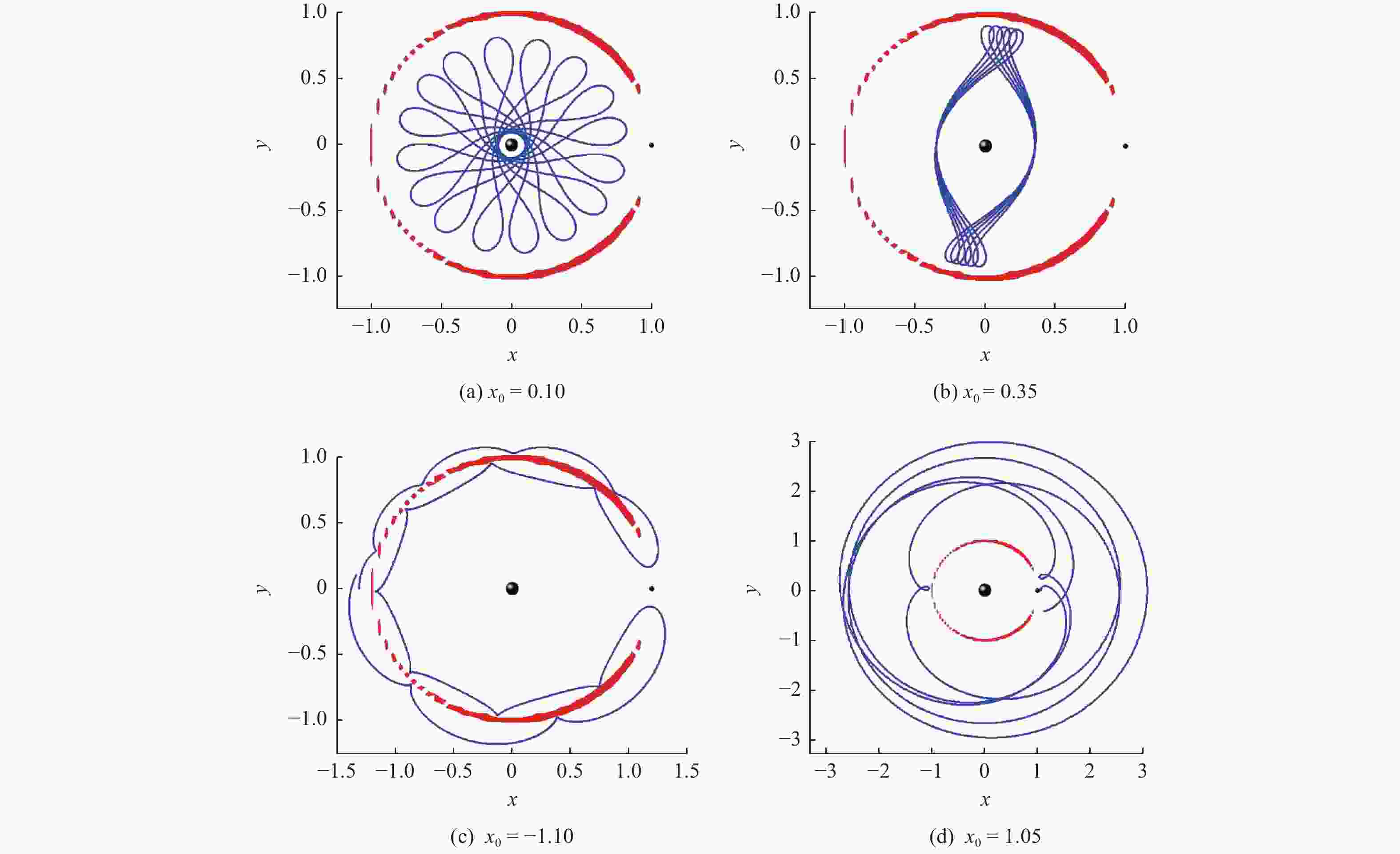
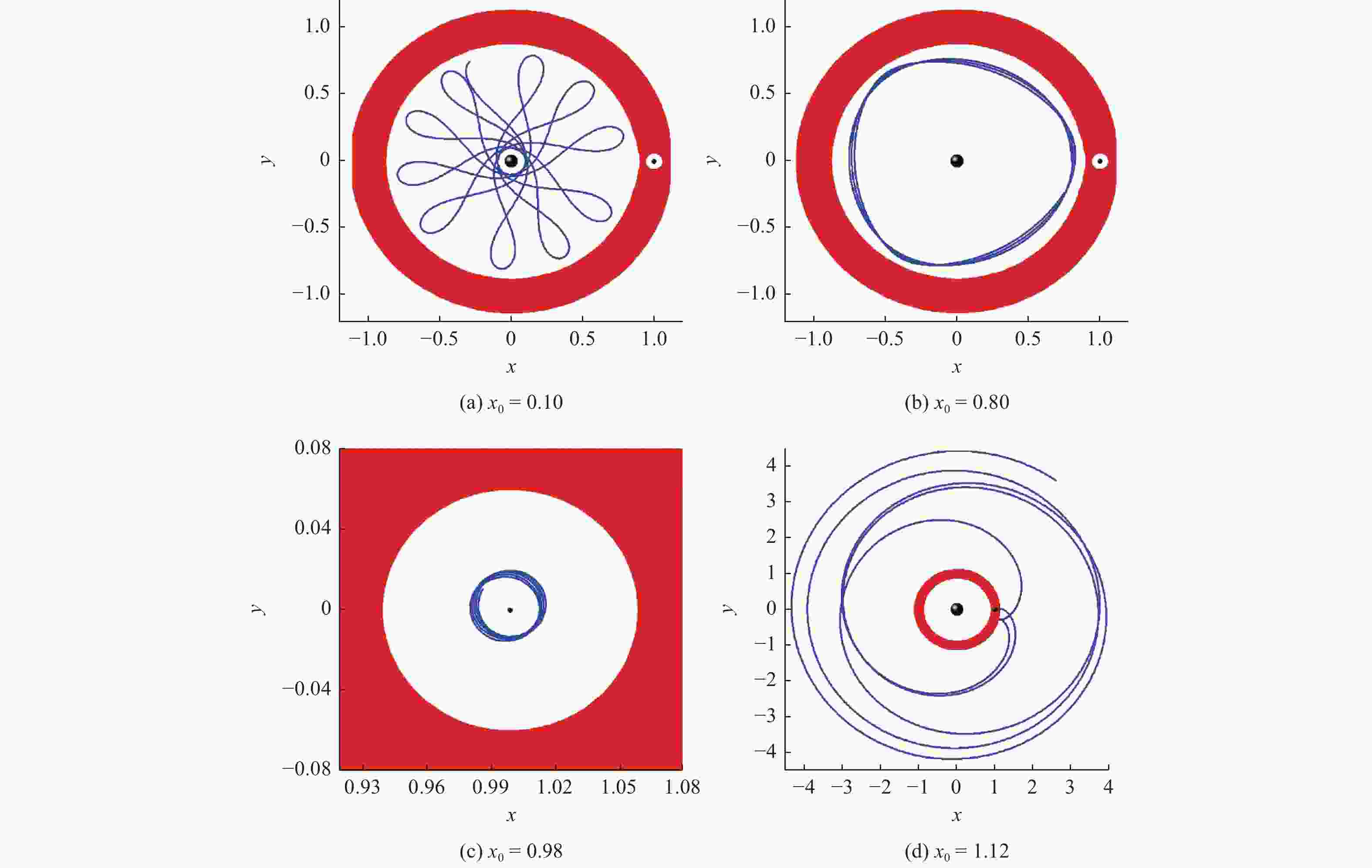
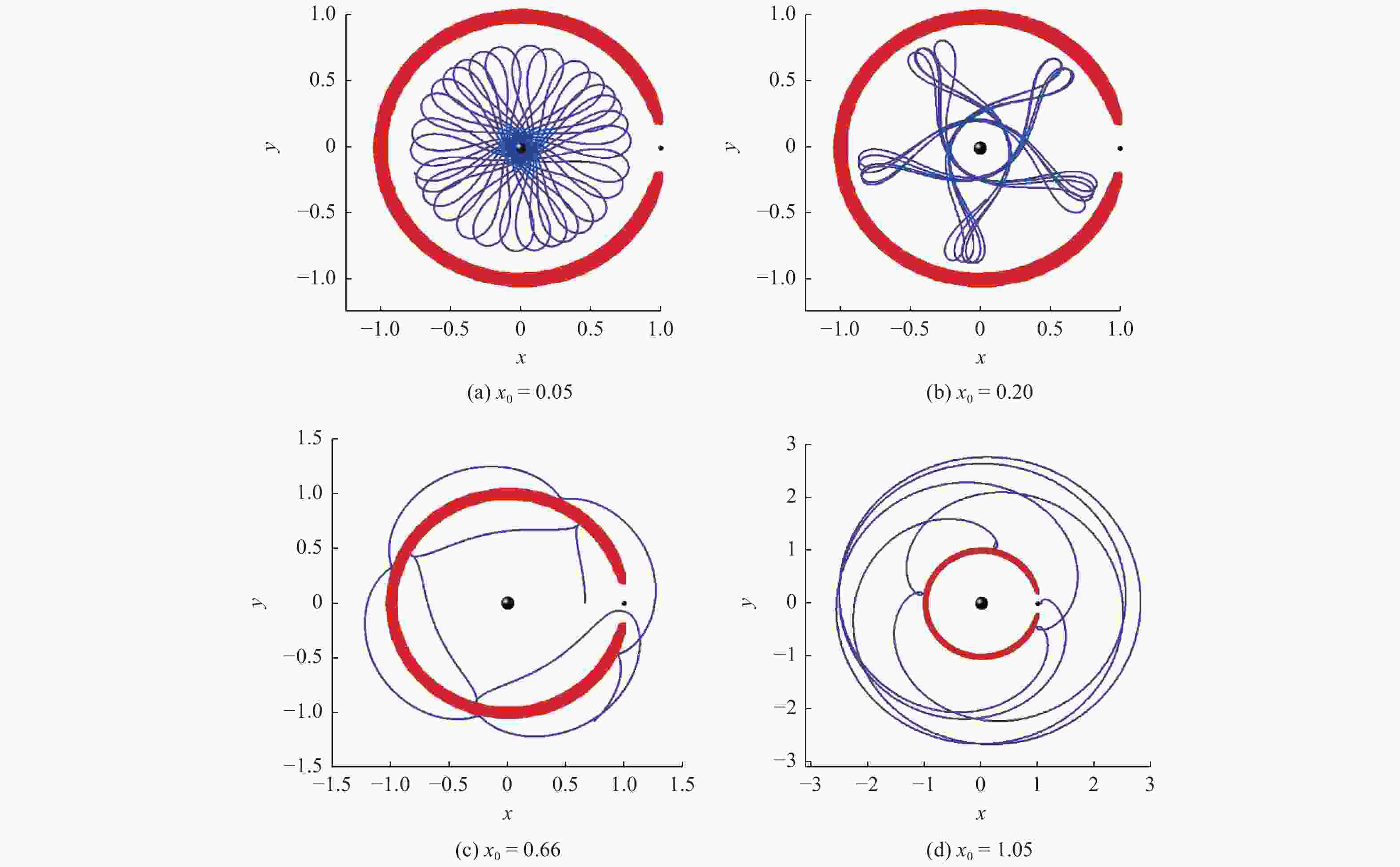
表 1 不同测试轨道的雅克比常数及初始横坐标参数
Table 1. Parameters of Jacobian constant and initial x-coordinate values for different test orbits
轨道 Cj x0 1 3.003 0.10 2 3.003 0.35 3 3.003 −1.10 4 3.003 1.05 5 3.010 0.05 6 3.010 0.20 7 3.010 0.66 8 3.010 1.05 9 3.050 0.10 10 3.050 0.80 11 3.050 0.98 12 3.050 1.12 
下载: 导出CSV
-
[1] ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Observation of gravitational waves from a binary black hole merge[J] . Physical Review Letters,2016,116(6):061102. doi: 10.1103/PhysRevLett.116.061102 [2] SZEBEHELY V, PETERS C F. Complete solution of a general problem of three body[J] . The Astronomical Journal,1967,72:876. doi: 10.1086/110355 [3] LOUSTO C O, NAKANO H. Three-body equations of motion in successive post-Newtonian approximations[J] . Classical And Quantum Gravity,2008,25(19):195019. doi: 10.1088/0264-9381/25/19/195019 [4] IMAI T, CHIBA T, ASADA H. Choreographic solution to the general-relativistic three-body problem[J] . Physical Review Letters,2007,98(20):201102. doi: 10.1103/PhysRevLett.98.201102 [5] ŠUVAKOV M, DMITRAŠINOVIĆ V. Three classes of Newtonian three-body planar periodic orbits[J] . Physical Review Letters,2013,110(11):114301. doi: 10.1103/PhysRevLett.110.114301 [6] LI D, WU X, LIANG E W. Figure-eight orbits in three post-Newtonian formulations of triple black holes[J] . Physical Review D,2021,104(4):044039. doi: 10.1103/PhysRevD.104.044039 [7] WHITTAKER E T. On periodic orbits in the restricted problem of three bodies[J] . Monthly Notices of the Royal Astronomical Society,1902,62(5):346 − 352. doi: 10.1093/mnras/62.5.346a [8] MACMILLAN W D. An integrable case in the restricted problem of three bodies[J] . The Astronomical Journal,1911,27:11 − 13. doi: 10.1086/103918 [9] 吴小婧, 曾凌川, 巩应奎. DRO计算及其在地月系中的摄动力研究[J] . 北京航空航天大学学报,2020, 46(5):883 − 892. [10] 廖新浩, 刘林. 椭圆型限制性三体问题中的轨道共振[J] . 天文学报,1988, 29(1):97 − 105. [11] 张汉清, 李言俊, 张科. 一种计算圆形限制性三体问题周期轨道的新方法[J] . 中国科学: 科学技术,2011(8):1078 − 1083. [12] 陈云龙, 伍歆. 力梯度辛方法在圆型限制性三体问题中的应用[J] . 物理学报,2013, 62(14):41 − 48. [13] 石绍伍, 马大柱. 含辐射和扁率的圆型限制性三体问题的轨道稳定性研究[J] . 天文学报,2019,60(3):36 − 46. [14] 李翔宇, 乔栋, 程潏. 三体轨道动力学研究进展[J] . 力学学报,2021,53(5):1223 − 1245. doi: 10.6052/0459-1879-20-367 [15] 周衍柏. 理论力学教程[M]. 3版. 北京: 高等教育出版社, 2009: 233-234. [16] 辛晓生, 侯锡云, 刘林. 地月系L1点的月球借力间接转移轨道设计[J] . 飞行器测控学报,2014(1):65 − 70. [17] WU X, HUANG T Y. Computation of Lyapunov exponents in general relativity[J] . Physics Letters. A,2003,313(1−2):77 − 81. doi: 10.1016/S0375-9601(03)00720-5 [18] WU X, HUANG T Y, ZHANG H. Lyapunov indices with two nearby trajectories in a curved spacetime[J] . Physical Review D: Particles, Fields, Gravitation, and Cosmology,2006,74(8):3001. doi: 10.1103/PhysRevD.74.083001 [19] PECORA L M, CARROLL T L. Synchronization in chaotic systems[J] . Physical Review Letters,1990,64:821 − 823. doi: 10.1103/PhysRevLett.64.821 [20] HUANG G Q, WU X. Dynamics of the post-Newtonian circular restricted three-body problem with compact objects[J] . Physical Review D,2014,89(12):124034. doi: 10.1103/PhysRevD.89.124034 [21] SU X N, WU X, LIU F Y. Application of the logarithmic Hamiltonian algorithm to the circular restricted three-body problem with some post-Newtonian terms[J] . Astrophysics And Space Science,2016,361(1):32. doi: 10.1007/s10509-015-2614-y -
下载:
点击查看大图
计量
- 文章访问数: 633
- HTML全文浏览量: 390
- PDF下载量: 194
- 被引次数: 0
