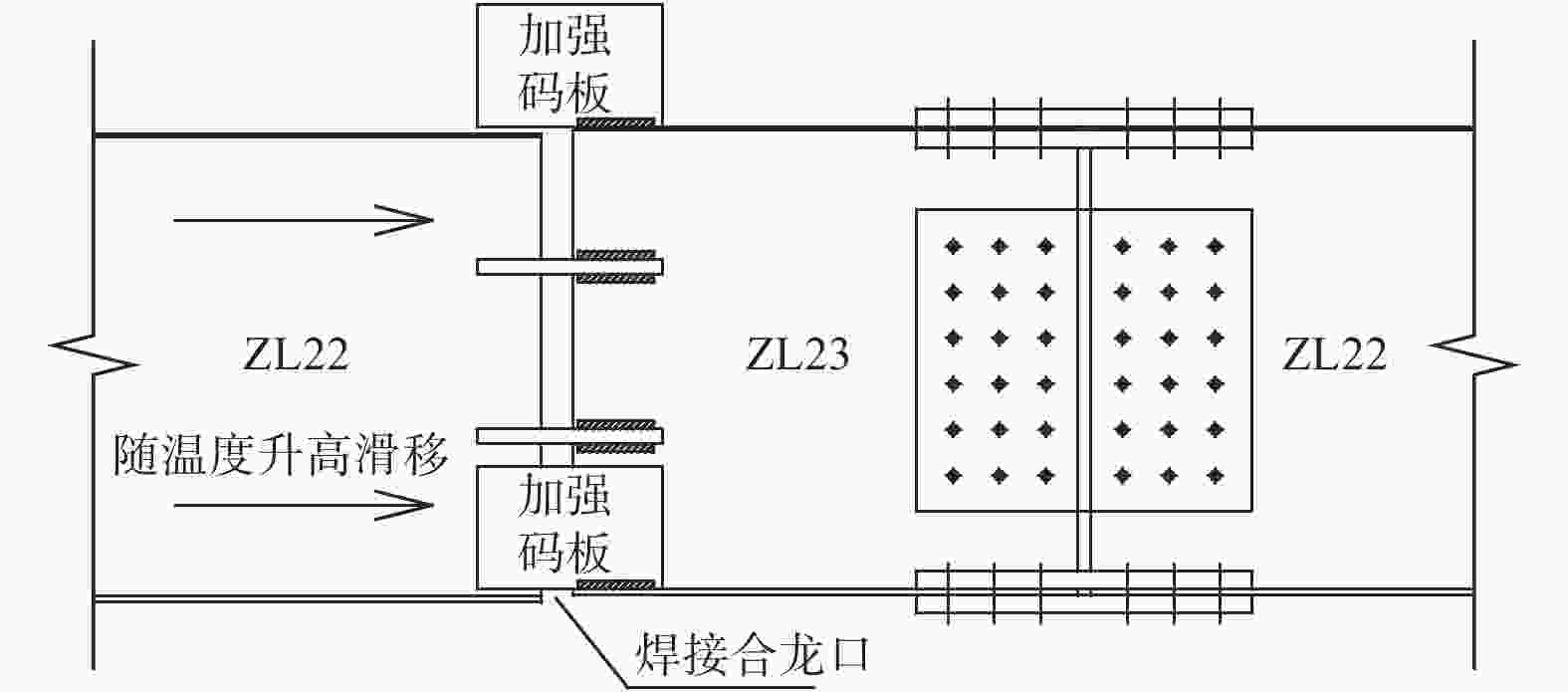
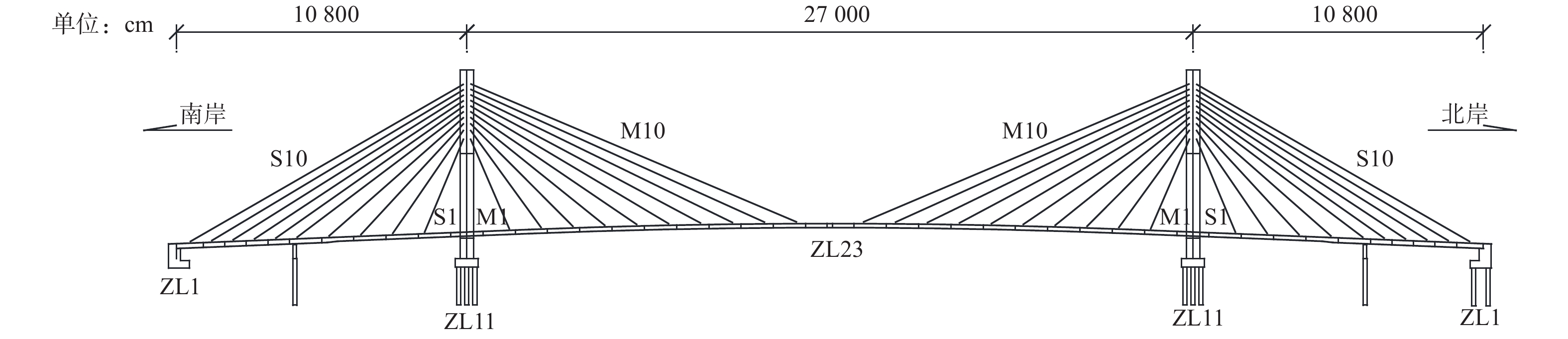
Solutions to Deviation in Closure Site of Long-Span Cable-Stayed Bridge
-
摘要: 以几内亚Boffa省一斜拉桥为例，对现场合龙过程中遇到的合龙段偏短问题进行分析. 以无应力状态法为基准，采用有限元软件进行模拟计算，并结合现场实测数据，针对性地拟定合龙方案. 计算及实测结果表明：以现有合龙段选取非低温时段进行直接合龙，对该斜拉桥合龙状态影响较小. 该方案可以确保大桥安全实现合龙，并对其他大跨斜拉桥施工中的类似合龙问题处置提供一定的参考.Abstract: Taking a cable-stayed bridge in Boffa Province, Guinea as an example, the shortness of the link section encountered during the closure process on the construction site was analyzed. Based on the unstressed state method, the finite element software was used for simulation calculation, and combined with the actual measured data on site, the closure plan was contrapuntally drawn up. The calculated and measured results show that selecting the non-low temperature period for direct linking with the existing section has little effect on the closured state of the cable-stayed bridge. This solution ensures that the bridge can be safely closured, and which provides a certain reference for the treatment of similar problems encountered in construction process of other large-span cable-stayed bridges.
-
图 1 Boffa斜拉桥立面布置示意图
Figure 1. Schematic diagram of facade layout of the Boffa cable-stayed bridge
表 1 无应力状态法计算理论参数汇总
Table 1. Summary of theoretical parameters calculated by unstressed state method
斜拉索编号 合理成桥状态 目标合龙状态 斜拉索编号 合理成桥状态 目标合龙状态 索力/kN 线形/mm 索力/kN 线形/mm 索力/kN 线形/mm 索力/kN 线形/mm S10 1155 −9 603 0 M1 401 4 162 29 S9 1028 −23 632 −39 M2 439 9 161 68 S8 1032 −27 681 −51 M3 481 11 266 118 S7 833 −22 536 −45 M4 557 10 289 170 S6 782 −11 430 −27 M5 595 8 227 224 S5 630 0 287 −5 M6 687 9 303 280 S4 575 2 255 13 M7 732 11 320 337 S3 469 −1 202 14 M8 824 13 374 388 S2 422 −7 150 3 M9 1072 9 561 425 S1 417 −8 192 −6 M10 1208 −3 559 442 注：表中线形数据为相应斜拉索对应梁段前沿位置点位标高与其成桥设计标高的差值. 
下载: 导出CSV
表 2 合龙口间距监控测量数据
Table 2. Distance monitoring data of closure section
测量时刻 平均气温/℃ 梁体温度/℃ 合龙口间距/m 左侧 右侧 6:00 22.1 22.4 2.202 2.210 8:00 23.7 24.0 2.190 2.197 10:00 25.3 26.8 2.173 2.181 11:00 27.4 32.5 2.168 2.175 12:00 30.2 35.9 2.135 2.143 14:30 39.2 46.7 2.112 2.120 17:00 32.3 38.8 2.140 2.151 18:00 27.7 32.4 2.162 2.173 19:00 24.6 28.6 2.195 2.204 20:00 23.4 25.1 2.204 2.217 23:00 22.2 23.4 2.208 2.218
下载: 导出CSV
表 3 实际合龙状态参数偏差
Table 3. Parameter deviation of actual linked state
斜拉索编号 计算合龙状态 实际方案合龙状态 偏差 索力/kN 线形/mm 索力/kN 线形/mm 索力/% 线形/mm 2#塔中心 — 0 — 4 — 4 南M1 162 29 165 39 2.2 10 南M2 161 68 166 87 2.9 19 南M3 266 118 255 105 −4.3 −13 南M4 289 170 299 169 3.5 −1 南M5 227 224 240 244 5.9 21 南M6 303 280 303 258 −0.1 −22 南M7 320 337 303 353 −5.3 16 南M8 374 388 354 388 −5.4 −1 南M9 561 425 544 427 −3.1 2 南M10 559 442 571 461 2.1 19 跨中 — 444 — 471 — 27 北M10 559 442 589 455 5.3 13 北M9 561 425 529 419 −5.7 −6 北M8 374 388 401 379 7.1 −9 北M7 320 337 308 363 −3.7 26 北M6 303 280 319 291 5.1 11 北M5 227 224 215 249 −5.2 25 北M4 289 170 280 193 −3.1 23 北M3 266 118 253 117 −4.9 −1 北M2 161 68 172 89 6.6 21 北M1 162 29 173 20 6.8 −9 3#塔中心 — 0 — −2 — −2
下载: 导出CSV
-
[1] 刘亚明, 马晓谦. 基于无应力状态法的双塔斜拉桥合理施工状态研究[J] . 公路交通科技(应用技术版),2017,13(7):306 − 307. [2] 楚发强. 独塔不对称斜拉桥合龙方案的选择与优化[J] . 黑龙江交通科技,2018,41(1):90 − 91. doi: 10.3969/j.issn.1008-3383.2018.01.047 [3] 乔永和, 李盼盼, 古培峰. 涪江五桥独塔斜拉桥主梁合龙段施工技术[J] . 筑路机械与施工机械化,2017,34(6):86 − 90. doi: 10.3969/j.issn.1000-033X.2017.06.016 [4] 包龙生, 肖成忠, 于玲, 等. 大跨度混凝土连续梁桥施工监控参数敏感性分析方法[J] . 沈阳建筑大学学报(自然科学版),2012,28(6):1068 − 1073. [5] 王世界, 于太乐, 许斐, 等. 某异形拱桥施工监控参数敏感性分析[J] . 上海工程技术大学学报,2014,28(3):215 − 220. doi: 10.3969/j.issn.1009-444X.2014.03.006 [6] 谢小辉, 郑兴贵, 杨志军. 基于无应力状态法的斜拉桥合理施工状态确定[J] . 四川建筑科学研究,2016,42(5):133 − 136. doi: 10.3969/j.issn.1008-1933.2016.05.030 [7] 邓小伟. 施工方案中途改变的独塔斜拉桥变更设计与结构分析[J] . 城市道桥与防洪,2018(8):156 − 160, 199. [8] 黎磊. 双塔双索面组合梁斜拉桥合龙段施工方案及关键技术分析[J] . 智能城市,2020,6(6):189 − 190. [9] 王世界, 王梓鉴, 于太乐. 基于伸长量的影响矩阵法在提篮拱桥调索中的应用[J] . 城市道桥与防洪,2019(11):133 − 137, 17. -
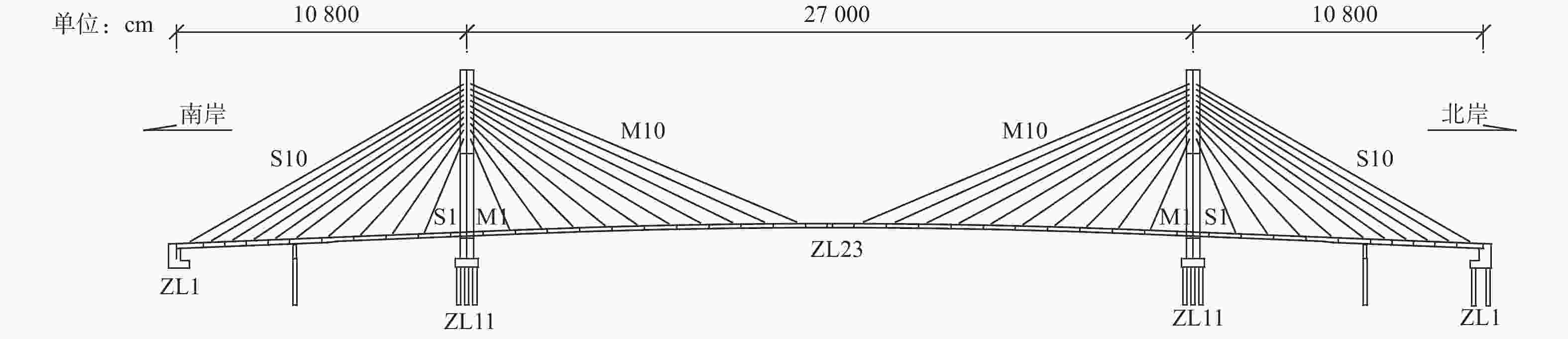
下载:
点击查看大图
计量
- 文章访问数: 215
- HTML全文浏览量: 149
- PDF下载量: 86
- 被引次数: 0
