考虑惯性力矩与剪切变形的曲梁面内自由振动微分方程的建立

张智超; 宋郁民

考虑惯性力矩与剪切变形的曲梁面内自由振动微分方程的建立

张智超,
宋郁民^,

上海工程技术大学城市轨道交通学院, 上海201620

详细信息

作者简介:
张智超（1997−），男，在读硕士，研究方向为桥梁结构设计与分析. E-mail:1771028705@qq.com

通讯作者:
宋郁民（1976−），男，副教授，博士，研究方向为桥梁结构分析和结构动力学. E-mail:song-yumin@qq.com

中图分类号: U441
计量
- 文章访问数: 665
- HTML全文浏览量: 391
- PDF下载量: 189
- 被引次数: 3
出版历程
- 收稿日期: 2021-05-23
- 刊出日期: 2022-02-23

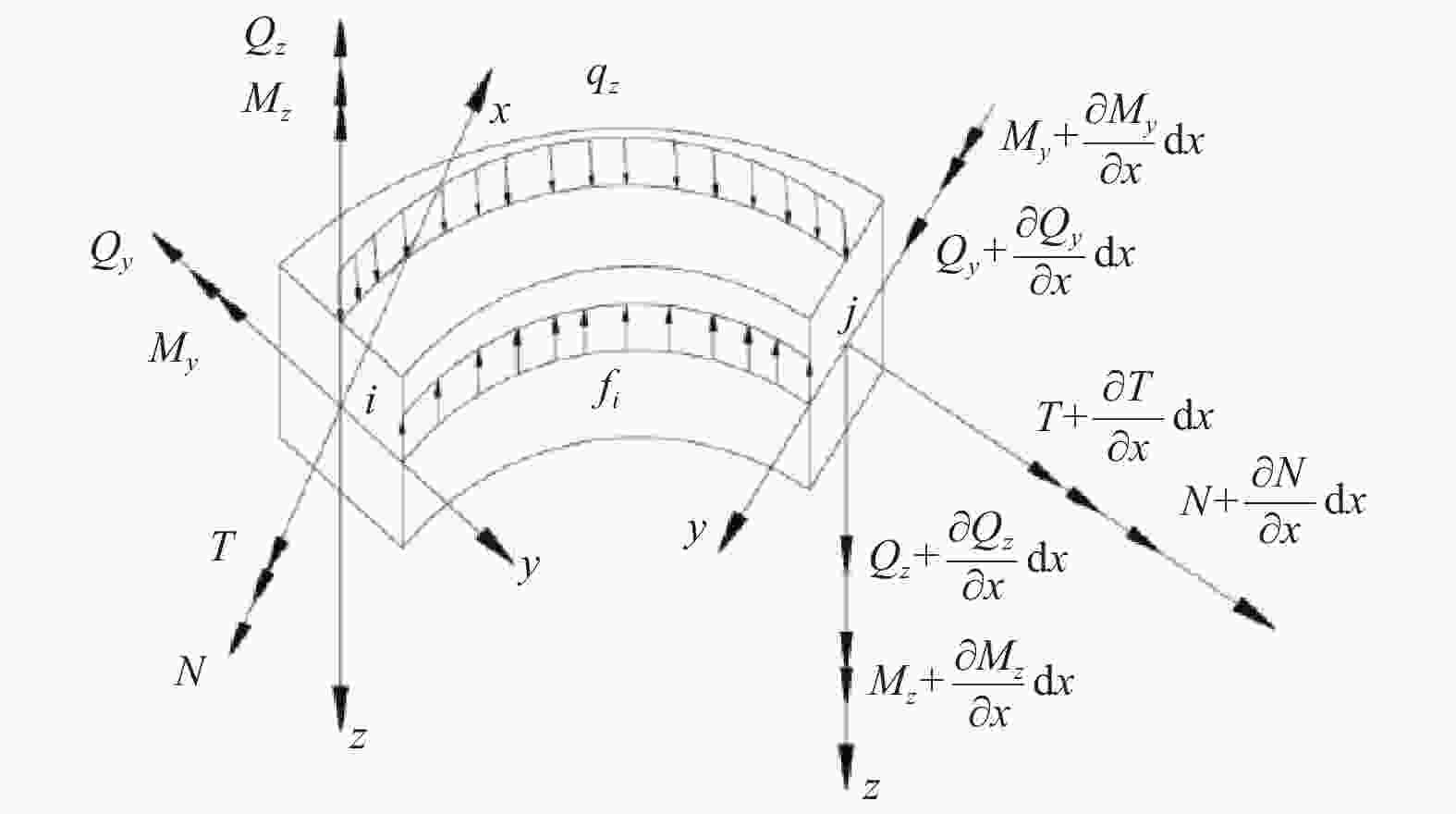
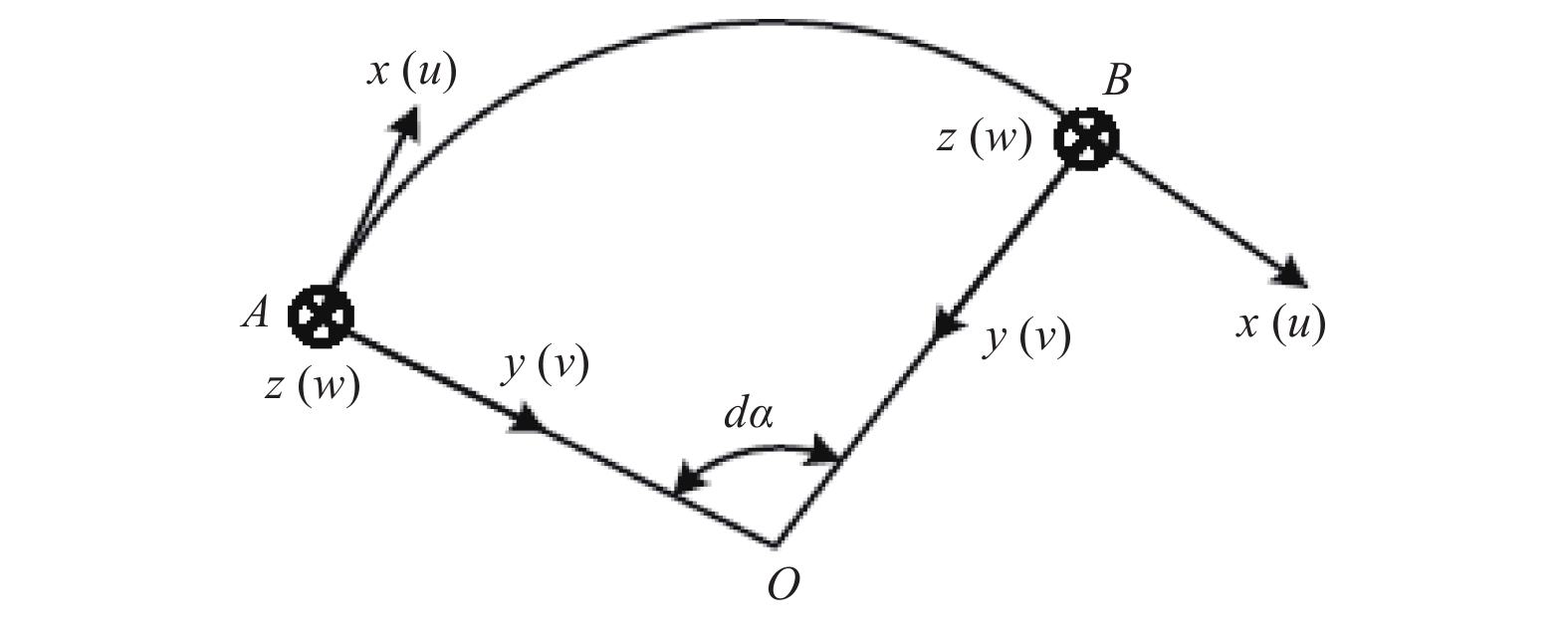
Establishment of differential equation of in-plane free vibration of curved beams under MOI and shear deformation

ZHANG Zhichao,
SONG Yumin^,

School of Urban Rail Transportation, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

摘要: 振动微分方程的推导与建立是结构动力分析的关键. 依据Timoshenko梁理论，计入惯性力矩与剪切变形的影响，通过联立几何变形协调方程与内力平衡方程，推导建立曲梁面内横向弯曲自由振动微分方程与曲梁面内轴向自由振动微分方程. 研究结果为曲梁动力学研究提供一定的理论基础.
- 曲梁 /
- 惯性力矩 /
- 剪切变形 /
- 振动微分方程 /
- Timoshenko梁
Abstract: The derivation and establishment of vibration differential equation are the key to the structural dynamic analysis. The moment of inertia (MOI) and shear deformation were taken into account, the differential equations of in-plane free vibration about lateral bending and axial deformation of curved beams were derived and established by combining geometric equations and the internal force equilibrium according to the theory of Timoshenko beam. The research results can provide a theoretical basis for dynamic study on the curved beams.
- curved beams /
- moment of inertia (MOI) /
- shear deformation /
- vibration differential equation /
- Timoshenko beam

HTML全文

曲梁在土木、机械、交通运输等领域均有应用，因此曲梁的力学特性近年来被学者们广泛研究. 针对曲梁的静力学研究，目前已发展得较为成熟. 同时，近几十年来工程中的动力学计算逐渐受到人们重视，因此学者们开始关注曲梁的动力特性研究^[1-4].

在直梁条件下，根据Timoshenko理论目前已建立系统的考虑惯性力矩与剪切变形影响下的振动微分方程得知，对于细长梁而言，惯性力矩与剪切变形的影响可以忽略不计. 然而对于深梁，即高跨比较大的梁而言，忽略二者则会导致计算结果误差较大. 考虑到直梁条件下建立的计入惯性力矩与剪切变形影响下的振动微分方程，而曲梁是直梁的一般情况，因此本研究将二者影响考虑至曲梁振动微分方程的建立之中.

针对曲梁动力学研究，宋郁民等^[5-6]在Euler梁模型下，即不考虑惯性力矩与剪切变形条件下的圆弧曲梁振动微分方程的推导，同时采用假定振型函数的方法对上述微分方程进行求解. 基于上述研究，本研究在已有的Euler梁曲梁模型下依据Timoshenko理论^[7]，计入惯性力矩与剪切变形，建立曲梁面内自由振动微分方程，推导并整理完成曲梁面内横向弯曲自由振动微分方程、面内轴向自由振动微分方程. 方程未计入阻尼影响，且具有一般性，具体边界条件随梁的固定形式不同而不同.

参考直梁条件下振动微分方程，曲梁振动微分方程推导需建立几何变形协调方程与内力平衡方程，通过结构变形与内力关系将二者联立. 本研究中，符号定义如下： $m$ 为单位长度的质量； ${J_m}$ 为转动惯量； $\rho$ 为单位体积的质量； $J$ 为截面极惯性矩； $E$ 为杨氏模量； $I$ 为截面惯性矩.

1. 坐标系及正方向规定

1.1 坐标系规定

曲梁平面图如图1所示. 取圆弧微段AB，其圆心角为 $d\alpha$ ，坐标系采用三维空间直角坐标系. $x$ 轴为圆弧切线方向，对应位移为 $u$ ； $y$ 轴为指向圆心圆弧法线方向，对应位移为 $v$ ； $z$ 轴为铅垂向下圆弧法线方向，对应位移为 $w$ .

图 1 曲梁平面图

Figure 1. Plan of the curved beam

下载: 全尺寸图片幻灯片

1.2 正方向规定

参考材料力学，对内力与变形正方向做如下规定：

1）轴力与轴向变形以受拉为正；

2）转矩与扭转角采用右手法则，即右手拇指指向离开截面时，四指方向为正；

3）剪力以所选梁段任意一点的矩为顺时针转向时为正，弯矩以使曲梁内侧（面外变形）、下侧（面外变形）受拉为正；

4）与正向弯矩使曲梁变形方向一致，面内挠度（ $v$ ）以指向圆心方向为正，面外挠度（ $w$ ）以垂直向下为正；

5）与正向弯矩使曲梁变形方向一致，曲率平面内弯曲应变（绕 $z$ 轴的 ${\kappa _z}$ ）以使曲梁内侧受拉为正，面外弯曲应变（绕 $y$ 轴的 ${\kappa _y}$ ）以使曲梁下侧受拉为正.

2. 曲梁几何变形协调方程

2.1 不计剪切变形曲梁几何变形协调方程

不计剪切变形曲梁几何变形协调方程^[8]为

$\left\{ {\begin{array}{l} {{\varepsilon _x} = \dfrac{{{\rm{d}}u}}{{{\rm{d}}x}} - \dfrac{v}{R}}\\ {{\kappa _z} = \dfrac{{{{\rm{d}}^2}v}}{{{\rm{d}}{x^2}}} + \dfrac{v}{{{R^2}}}}\\ {{\kappa _y} = \dfrac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}} - \dfrac{\varphi }{R}}\\ {{\kappa _x} = \dfrac{{{\rm{d}}\varphi }}{{{\rm{d}}x}} + \dfrac{1}{R}\dfrac{{{\rm{d}}w}}{{{\rm{d}}x}}} \end{array}} \right.$

(1)

式中：ε_x为面内—轴向应变；κ_z为面内—绕z轴曲率（曲梁面内横向弯曲）；κ_y为面外—绕y轴曲率（曲梁面外横向弯曲）；κ_x为面外—绕x轴曲率（曲梁面外纵向扭转）；φ为扭转角.

2.2 计入剪切变形曲梁几何变形协调方程

Euler梁中梁截面转角 $\theta$ 与挠曲线倾角 $\dfrac{{{\rm{\partial }} y}}{{{\rm{\partial }} x}}$ 相等. 而在Timoshenko梁中，倾角 $\dfrac{{{\rm{\partial }} y}}{{{\rm{\partial }} x}}$ 需剔除剪切变形剪切角 $\gamma$ 后与截面弯曲转角 $\theta$ 相等，几者关系为

$\gamma = \frac{{{\rm{\partial }} y}}{{{\rm{\partial }} x}} - \theta$

(2)

$Q = \frac{{GA}}{k}\gamma$

(3)

式中： $\gamma$ 为剪切角； $y$ 为弯曲挠度； $\dfrac{{\partial y}}{{\partial x}}$ 为挠曲线倾角； $\theta$ 为截面弯曲转角； $G$ 为剪切模量； $A$ 为截面面积； $k$ 为考虑截面上剪应力分布不均匀的修正系数. 因式(1)不再适用，根据式(2)对式(1)进行调整，得到计入剪切变形曲梁几何变形协调方程为

$\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \dfrac{{{\rm{d}}u}}{{{\rm{d}}x}} - \dfrac{v}{R}}\\ \begin{array}{l} {\kappa _z} = \dfrac{{{\rm{d}}{\theta _z}}}{{{\rm{d}}x}} + \dfrac{v}{{{R^2}}}{\rm{ = }}\dfrac{{\rm{d}}}{{{\rm{d}}x}}\left( {\dfrac{{{\rm{d}}v}}{{{\rm{d}}x}} - {\gamma _y}} \right) + \dfrac{v}{{{R^2}}} = \\ \;\;\;\;\;\;\;\;\dfrac{{{{\rm{d}}^2}v}}{{{\rm{d}}{x^2}}} - \dfrac{{{\rm{d}}{\gamma _y}}}{{{\rm{d}}x}} + \dfrac{v}{{{R^2}}} \end{array}\\ \begin{array}{l} {\kappa _y} = \dfrac{{{\rm{d}}{\theta _y}}}{{{\rm{d}}x}} - \dfrac{\varphi }{R} = \dfrac{{\rm{d}}}{{{\rm{d}}x}}\left( {\dfrac{{{\rm{d}}w}}{{{\rm{d}}x}} - {\gamma _z}} \right) - \dfrac{\varphi }{R} = \\ \;\;\;\;\;\;\;\;\dfrac{{{\rm{d}}{w^2}}}{{{\rm{d}}{x^2}}} - \dfrac{{{\rm{d}}{\gamma _z}}}{{{\rm{d}}x}} - \dfrac{\varphi }{R} \end{array}\\ {{\kappa _x} = \dfrac{{{\rm{d}}\varphi }}{{{\rm{d}}x}} + \dfrac{{{\theta _y}}}{R}{\rm{ = }}\dfrac{{{\rm{d}}\varphi }}{{{\rm{dx}}}}{\rm{ + }}\dfrac{{\rm{1}}}{{\rm{R}}}\left( {\dfrac{{{\rm{dw}}}}{{{\rm{dx}}}}{\rm{ - }}{\gamma _{\rm{z}}}} \right)} \end{array}} \right.$

(4)

式中： ${\gamma _y}$ 为 $y$ 方向剪切角， ${\gamma _z}$ 为 $z$ 方向剪切角. 根据式(2)可得y轴、z轴方向剪力为

$\begin{array}{*{20}{c}} {{Q_y} = \dfrac{{GA}}{k}{\gamma _y}}&{{Q_z} = \dfrac{{GA}}{k}{\gamma _z}}\text{.} \end{array}$

观察式(4)可得，计入剪切变形对面内与面外弯曲变形方程造成影响. 观察式面外—绕x轴曲率，倘若为直梁，则计入剪切变形并不会影响扭转变形方程，由于曲梁中弯扭耦合（即弯曲与扭转变形相互影响），因此计入剪切变形后间接影响了扭转变形几何协调方程.

3. 曲梁内力平衡方程

曲梁微段内力图如图2所示，圆心角为 $d\alpha$ .

图 2 曲梁微段内力图

Figure 2. Graph of curved beam segment internal force

下载: 全尺寸图片幻灯片

在 $x$ 轴与 $y$ 轴方向，微段两端的内力均不在同一3维坐标系内. 因此需统一坐标系，即将左端内力进行坐标变换，再建立内力平衡方程. 坐标变换矩阵S为

${\boldsymbol {S}} =\left[ {\begin{array}{*{20}{c}} {\cos d\alpha }&{\sin d\alpha }&0&{}&{}&{} \\ { - \sin d\alpha }&{\cos d\alpha }&0&{}&0&{} \\ 0&0&1&{}&{}&{} \\ {}&{}&{}&{\cos d\alpha }&{\sin d\alpha }&0 \\ {}&0&{}&{ - \sin d\alpha }&{\cos d\alpha }&0 \\ {}&{}&{}&0&0&1 \end{array}} \right]$

(5)

通过上述矩阵将微段左端点内力进行坐标变换，使其与右端点内力坐标系相统一. 具体步骤为左端内力行向量右乘坐标变换矩阵，由于曲梁微段圆心角 $d\alpha$ 极小，因此在计算时有 $\cos d\alpha \approx 1$ ， $\sin d\alpha \approx d\alpha$ ，可得坐标变换后内力行向量为

$\qquad\qquad\qquad\qquad\qquad\;\; \begin{array}{c} {\left[\begin{array}{c}N\\ {Q}_{y}\\ {Q}_{z}\\ T\\ {M}_{y}\\ {M}_{z}\end{array}\right]}^{{\rm {T}}}·\left[\begin{array}{cccccc}1& d\alpha & 0& & & \\ -d\alpha & 1& 0& & {\bf{0}}& \\ 0& 0& 1& & & \\ & & & 1& d\alpha & 0\\ & {\bf{0}}& & -d\alpha & 1& 0\\ & & & 0& 0& 1\end{array}\right]\text={\left[\begin{array}{c}N\text+{Q}_{y}\cdot d\alpha \\ -N\cdot d\alpha +{Q}_{y}\\ {Q}_{z}\\ T+{M}_{y}\cdot d\alpha \\ -T\cdot d\alpha +{M}_{y}\\ {M}_{z}\end{array}\right]}^{{\rm{T}}} \end{array}$

(6)

式中： $T$ 为绕x轴扭转扭矩； ${M_y}$ 为绕y轴弯曲弯矩（面外横向弯曲弯矩）； ${M_z}$ 为绕z轴弯曲弯矩（面内横向弯曲弯矩）；N为x轴方向轴力.

根据坐标变换后内力行向量与微段右端内力列出曲梁内力平衡方程，其中，惯性力与惯性力矩方向同结构动力学保持一致， $\dfrac{{d\alpha }}{{dx}} = \dfrac{1}{R}$ . 根据是否计入惯性力矩得出如下结果.

1) 不计惯性力矩曲梁内力平衡方程

$\begin{split} & \sum X = 0 {\text{时，有}} \qquad \\ &- (N + {Q_y} \cdot d\alpha ) + \left(N + \frac{{{\rm{\partial }} N}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - m\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$- \frac{{{Q_y}}}{R} + \frac{{{\rm{\partial }} N}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {t^2}}} = 0$

式中：m为单位长度的质量.

$\begin{split} & \sum Y = 0{\text{时，有}}\qquad\\ &- ( - N \cdot d\alpha + {Q_y}) + \left({Q_y} + \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{N}{R} + \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} = 0$

$\begin{split} &\sum Z = 0{\text{时，有}} \qquad \\ & - {Q_z} + \left({Q_z} + \frac{{{\rm{\partial }} {Q_z}}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - m\frac{{{{\rm{\partial }} ^2}w}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{{{\rm{\partial }} {Q_z}}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}w}}{{{\rm{\partial }} {t^2}}} = 0$

$\begin{split} &{\sum M _x} = 0 \;{\text{时，有}} \qquad \\ &- (T + {M_y} \cdot d\alpha ) + \left(T + \frac{{{\rm{\partial }} T}}{{{\rm{\partial }} x}}{\rm{d}}x\right) -{J_m}\frac{{{{\rm{\partial }} ^2}\varphi }}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{{{\rm{\partial }} T}}{{{\rm{\partial }} x}} - \frac{{{M_y}}}{R} - {J_m}\frac{{{{\rm{\partial }} ^2}\varphi }}{{{\rm{\partial }} {t^2}}} = 0$

式中：J_m为转动惯量.

化简得

$\frac{{{\rm{\partial }} {M_y}}}{{{\rm{\partial }} x}} - {Q_z} + \frac{T}{R} = 0$

化简得

$\frac{{{\rm{\partial }} {M_z}}}{{{\rm{\partial }} x}} - {Q_y} = 0$

2) 计入惯性力矩曲梁内力平衡方程

$\begin{split} & \sum X = 0\; {\text{时，有}} \qquad \\ &- (N + {Q_y} \cdot d\alpha ) + \left( N + \frac{{{\rm{\partial }} N}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - m\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$- \frac{{{Q_y}}}{R} + \frac{{{\rm{\partial }} N}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {t^2}}} = 0$

$\begin{split} & \sum Y = 0 \;{\text{时，有}} \qquad \\ & - ( - N \cdot d\alpha + {Q_y}) + \left( {Q_y} + \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{N}{R} + \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} = 0$

$\begin{split} & \sum Z = 0 {\text{时，有}} \qquad \\ & - {Q_z} + \left({Q_z} + \frac{{{\rm{\partial }} {Q_z}}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - m\frac{{{{\rm{\partial }} ^2}w}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{{{\rm{\partial }} {Q_z}}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}w}}{{{\rm{\partial }} {t^2}}} = 0$

$\begin{split} & {\sum M _x} = 0\;{\text{时，有}} \qquad \\ & - (T + {M_y} \cdot d\alpha ) + \left(T + \frac{{{\rm{\partial }} T}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - {J_m}\frac{{{{\rm{\partial }} ^2}\varphi }}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{{{\rm{\partial }} T}}{{{\rm{\partial }} x}} - \frac{{{M_y}}}{R} - {J_m}\frac{{{{\rm{\partial }} ^2}\varphi }}{{{\rm{\partial }} {t^2}}} = 0$

$\begin{split} &{\sum M _y} = 0 \;{\text{时，有}} \qquad \\ & - \left( - T \cdot d\alpha + {M_y}\right) + \left({M_y} + \frac{{{\rm{\partial }} {M_y}}}{{{\rm{\partial }} x}}{\rm{d}}x\right) -\\ & \qquad \qquad \;\;\; {Q_z} \cdot {\rm{d}}x + \rho {I_y}\frac{{{{\rm{\partial }} ^2}{\theta _y}}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{{{\rm{\partial }} {M_y}}}{{{\rm{\partial }} x}} - {Q_z} + \frac{T}{R} + \rho {I_y}\frac{{{{\rm{\partial }} ^2}{\theta _y}}}{{{\rm{\partial }} {t^2}}} = 0$

式中：ρ为单位体积的质量.

$\begin{split}& {\sum M _z} = 0\; {\text{时，有}} \qquad \\ & - {M_z} + \left( {M_z} + \frac{{{\rm{\partial }} {M_z}}}{{{\rm{\partial }} x}}{\rm{d}}x\right) - {Q_y} \cdot {\rm{d}}x + \\ &\qquad \qquad \;\;\;\;\; \rho {I_z}\frac{{{{\rm{\partial }} ^2}{\theta _z}}}{{{\rm{\partial }} {t^2}}} \cdot {\rm{d}}x = 0 \end{split}$

化简得

$\frac{{{\rm{\partial }} {M_z}}}{{{\rm{\partial }} x}} - {Q_y} + \rho {I_z}\frac{{{{\rm{\partial }} ^2}{\theta _z}}}{{{\rm{\partial }} {t^2}}} = 0$

4. 曲梁面内振动微分方程推导

4.1 面内横向弯曲振动微分方程推导

考虑惯性力矩与剪切变形时建立面内横向弯曲振动微分方程，需联立内力平衡方程 $\sum Y = 0$ ， ${\sum M _z} = 0$ ，可得

$\frac{N}{R} + \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} = 0$

(7)

$\frac{{{\rm{\partial }} {M_z}}}{{{\rm{\partial }} x}} - {Q_y} + \rho {I_z}\frac{{{{\rm{\partial }} ^2}{\theta _z}}}{{{\rm{\partial }} {t^2}}} = 0$

(8)

材料力学中内力与变形关系为

$N = EA{\varepsilon _x}$

(9)

${M_z} = - E{I_z}{\kappa _z}$

(10)

式中：E为杨氏模量.

将式(4)代入上式（为方便后续计算，几何变形协调方程取至弯曲转角 $\theta$ ），得

$N = EA\left(\frac{{{\rm{d}}u}}{{{\rm{d}}x}} - \frac{v}{R}\right)$

(11)

${M_z} = - E{I_z}\left(\frac{{{\rm{d}}{\theta _z}}}{{{\rm{d}}x}} + \frac{v}{{{R^2}}}\right)$

(12)

联立方程需剪切角 $\gamma$ 、挠度 $y$ （此小节挠度为 $v$ ）、截面弯曲转角 $\theta$ 三者关系式及剪切角 $\gamma$ 与剪力 $Q$ 关系式. 将式(3)代入式(2)后，两端对 $x$ 求一阶导数，得

$\frac{k}{{GA}} \cdot \frac{{{\rm{\partial }} Q}}{{{\rm{\partial }} x}} = \frac{{{{\rm{\partial }} ^2}y}}{{{\rm{\partial }} {x^2}}} - \frac{{{\rm{\partial }} \theta }}{{{\rm{\partial }} x}}$

(13)

挠度为 $v$ ，转角为 ${\theta _z}$ ，剪力为 ${Q_y}$ 时，经整理可得

$\frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}} = \frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \frac{k}{{GA}} \cdot \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}}$

(14)

将内力平衡方程即式(7)代入式(14)，可得

$\frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}} = \frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \frac{k}{{GA}} \cdot \left(m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \frac{N}{R}\right)$

(15)

将式(11)代入式(15)，可得

$\begin{split}& \frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}} = \frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \frac{k}{{GA}} \cdot \\& \left(m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \frac{{EA}}{R} \cdot \frac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} + \frac{{EA}}{{{R^2}}} \cdot v\right) \end{split}$

(16)

式(8)两端对 $x$ 求一阶导数，可得

$\frac{{{{\rm{\partial }} ^2}{M_z}}}{{{\rm{\partial }} {x^2}}} - \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}} + \rho {I_z}\frac{{{{\rm{\partial }} ^2}}}{{{\rm{\partial }} {t^2}}}\left(\frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}}\right) = 0$

(17)

将式(7)代入式(17)，得

$\frac{{{{\rm{\partial }} ^2}{M_z}}}{{{\rm{\partial }} {x^2}}} - \left( {m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \frac{N}{R}} \right) + \rho {I_z}\frac{{{{\rm{\partial }} ^2}}}{{{\rm{\partial }} {t^2}}}\left(\frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}}\right) = 0$

(18)

将式(11)、式(12)代入式(18)，可得

$\begin{split} & \frac{{{{\rm{\partial }} ^2}}}{{{\rm{\partial }} {x^2}}}\left[ { - E{I_z}\left( \frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}} + \frac{v}{{{R^2}}}\right)} \right] -\\ &\qquad \left\{ {m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \frac{1}{R}\left[ {EA\left( \frac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} - \frac{v}{R}\right)} \right]} \right\} + \\& \qquad \rho {I_z}\frac{{{{\rm{\partial }} ^2}}}{{{\rm{\partial }} {t^2}}}\left( \frac{{{\rm{\partial }} {\theta _z}}}{{{\rm{\partial }} x}}\right) = 0 \end{split}$

(19)

将式(16)代入式(19)，可得

$\begin{split} & \dfrac{{{{\rm{\partial }} ^2}}}{{{\rm{\partial }} {x^2}}}\Biggl\{{18} { - E{I_z}\Biggl[{17} {\dfrac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \dfrac{k}{{GA}} \cdot \Biggl({16} m\dfrac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \dfrac{{EA}}{R} \cdot \dfrac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} + } } \\ &\quad { { {\dfrac{{EA}}{{{R^2}}} \cdot v} \Biggl){16} + \dfrac{v}{{{R^2}}}} \Bigggr]{17} } \Biggl\}{18} - \left[{m\dfrac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \dfrac{1}{R}{EA\left(\dfrac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} - \dfrac{v}{R}\right)} } \right]+ \\ &\quad \rho {I_z}\dfrac{{{{\rm{\partial }} ^2}}}{{{\rm{\partial }} {t^2}}}\left[ \dfrac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \dfrac{k}{{GA}} \cdot\right.\\ &\quad \left.\left(m\dfrac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \dfrac{{EA}}{R} \cdot \dfrac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} + \dfrac{{EA}}{{{R^2}}} \cdot v\right) \right] = 0\\[-15pt] \end{split}$

(20)

整理得曲梁面内横向弯曲振动微分方程为

$\begin{split} E{I_z}\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^4}}} &+ m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \rho {I_z}\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^2}{\rm{\partial }} {t^2}}} - \frac{{E{I_z}k}}{{GA}}m\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^2}{\rm{\partial }} {t^2}}} +\\ &\frac{{\rho {I_z}k}}{{GA}}m\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {t^4}}} - \frac{{EA}}{R} \cdot \frac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} + \frac{{EA}}{{{R^2}}} \cdot v +\\ &\frac{{E{I_z}}}{{{R^2}}} \cdot \frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} + \frac{{Ek}}{{GR}}\left( {E{I_z}\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} {x^3}}} - \rho {I_z}\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} x{\rm{\partial }} {t^2}}}} \right) -\\ &\frac{{Ek}}{{G{R^2}}}\left( {E{I_z}\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \rho {I_z}v} \right) =0 \\[-18pt] \end{split}$

(21)

式中：多项式 $E{I_z}\dfrac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^4}}} + m\dfrac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}}$ 为Euler梁条件下基本情况；多项式 $- \rho {I_z}\dfrac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^2}{\rm{\partial }} {t^2}}}$ 为Timoshenko梁条件下惯性力矩影响项；多项式 $- \dfrac{{E{I_z}k}}{{GA}}m\dfrac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^2}{\rm{\partial }} {t^2}}}$ 为Timoshenko梁条件下剪切变形影响项；多项式 $\dfrac{{\rho {I_z}k}}{{GA}}m\dfrac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {t^4}}}$ 为剪切变形与惯性力矩耦合影响项；多项式 $- \dfrac{{EA}}{R} \cdot \dfrac{{\partial u}}{{\partial x}} + \dfrac{{EA}}{{{R^2}}} \cdot v + \dfrac{{E{I_z}}}{{{R^2}}} \cdot \dfrac{{{\partial ^2}v}}{{\partial {x^2}}}$ 为曲梁面内轴弯耦合影响项；多项式 $\dfrac{{Ek}}{{GR}}\left( {E{I_z}\dfrac{{{\partial ^3}u}}{{\partial {x^3}}} - \rho {I_z}\dfrac{{{\partial ^3}u}}{{\partial x\partial {t^2}}}} \right) - \dfrac{{Ek}}{{G{R^2}}}\cdot$ $\left( {E{I_z}\dfrac{{{\partial ^2}v}}{{\partial {x^2}}} - } \right.{\rho {I_z}v} \Biggr)$ 为曲梁影响项，受剪切变形与惯性力矩共同影响.

4.2 面内轴向振动微分方程推导

建立面内轴向振动微分方程，需联立内力平衡方程 $\sum X = 0$ ， $\sum Y = 0$ ，可得

$- \frac{{{Q_y}}}{R} + \frac{{{\rm{\partial }} N}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {t^2}}} = 0$

(22)

$\frac{N}{R} + \frac{{{\rm{\partial }} {Q_y}}}{{{\rm{\partial }} x}} - m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} = 0$

(23)

式(22)两端对 $x$ 求一阶导数，可得

$- \frac{{\text{1}}}{R} \cdot \frac{{{\rm{\partial }} Q}}{{{\rm{\partial }} x}} + \frac{{{{\rm{\partial }} ^2}N}}{{{\rm{\partial }} {x^2}}} - m\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} x{\rm{\partial }} {t^2}}} = 0$

(24)

将式(23)代入式(24)，可得

$- \frac{{\text{1}}}{R} \cdot \left( {m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \frac{N}{R}} \right) + \frac{{{{\rm{\partial }} ^2}N}}{{{\rm{\partial }} {x^2}}} - m\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} x{\rm{\partial }} {t^2}}} = 0$

(25)

将式(11)代入式(25)，得

$\begin{split} & - \frac{{\text{1}}}{R} \cdot \left\{ {m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \frac{{\text{1}}}{R}\left[ {EA\left(\frac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} -\frac{v}{R}\right)} \right]} \right\} + \\ &\quad EA\left(\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} {x^3}}} - \frac{1}{R} \cdot \frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}}\right) - m\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} x{\rm{\partial }} {t^2}}} = 0 \end{split}$

(26)

整理得曲梁面内轴向振动微分方程为

$\begin{split} & EA\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} {x^3}}} - m\frac{{{{\rm{\partial }} ^3}u}}{{{\rm{\partial }} x{\rm{\partial }} {t^2}}} - \frac{{EA}}{R} \cdot \frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {x^2}}} - \frac{1}{R}m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} + \\ &\quad\frac{{EA}}{{{R^2}}}\left( {\frac{{{\rm{\partial }} u}}{{{\rm{\partial }} x}} - \frac{v}{R}} \right) = 0 \end{split}$

(27)

式中：多项式 $EA\dfrac{{{\partial ^3}u}}{{\partial {x^3}}} - m\dfrac{{{\partial ^3}u}}{{\partial x\partial {t^2}}}$ 为直梁轴向振动基本情况；多项式 $- \dfrac{{EA}}{R} \cdot \dfrac{{{\partial ^2}v}}{{\partial {x^2}}} - \dfrac{1}{R}m\dfrac{{{\partial ^2}v}}{{\partial {t^2}}} + \dfrac{{EA}}{{{R^2}}}\left( {\dfrac{{\partial u}}{{\partial x}} - \dfrac{v}{R}} \right)$ 为曲梁面内轴弯耦合影响项.

5. 方程退化特例

由于直梁为曲梁特殊情况，Euler梁为Timoshenko梁特殊情况，因此可通过参数调整进行方程退化.

1）当曲梁半径趋向于 $\infty$ 时，曲梁振动微分方程与直梁振动方程一致. 此时将式(21)中曲梁半径R设置为 $\infty$ ，公式为

$\begin{split}& E{I_z}\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^4}}} + m\frac{{{{\rm{\partial }} ^2}v}}{{{\rm{\partial }} {t^2}}} - \rho {I_z}\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^2}{\rm{\partial }} {t^2}}} - \\ &\quad\frac{{E{I_z}k}}{{GA}}m\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {x^2}{\rm{\partial }} {t^2}}} + \frac{{\rho {I_z}k}}{{GA}}m\frac{{{{\rm{\partial }} ^4}v}}{{{\rm{\partial }} {t^4}}} = 0 \end{split}$

(28)

式(21)退化为Timoshenko梁条件下直梁横向弯曲振动微分方程^[7]，即式(28)，从而初步验证了方程的正确性.

同理，将式(27)中半径R设置为 $\infty$ ，公式为

$EA\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {x^2}}} - m\frac{{{{\rm{\partial }} ^2}u}}{{{\rm{\partial }} {t^2}}} = 0$

(29)

式(27)退化为直梁轴向振动微分方程^[7]，即式(29)，从而初步验证了方程的正确性.

2）当曲梁剪切模量G趋向于 $\infty$ ，曲梁转动惯量 $\rho {I_z}$ 设置为0时，方程将不考虑剪切变形与惯性力矩的影响. Timoshenko梁条件下曲梁振动微分方程将与Euler梁条件下曲梁振动方程相一致. 因此将式（21）中剪切模量G设置为 $\infty$ ，曲梁转动惯量 $\rho {I_z}$ 设置为0，方程式为

$\begin{array}{l} \dfrac{{EA}}{R}\dfrac{{{\rm{\partial }}u}}{{{\rm{\partial }}x}} - E{I_z}\left(\dfrac{{{{\rm{\partial }}^4}v}}{{{\rm{\partial }}{x^4}}} + \dfrac{1}{{{R^2}}}\dfrac{{{{\rm{\partial }}^2}v}}{{{\rm{\partial }}{x^2}}}\right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\dfrac{{EA}}{{{R^2}}}v - m\dfrac{{{{\rm{\partial }}^2}v}}{{{\rm{\partial }}{t^2}}} = 0 \end{array}$

(30)

式(21)退化为Euler梁条件下曲梁面内横向弯曲振动微分方程^[5]，即式(30)，从而初步验证了方程的正确性.

6. 结　语

1)参考直梁推导过程，推导建立了曲梁在计入惯性力矩与剪切变形后的面内自由振动微分方程，包括曲梁面内横向弯曲振动微分方程、面内轴向振动微分方程.

2)在直梁的条件下，计入惯性力矩与剪切变形只会对横向弯曲振动造成影响. 而在曲梁的条件下，由于面内轴弯耦合，从而导致惯性力矩与剪切变形对于面内轴向振动也产生间接影响.

3)通过参数调整，经过方程退化初步验证了方程的正确性.

图 1 曲梁平面图

Figure 1. Plan of the curved beam

下载: 全尺寸图片幻灯片

图 2 曲梁微段内力图

Figure 2. Graph of curved beam segment internal force

下载: 全尺寸图片幻灯片

参考文献(8)

[1]	叶康生, 殷振炜. 平面曲梁面内自由振动有限元分析的p型超收敛算法[J] . 工程力学,2019,36(5):28 − 36,52.
[2]	叶康生, 梁童. 平面曲梁面外自由振动有限元分析的p型超收敛算法[J] . 工程力学,2020,37(10):17 − 27. doi: 10.6052/j.issn.1000-4750.2019.11.0694
[3]	陈明飞, 靳国永, 张艳涛, 等. 弹性约束的功能梯度曲梁等几何振动分析[J] . 振动工程学报,2020,33(5):930 − 939.
[4]	李星照, 李朋洲, 孙磊. 曲梁自由振动微分方程的解耦解法及验证[J] . 核动力工程,2016,37(S2):7 − 10.
[5]	宋郁民, 吴定俊, 李奇. 圆弧曲梁振动微分方程推导及振动特性分析[J] . 沈阳建筑大学学报(自然科学版),2012,28(3):400 − 404.
[6]	宋郁民. 曲梁振动微分方程组求解[C]//第23届全国结构工程学术会议论文集(第Ⅰ册). 兰州: 中国力学学会, 中国力学学会《工程力学》编委会, 兰州理工大学, 2014: 258-264.
[7]	包世华. 结构动力学[M]. 武汉: 武汉理工大学, 2017: 105-107.
[8]	李卓庭, 宋郁民. 曲梁几何方程推导[J] . 工程力学,2019,36(S1):12 − 16.

施引文献

期刊类型引用(1)
1. 聂红宾，谷拴成，周志强. 内贴式碳纤维复合材料压阻模型的建立及应用. 合成纤维工业. 2022(04): 68-72 . 百度学术
其他类型引用(2)

资源附件(0)

访问统计

点击查看大图

图(2)

计量

文章访问数: 665
HTML全文浏览量: 391
PDF下载量: 189
被引次数: 3

1. 坐标系及正方向规定
1.1 坐标系规定
1.2 正方向规定
2. 曲梁几何变形协调方程
2.1 不计剪切变形曲梁几何变形协调方程
2.2 计入剪切变形曲梁几何变形协调方程
3. 曲梁内力平衡方程
4. 曲梁面内振动微分方程推导
4.1 面内横向弯曲振动微分方程推导
4.2 面内轴向振动微分方程推导
5. 方程退化特例
6. 结　语

1. 坐标系及正方向规定
1.1 坐标系规定
1.2 正方向规定
2. 曲梁几何变形协调方程
2.1 不计剪切变形曲梁几何变形协调方程
2.2 计入剪切变形曲梁几何变形协调方程
3. 曲梁内力平衡方程
4. 曲梁面内振动微分方程推导
4.1 面内横向弯曲振动微分方程推导
4.2 面内轴向振动微分方程推导
5. 方程退化特例
6. 结　语

参考文献(8)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

考虑惯性力矩与剪切变形的曲梁面内自由振动微分方程的建立

作者简介:
张智超（1997−），男，在读硕士，研究方向为桥梁结构设计与分析. E-mail:1771028705@qq.com

通讯作者:
宋郁民（1976−），男，副教授，博士，研究方向为桥梁结构分析和结构动力学. E-mail:song-yumin@qq.com

计量

Establishment of differential equation of in-plane free vibration of curved beams under MOI and shear deformation

1. 坐标系及正方向规定

1.1 坐标系规定

1.2 正方向规定

2. 曲梁几何变形协调方程

2.1 不计剪切变形曲梁几何变形协调方程

2.2 计入剪切变形曲梁几何变形协调方程

3. 曲梁内力平衡方程

4. 曲梁面内振动微分方程推导

4.1 面内横向弯曲振动微分方程推导

4.2 面内轴向振动微分方程推导

5. 方程退化特例

6. 结　语

期刊类型引用(1)

其他类型引用(2)

计量

目录

1. 坐标系及正方向规定

1.1 坐标系规定

1.2 正方向规定

2. 曲梁几何变形协调方程

2.1 不计剪切变形曲梁几何变形协调方程

2.2 计入剪切变形曲梁几何变形协调方程

3. 曲梁内力平衡方程

4. 曲梁面内振动微分方程推导

4.1 面内横向弯曲振动微分方程推导

4.2 面内轴向振动微分方程推导

5. 方程退化特例

6. 结　语

留言板

考虑惯性力矩与剪切变形的曲梁面内自由振动微分方程的建立

作者简介: 张智超（1997−），男，在读硕士，研究方向为桥梁结构设计与分析. E-mail:1771028705@qq.com

通讯作者: 宋郁民（1976−），男，副教授，博士，研究方向为桥梁结构分析和结构动力学. E-mail:song-yumin@qq.com

计量

出版历程

Establishment of differential equation of in-plane free vibration of curved beams under MOI and shear deformation

1. 坐标系及正方向规定

1.1 坐标系规定

1.2 正方向规定

2. 曲梁几何变形协调方程

2.1 不计剪切变形曲梁几何变形协调方程

2.2 计入剪切变形曲梁几何变形协调方程

3. 曲梁内力平衡方程

4. 曲梁面内振动微分方程推导

4.1 面内横向弯曲振动微分方程推导

4.2 面内轴向振动微分方程推导

5. 方程退化特例

6. 结 语

期刊类型引用(1)

其他类型引用(2)

计量

出版历程

目录

1. 坐标系及正方向规定

1.1 坐标系规定

1.2 正方向规定

2. 曲梁几何变形协调方程

2.1 不计剪切变形曲梁几何变形协调方程

2.2 计入剪切变形曲梁几何变形协调方程

3. 曲梁内力平衡方程

4. 曲梁面内振动微分方程推导

4.1 面内横向弯曲振动微分方程推导

4.2 面内轴向振动微分方程推导

5. 方程退化特例

6. 结 语

作者简介:
张智超（1997−），男，在读硕士，研究方向为桥梁结构设计与分析. E-mail:1771028705@qq.com

通讯作者:
宋郁民（1976−），男，副教授，博士，研究方向为桥梁结构分析和结构动力学. E-mail:song-yumin@qq.com

6. 结　语

6. 结　语