焊缝宽度对对接接头疲劳强度的影响

刘振雄; 徐刚; 曹文涛; 马春伟

焊缝宽度对对接接头疲劳强度的影响

上海工程技术大学材料工程学院，上海 201620

详细信息

作者简介:
刘振雄（1995−），男，在读硕士，研究方向为窄间隙焊接疲劳仿真. E-mail：463456497@qq.com

通讯作者:
马春伟（1970−），男，讲师，博士，研究方向为材料加工和结构完整性. E-mail：macwjx@sues.edu.cn

中图分类号: TG405
计量
- 文章访问数: 627
- HTML全文浏览量: 334
- PDF下载量: 358
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-12
- 刊出日期: 2021-06-30

Influence of weld width on fatigue strength of butt joint

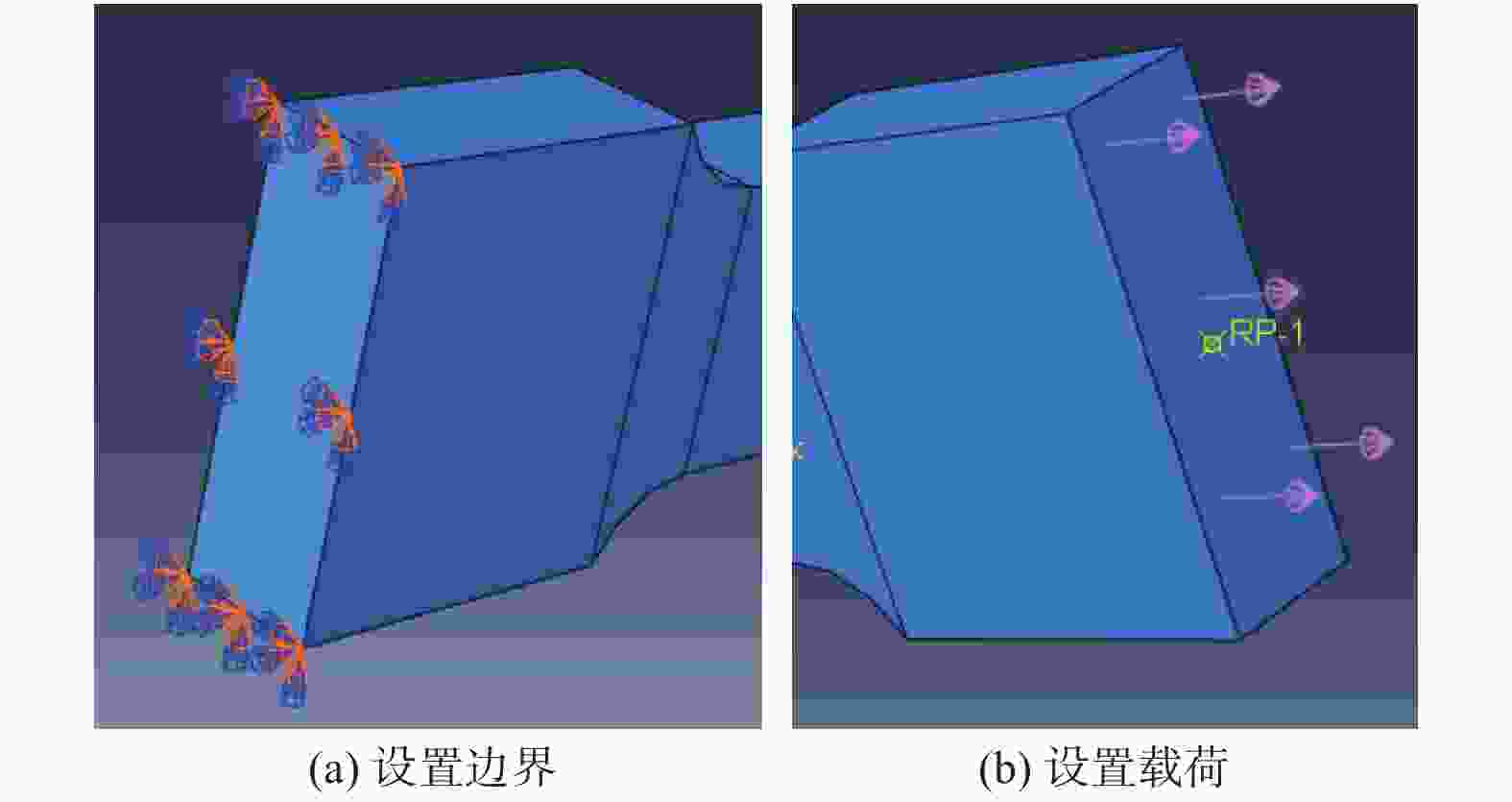
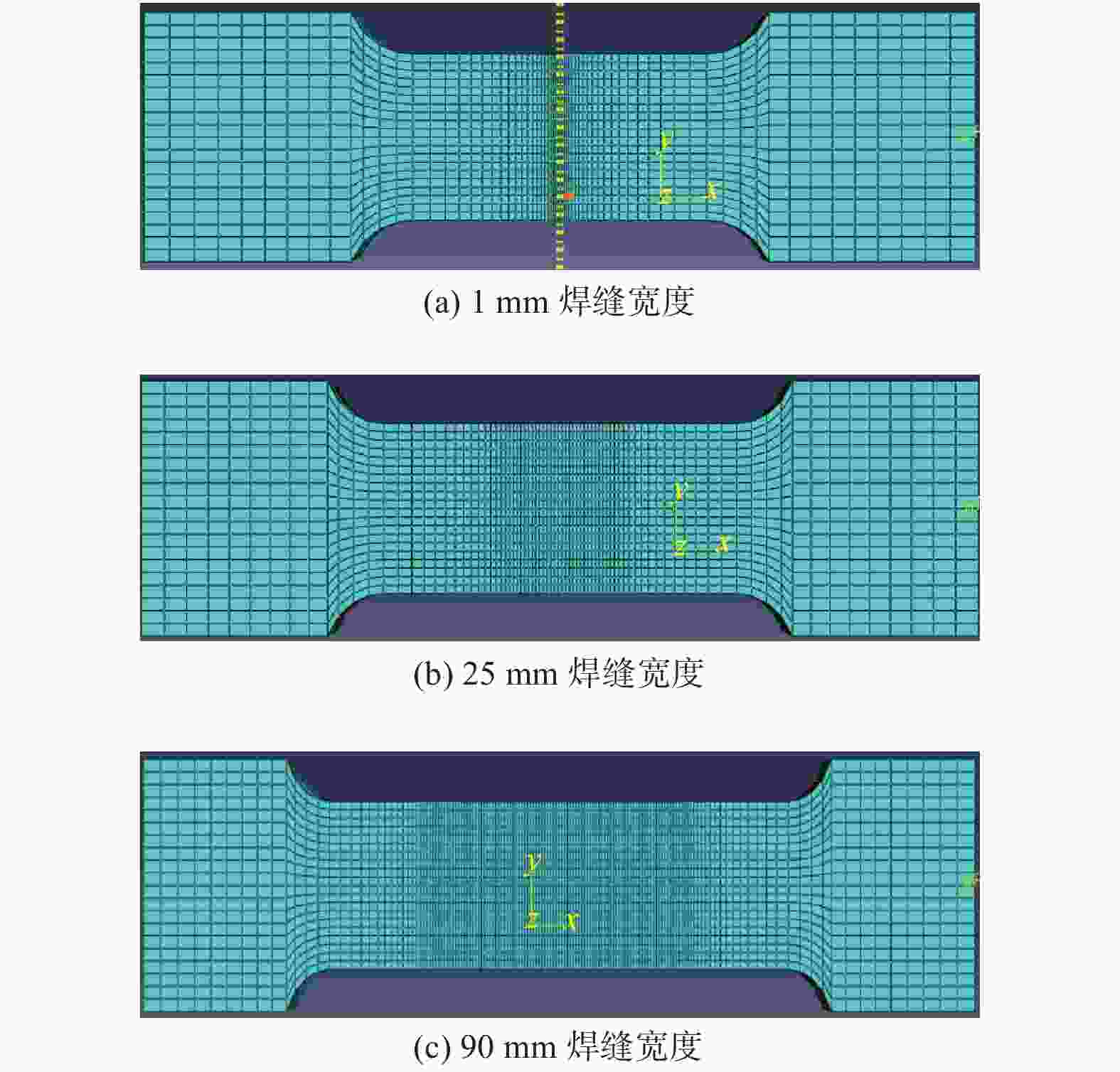
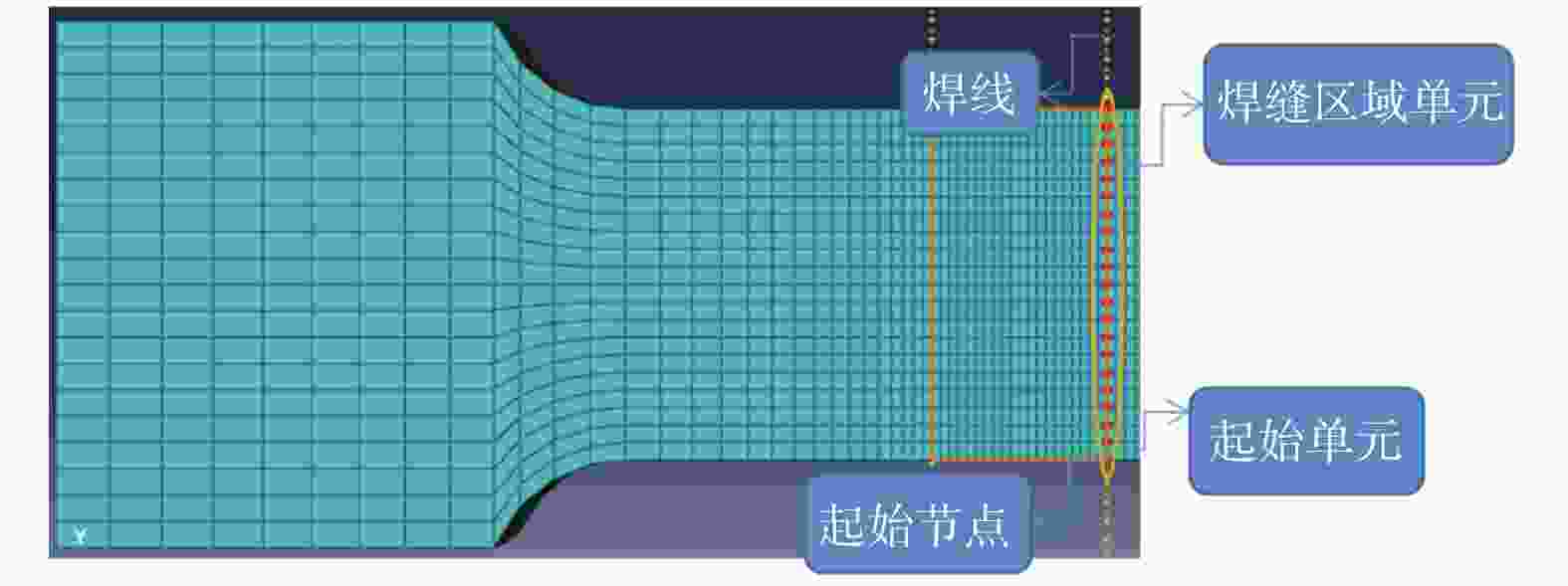
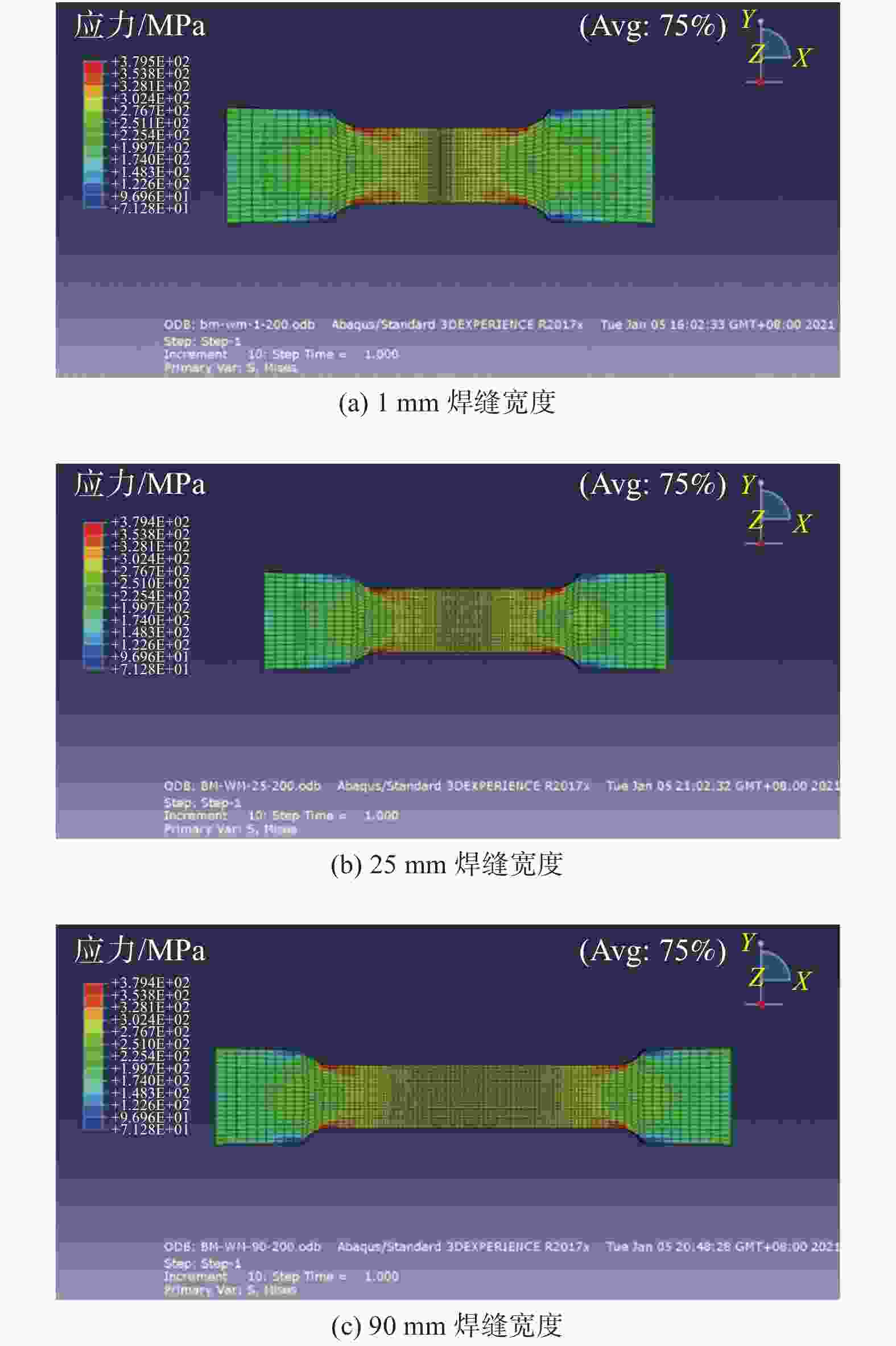
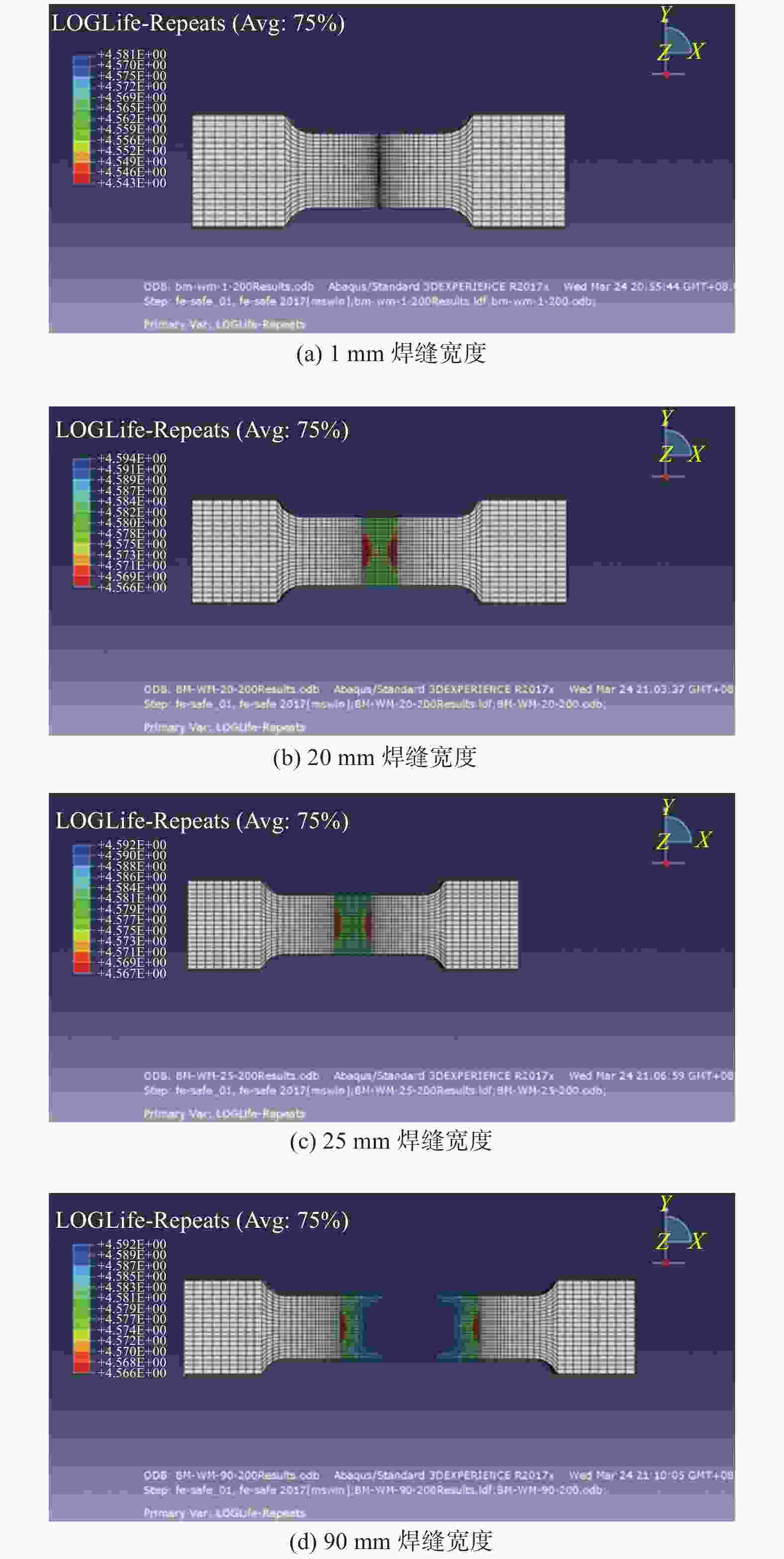
School of Materials Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

摘要: 基于建立的Q235A钢对接接头3D实体模型进行有限元分析，模拟焊缝宽度对焊缝对接接头疲劳强度的影响. 使用ABAQUS CAE软件建立8种不同焊缝宽度几何模型，对模型进行网格划分并计算结构应力. 基于网格不敏感结构应力法分析对接接头的应力，使用ABAQUS软件中Fe-safe模型进行疲劳寿命预测. 模拟结果表明：对接接头焊缝的疲劳性能先随焊缝宽度增大而增强，随着焊缝宽度的继续增大，疲劳性能反而有逐渐减弱的趋势.
- 对接接头 /
- 焊缝宽度 /
- 疲劳寿命 /
- 网格不敏感结构应力法
Abstract: Finite element analysis based on the establishment of a 3D solid model of the butt joint of Q235A steel was conducted, and the influence of weld width on the fatigue strength of the butt joint was simulated. Eight geometric models of different weld widths were established by ABAQUS CAE software. The meshing of the model was carried out and the structural stress was calculated. The stress of butt joint was analyzed based on mesh insensitive structural stress method. The Fe-safe model of ABAQUS software was used to predict the fatigue life. The simulation results show that the fatigue properties of butt joint weld firstly increase with the increase of weld width, and then gradually decrease with the increase of weld width.
- butt joint /
- weld width /
- fatigue life /
- mesh insensitive structural stress method

HTML全文

图 1 名义应力示意图

Figure 1. Nominal stress diagram

下载: 全尺寸图片幻灯片

图 2 基于厚度的结构应力

Figure 2. Structural stress based on thickness

下载: 全尺寸图片幻灯片

图 3 焊趾处沿板厚方向的非线性应力分布

Figure 3. Nonlinear stress distribution at weld toe along plate thickness direction

下载: 全尺寸图片幻灯片

图 4 对接接头三维几何模型

Figure 4. Three-dimensional geometric model of butt joints

下载: 全尺寸图片幻灯片

图 5 对接接头载荷及约束定义

Figure 5. Definition of load and constraint for butt joints

下载: 全尺寸图片幻灯片

图 6 对接接头的有限元网格

Figure 6. Finite element mesh of butt joint

下载: 全尺寸图片幻灯片

图 7 有限元模型定义的相关参量

Figure 7. Related parameters defined by finite element model

下载: 全尺寸图片幻灯片

图 8 对接接头Mises应力云图

Figure 8. Mises stress nephogram of butt joint

下载: 全尺寸图片幻灯片

图 9 对接接头疲劳寿命云图

Figure 9. Fatigue life nephogram of butt joint

下载: 全尺寸图片幻灯片

表 1 材料力学性能

Table 1. Mechanical properties of materials

材料	屈服强度/MPa	抗拉强度/MPa	弹性模量/MPa	泊松比
Q235A	225	450	200000	0.3
JM56	430 ( ≥400 )	480	210000	0.3

下载: 导出CSV

表 2 材料化学组成成分

Table 2. Chemical constituents of materials %

材料	C	Mn	Si	S	P
Q235A	≤0.220	≤1.400	≤0.350	≤0.050	≤0.045
JM56	0.060~0.150	1.400~1.850	0.800~1.150	≤0.025	≤0.035

下载: 导出CSV

表 3 对接接头应力集中系数

Table 3. Stress concentration factors of butt joints

应力集中系数	焊缝宽度/mm
应力集中系数	1	10	20	25	30	50	70	90
SCF	1.535	1.521	1.517	1.516	1.517	1.525	1.526	1.529

下载: 导出CSV

表 4 疲劳强度与性能

Table 4. Fatigue strength and performance

焊缝宽度/mm	应力/MPa	疲劳寿命/次	损伤比	累积损伤比
1	200	4.226E+06	0.156	0.384
	210	3.486E+06	0.096
	220	3.149E+06	0.132
10	200	4.380E+06	0.150	0.371
	210	3.621E+06	0.091
	220	3.235E+06	0.130
20	200	4.558E+06	0.145	0.359
	210	3.691E+06	0.085
	220	3.352E+06	0.129
25	200	4.571E+06	0.143	0.348
	210	3.721E+06	0.081
	220	3.345E+06	0.124
30	200	4.550E+06	0.145	0.359
	210	3.658E+06	0.086
	220	3.262E+06	0.128
50	200	4.465E+06	0.148	0.368
	210	3.436E+06	0.090
	220	3.165E+06	0.130
70	200	4.454E+06	0.148	0.371
	210	3.398E+06	0.091
	220	3.109E+06	0.132
90	200	4.332E+06	0.151	0.378
	210	3.298E+06	0.092
	220	3.168E+06	0.135

下载: 导出CSV

参考文献(13)

[1]	陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002: 1 − 90.
[2]	方洪渊. 焊接结构学[M]. 北京: 机械工业出版社, 2008: 78 − 112.
[3]	BONI L, LANCIOTTI A, POLESE C. “Size effect” in the fatigue behavior of Friction Stir Welded plates[J] . International Journal of Fatigue,2015,80(3):238 − 245.
[4]	JAURRIETA M A, ALONSO A, CHICA J A, et al. Tubular Structures X[C]//Proceedings of the 10th International Symposium on Tubular Structures. Abingdon: TaylorFrancis, 2017: 365 – 374.
[5]	张欣, 高世一, 吴文兵, 等. 焊缝余高对焊接接头疲劳寿命影响的有限元分析[J] . 热加工工艺,2017,46(1):189 − 194.
[6]	冯继军. 焊接结构件的疲劳分析[J] . 焊接技术,2017,46(6):78 − 80.
[7]	DONG P S, HONG J K,JESUS A M. Analysis of recent fatigue data using the structural stress procedure in ASME Div 2 rewrite[J] . Journal of Pressure Vessel Technology,2007,19(3):355 − 362.
[8]	DONG P. A structural stress definition and numerical implementation for fatigue analysis of welded joints[J] . International Journal of Fatigue,2001,23(10):865 − 876. doi: 10.1016/S0142-1123(01)00055-X
[9]	ZERBST U, HENSEL J. Application of fracture mechanics to weld fatigue[J] . International Journal of Fatigue,2020,2(3):139 − 141.
[10]	李林平, 梁军, 赵雷, 等. 高、低匹配对G115/T92异种钢接头组织与力学性能的影响[J] . 机械工程材料,2018,42(10):51 − 57. doi: 10.11973/jxgccl201810010
[11]	吴松林, 薛钢, 曲占元. 低匹配对接接头尺寸设计原则研究[J] . 材料开发与应用,2014,29(1):14 − 17.
[12]	赵峰. 基于网格不敏感结构应力的铝合金焊接接头疲劳性能分析[D]. 大连: 大连交通大学, 2013.
[13]	罗超, 张锦华, 王琰, 等. 板厚对不锈钢车体激光叠焊接头抗剪强度和疲劳强度的影响[J] . 焊接,2021(2):57 − 61.