Hybrid Fundamental-Solution-Based FEM for Heat Conduction Problems in Orthotropic Materials
-
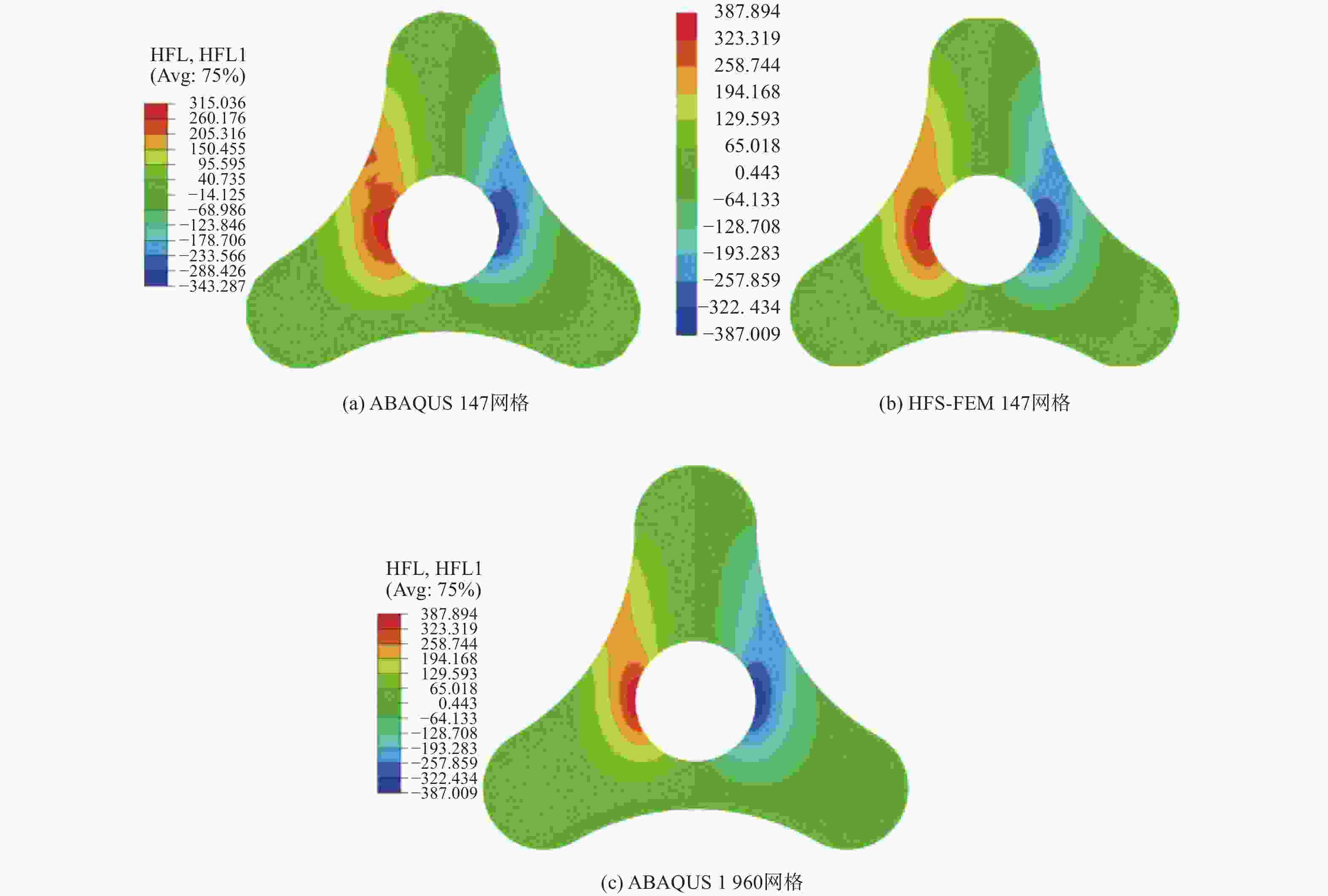
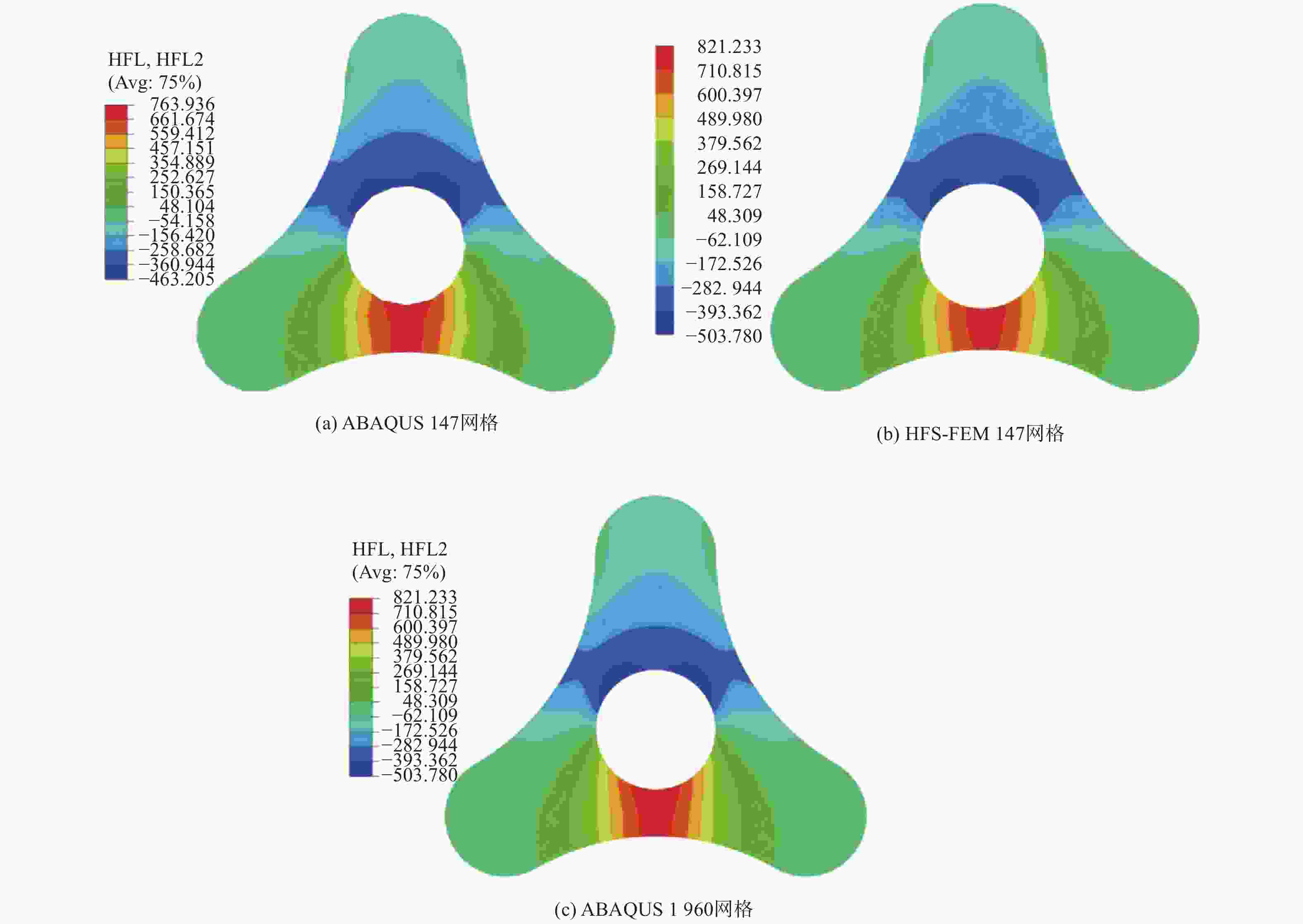
摘要: 采用基于杂交基本解的有限元法（HFS-FEM）对二维正交各向异性材料进行热传导分析. 单元域内和单元边界上的温度分布由两个温度场独立描述. 采用基本解的线性组合来近似单元内部温度场，采用标准一维线单元形函数来定义网线温度场. 利用修正变分泛函和散度定理导得相应的有限元列式，通过2个算例与ABAQUS结果对比，验证了该方法具有有效性. 数值结果表明，该方法在单元形状极度扭曲情形下仍能保持良好的精度，这是区别于传统有限元法的显著特点.Abstract: A heat conduction analysis of two-dimensional orthotropic materials was carried out by the hybrid fundamental-solution-based finite element method (HFS-FEM). Temperature distributions within the element domain and on the element boundary were independently described by two temperature fields. A linear combination of fundamental solutions was utilized to approximate the intra-element temperature field while standard one-dimensional shape functions were employed to define the frame temperature field. By virtue of the modified variational functional and divergence theorem, the resultant finite element formulation was derived. The effectiveness of the proposed method was verified by comparing two numerical examples with ABAQUS result. The numerical results demonstrate that the proposed method can still keep excellent accuracy even when the element shape degenerates to a situation of extreme distortion. This is one of marked features which differs from conventional finite element methods.
-
图 3 正方形区域、边界条件和有限元网格
Figure 3. Square domain, boundary conditions and finite element mesh
图 5 温度u和热流分量
${{{q}}_{{x}}}$ 的相对误差Figure 5. Relative errors of temperature
${{u}}$ and heat flux component${{{q}}_{{x}}}$ 
图 7 三角陀螺域，边界条件及有限元网格
Figure 7. Trigonometric gyroscopic domain, boundary conditions and finite element mesh
图 8 三角陀螺域温度云图
Figure 8. Cloud maps of temperature in the trigonometric gyroscopic domain
图 9 三角陀螺域热流分量qx云图
Figure 9. Cloud maps of heat flux component
${{{q}}_x}$ in the trigonometric gyroscopic domain
图 10 三角陀螺域热流分量qy云图
Figure 10. Cloud maps of heat flux component
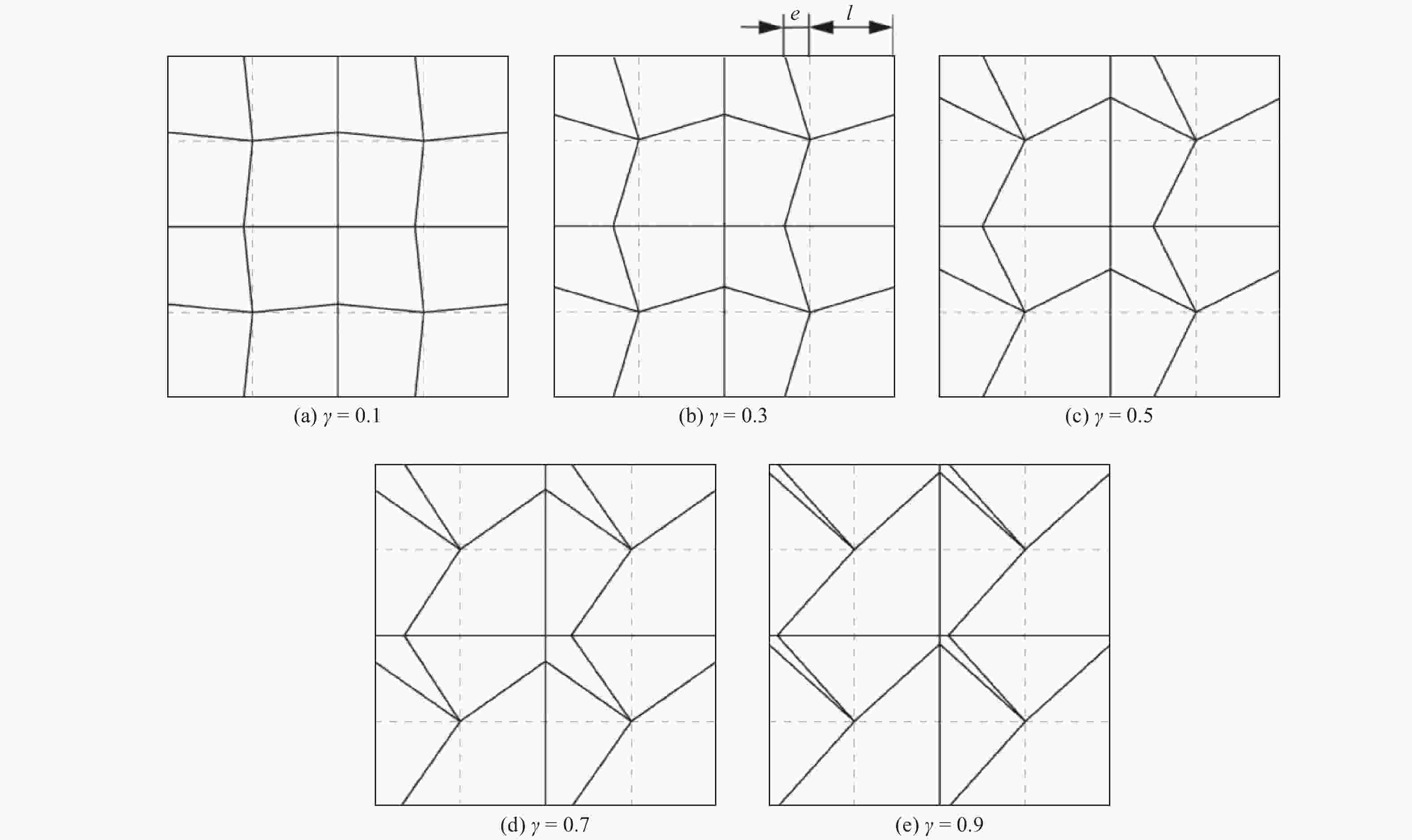
${{{q}}_y}$ in trigonometric gyroscopic domain表 1 不同网格畸变下选定5个点的温度结果
Table 1. Results of temperatures at selected five points under different mesh distortions
坐标 $\gamma $=0 $\gamma $=0.1 $\gamma $=0.3 $\gamma $=0.5 $\gamma $=0.7 $\gamma $=0.9 (0.05,0.025) 5.0778 5.0771 5.0788 5.0809 5.0801 5.0596 (0.025,0.025) 2.5386 2.5478 2.5508 2.5525 2.5523 2.5487 (0.035,0.075) 3.6361 3.6393 3.6332 3.6439 3.6471 3.6268 (0.075,0.075) 7.6275 7.6205 7.6280 7.6216 7.6275 7.6356 (0.015,0.045) 1.5415 1.5408 1.5401 1.5430 1.5472 1.5509 
下载: 导出CSV
-
[1] WANG H, QIN Q H. Hybrid FEM with fundamental solutions as trial functions for heat conduction simulation[J] . Acta Mechanica Solida Sinica,2009,22(5):487 − 498. [2] GAO X W. A meshless BEM for isotropic heat conduction problems with heat generation and spatially varying conductivity[J] . International Journal for Numerical Methods in Engineering,2006,66(9):1411 − 1431. [3] KASSAB A J, DIVO E. A generalized boundary integral equation for isotropic heat conduction with spatially varying thermal conductivity[J] . Engineering Analysis with Boundary Elements,1996,18(4):273 − 286. [4] WANG Z, YAN P, GUO Z, et al. BEM/FDM conjugate heat transfer analysis of a two-dimensional air-cooled turbine blade boundary layer[J] . Journal of Thermal Science,2008,17(3):199 − 206. [5] DUDA P, Institute of Thermal Power Engineering, Faculty of Mechanical Engineering, et al. Finite element method formulation in polar coordinates for transient heat conduction problems[J] . Journal of Thermal Science,2016,25(2):188 − 194. [6] MERA N S, ELLIOTT L, INGHAM D B, et al. A comparison of boundary element method formulations for steady state anisotropic heat conduction problems[J] . Engineering Analysis with Boundary Elements,2001,25(2):115 − 128. [7] PEREZ M M, WROBEL L C. Use of isotropic fundamental solutions for heat conduction in anisotropic media[J] . International Journal of Numerical Methods for Heat and Fluid Flow,1993,3(1):49 − 62. [8] GAO X W. Source point isolation boundary element method for solving general anisotropic potential and elastic problems with varying material properties[J] . Engineering Analysis with Boundary Elements,2010,34(12):1049 − 1057. [9] WANG H M, QIN Q H, KANG Y L. A new meshless method for steady-state heat conduction problems in anisotropic and inhomogeneous media[J] . Archive of Applied Mechanics,2005,74(8):563 − 579. [10] PEREZ M M, WROBEL L C. A general integral equation formulation for homogeneous orthotropic potential problems[J] . Engineering Analysis with Boundary Elements,1992,10(4):323 − 332. [11] DIVO E, KASSAB A J. A generalized boundary-element method for steady-state heat conduction in heterogeneous anisotropic media[J] . Numerical Heat Transfer, Part B: Fundamentals,1997,32(1):37 − 61. [12] ZHOU H L, TIAN Y, YU B, et al. The natural boundary integral equation of the orthotropic potential problem[J] . Engineering Analysis with Boundary Element,2016,62:186 − 192. [13] JIROUSEK J, LEON N. A powerful finite element for plate bending[J] . Computer Methods in Applied Mechanics and Engineering,1977,12(1):77 − 96. [14] WANG K Y, ZHANG L Q, LI P C. A four-node hybrid-Trefftz annular element for analysis of axisymmetric potential problems[J] . Finite Elements in Analysis and Design,2012,60:49 − 56. [15] 王克用, 岑皓, 李培超. 位势问题Trefftz有限元法的研究进展[J] . 上海工程技术大学学报,2017,31(3):204 − 209. doi: 10.3969/j.issn.1009-444X.2017.03.003 [16] WANG K Y. A four-node hybrid-Trefftz plane elasticity element with fundamental analytical solutions[J] . Advanced Materials Research,2011,279:194 − 199. [17] SHE Z, WANG K Y, LI P C. Hybrid Trefftz polygonal elements for heat conduction problems with inclusions/voids[J] . Computers & Mathematics with Applications,2019,78(6):1978 − 1992. [18] SHE Z, WANG K Y, LIU H. Thermal analysis of elliptical fiber-reinforced composites by the hybrid Trefftz finite element method[J] . International Journal of Heat and Mass Transfer,2019,144:118596. [19] WANG K Y, QIN Q H, KANG Y L, et al. A direct constraint-Trefftz FEM for analysing elastic contact problems[J] . International Journal for Numerical Methods in Engineering,2005,63(12):1694 − 1718. [20] ZHOU J C, WANG K Y, LI P C, et al. Hybrid fundamental solution based finite element method for axisymmetric potential problems[J] . Engineering Analysis with Boundary Elements,2018,91:82 − 91. [21] 高可乐, 王克用. 轴对称热弹性问题杂交基本解Trefftz有限元分析[J] . 上海工程技术大学学报,2020,34(1):54 − 58, 75. doi: 10.3969/j.issn.1009-444X.2020.01.010 [22] WANG K Y, HUANG Z M, LI P C, et al. Trefftz finite element analysis of axisymmetric potential problems in orthotropic media[J] . Applied Mathematics and Mechanics,2013,34(5):462 − 469. [23] WANG K Y, LI P C, WANG D Z. Trefftz-type FEM for solving orthotropic potential problems[J] . Latin American Journal of Solids and Structures,2014,11(14):2537 − 2554. [24] 王克用, 李培超. 变系数位势问题的Trefftz有限元法[J] . 上海工程技术大学学报,2014,28(1):58 − 62, 67. doi: 10.3969/j.issn.1009-444X.2014.01.013 [25] 刘博, 王克用, 王明红. 轴对称Poisson方程的Trefftz有限元解法[J] . 应用数学和力学,2015,36(2):140 − 148. doi: 10.3879/j.issn.1000-0887.2015.02.003 [26] KOMPIŠ V, BÚRY J. Hybrid-Trefffz finite element formulations based on the fundamental solution[C] // Proceedings of IUTAM Symposium on Discretization Methods in Structural Mechanics, Solid Mechanics and its Applications. Dordrecht: Springer, 1999: 181-187. [27] 高可乐, 王克用, 李培超. 考虑体力的轴对称弹性问题杂交基本解有限元法[J] . 轻工机械,2020,38(1):5 − 11, 17. [28] CAO L L, WANG H, QIN Q H. Fundamental solution based graded element model for steady-state heat transfer in FGM[J] . Acta Mechanica Solida Sinica,2012,25(4):377 − 392. -
下载:
点击查看大图
计量
- 文章访问数: 448
- HTML全文浏览量: 418
- PDF下载量: 224
- 被引次数: 0
