基于广义双参数最弱链统计模型分析纤维断裂强度与尺寸的相关性

竺宇洋; 翟建广; 高春; 卢惠亲

基于广义双参数最弱链统计模型分析纤维断裂强度与尺寸的相关性

上海工程技术大学材料工程学院，上海 201620

详细信息

作者简介:
竺宇洋（1995−），男，在读硕士，研究方向为纤维复合材料力学性能. E-mail：752479748@qq.com

通讯作者:
翟建广（1976−），男，讲师，博士，研究方向为功能性复合材料. E-mail：zhai_jianguang@sues.edu.cn

中图分类号: TB 332
计量
- 文章访问数: 118
- HTML全文浏览量: 108
- PDF下载量: 127
- 被引次数: 0
出版历程
- 收稿日期: 2020-09-25
- 刊出日期: 2021-03-30

Analysis of Correlation Between Fiber Breaking Strength and Size Based on Generalized Two-Parameter Weakest Chain Statistical Model

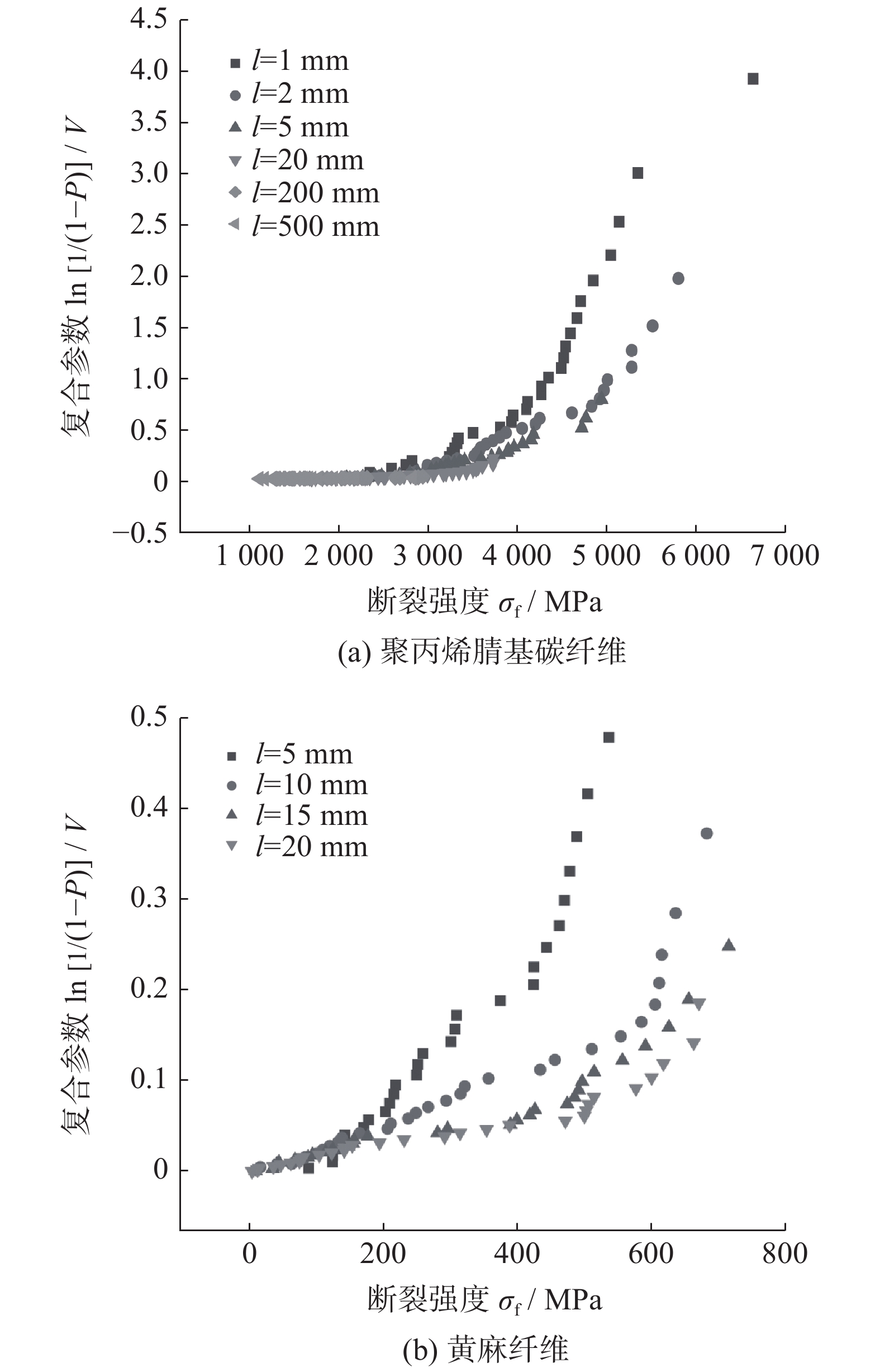
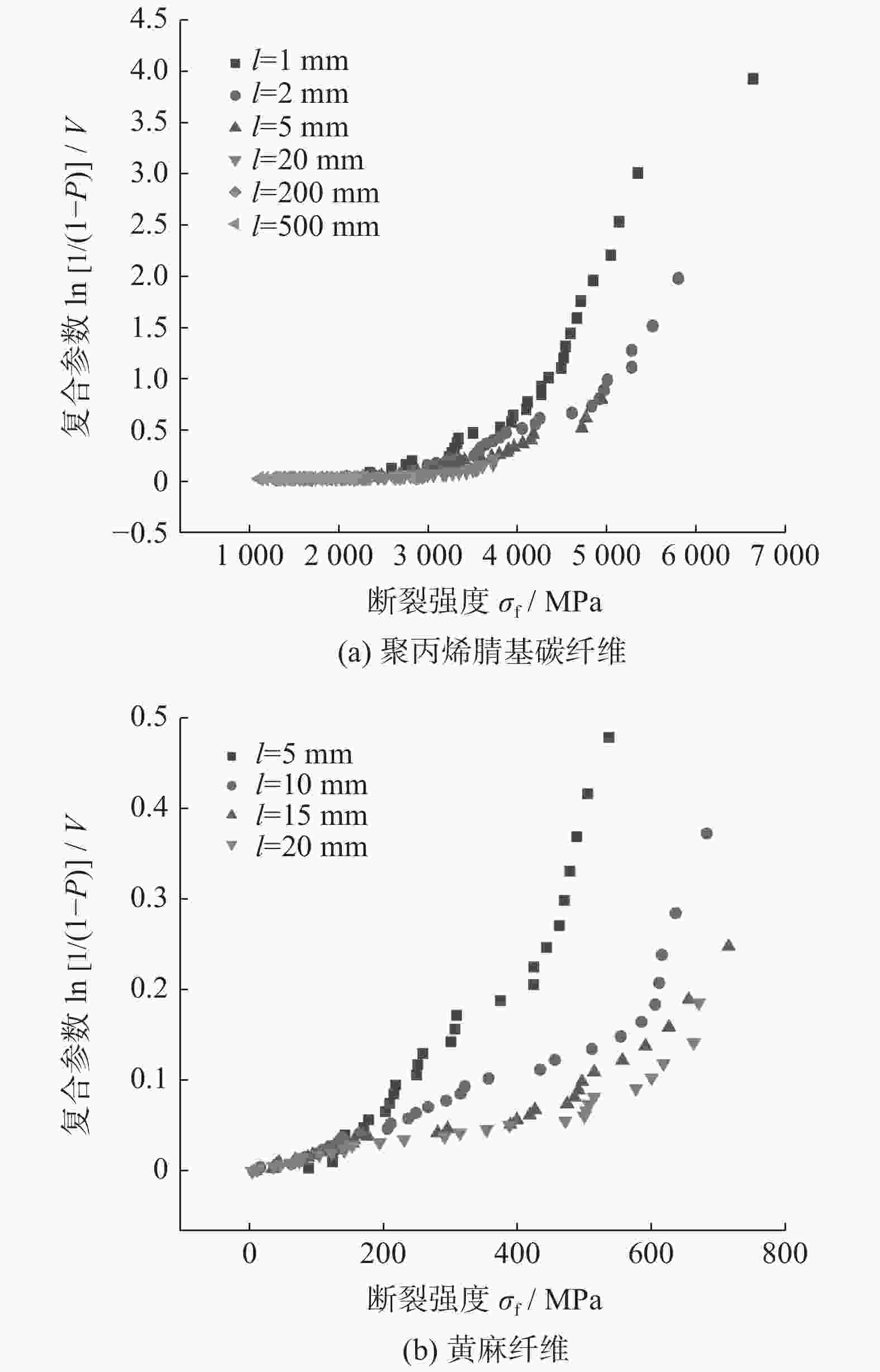
School of Materials Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

摘要: 为探究纤维断裂强度与尺寸之间的相关性，通过一种改进的广义双参数最弱链统计模型分别对不同标距尺寸下聚丙烯腈基碳纤维和黄麻纤维的断裂强度数据进行统一处理. 通过引入指数参量β，表征缺陷实际空间分布与理想均匀空间分布条件的偏离程度，将纤维断裂强度和尺寸作为统计参量，得到的纤维失效函数综合反映纤维断裂强度和尺寸对失效概率的影响，较好地描述了纤维断裂强度和尺寸之间的相关性.
- 尺寸效应 /
- 纤维 /
- 空间缺陷分布 /
- 统计模型
Abstract: In order to explore the correlation between fiber breaking strength and size, an improved generalized two-parameter weakest chain statistical model was used to uniformly process the breaking strength data of polyacrylonitrile-based (PAN-based) carbon fiber and jute fiber under different gauge lengths. An exponential parameter β was introduced to characterize the degree of deviation between the actual spatial distribution of defects and the ideal uniform spatial distribution conditions. By taking fiber breaking strength and size as statistical parameters, the obtained fiber failure function can collectively reflect the influence of fiber breaking strength and size on the probability of fiber failure, and better describe the correlation between fiber breaking strength and size.
- size effect /
- fiber /
- spatial defect distribution /
- statistical model

HTML全文

图 1 不同标距长度下双参数Weibull统计分布函数

Figure 1. Two-parameter Weibull statistical distribution function under different gauge lengths

下载: 全尺寸图片幻灯片

图 2 不同标距长度下广义双参数最弱链统计分布函数

Figure 2. Generalized two-parameter weakest chain statistical distribution function under different gauge lengths

下载: 全尺寸图片幻灯片

表 1 不同标距长度下的Weibull参数

Table 1. Weibull parameters under different gauge lengths

纤维类型	标距长度l / mm	Weibull模量m	特征强度$ {\sigma }_{0} $ / MPa
聚丙烯腈基碳纤维	1	5.65	4749
	2	6.06	4577
	5	6.67	4131
	20	7.86	3576
	200	6.29	2557
	500	6.95	2206
黄麻纤维	5	2.18	436
	10	1.41	415
	15	1.27	410
	20	1.19	377

下载: 导出CSV

参考文献(16)

[1]	WILSON D M. Statistical tensile strength of Nextel^TM 610 and Nextel^TM 720 fibres[J] . Journal of Materials Science,1997,32(10):2535 − 2542. doi: 10.1023/A:1018538030985
[2]	吴琪琳, 潘鼎. 国产黏胶基碳纤维强度的两种统计分布[J] . 材料导报,2000,14(11):55 − 56. doi: 10.3321/j.issn:1005-023X.2000.11.021
[3]	李敏洁, 汪泽幸, 陈南梁. Vectran长丝断裂强力的Weibull分布统计分析[J] . 丝绸,2012, 49(10):11 − 15.
[4]	WANG F, SHAO J X, KEER L M, et al. The effect of elementary fibre variability on bamboo fibre strength[J] . Materials & Design,2015,75:136 − 142.
[5]	PICKERING K L, MURRAY T L. Weak link scaling analysis of high-strength carbon fibre[J] . Composites Part A: Applied Science and Manufacturing,1999,30(8):1017 − 1021. doi: 10.1016/S1359-835X(99)00003-2
[6]	XIA Z P, YU J Y, CHENG L D, et al. Study on the breaking strength of jute fibres using modified Weibull distribution[J] . Composites Part A: Applied Science and Manufacturing,2009,40(1):54 − 59. doi: 10.1016/j.compositesa.2008.10.001
[7]	马春杰, 宁荣昌, 李琳, 等. 用Weibull方法评价化学介质对PBO纤维统计强度的影响[J] . 复合材料学报,2005,22(3):16 − 20. doi: 10.3321/j.issn:1000-3851.2005.03.003
[8]	车辙, 李敏, 李庆辉, 等. PBO和芳纶纤维单丝拉伸性能影响因素分析[J] . 宇航材料工艺,2018,48(6):89 − 93.
[9]	WATSON A S, SMITH R L. An examination of statistical theories for fibrous materials in the light of experimental data[J] . Journal of Materials Science,1985,20(9):3260 − 3270. doi: 10.1007/BF00545193
[10]	YAO J W, YU W D, PAN D. Tensile strength and its variation of PAN-based carbon fibers. III. weak-link analysis[J] . Journal of Applied Polymer Science,2008,110(6):3778 − 3784. doi: 10.1002/app.24879
[11]	WATANABE J, TANAKA F, OKUDA H, et al. Tensile strength distribution of carbon fibers at short gauge lengths[J] . Advanced Composite Materials,2014,23(5/6):535 − 550. doi: 10.1080/09243046.2014.915120
[12]	GRIFFITH A A. The phenomena of rupture and flows in solids[J] . Philosophical Transactions of the Royal Society of London: Series A,1921,221:163 − 198.
[13]	BATDORF S B, Jr HEINISCH H L. Weakest link theory reformulated for arbitrary fracture criterion[J] . Journal of the American Ceramic Society,2010,61(7/8):355 − 358.
[14]	LEI W S. Evaluation of the basic formulations for the cumulative probability of brittle fracture with two different spatial distributions of microcracks[J] . Fatigue & Fracture of Engineering Materials & Structures,2016,39(5):611 − 623.
[15]	LEI W S. A generalized weakest-link model for size effect on strength of quasi-brittle materials[J] . Journal of Materials Science,2018,53(2):1227 − 1245. doi: 10.1007/s10853-017-1574-8
[16]	BENJEDDOU O. Weibull statistical analysis and experimental investigation of size effects on tensile behavior of dry unidirectional carbon fiber sheets[J] . Polymer Testing,2020,86:106498. doi: 10.1016/j.polymertesting.2020.106498