Research on Dynamic Simulation of Eight Degrees of Freedom Automobile Model
-
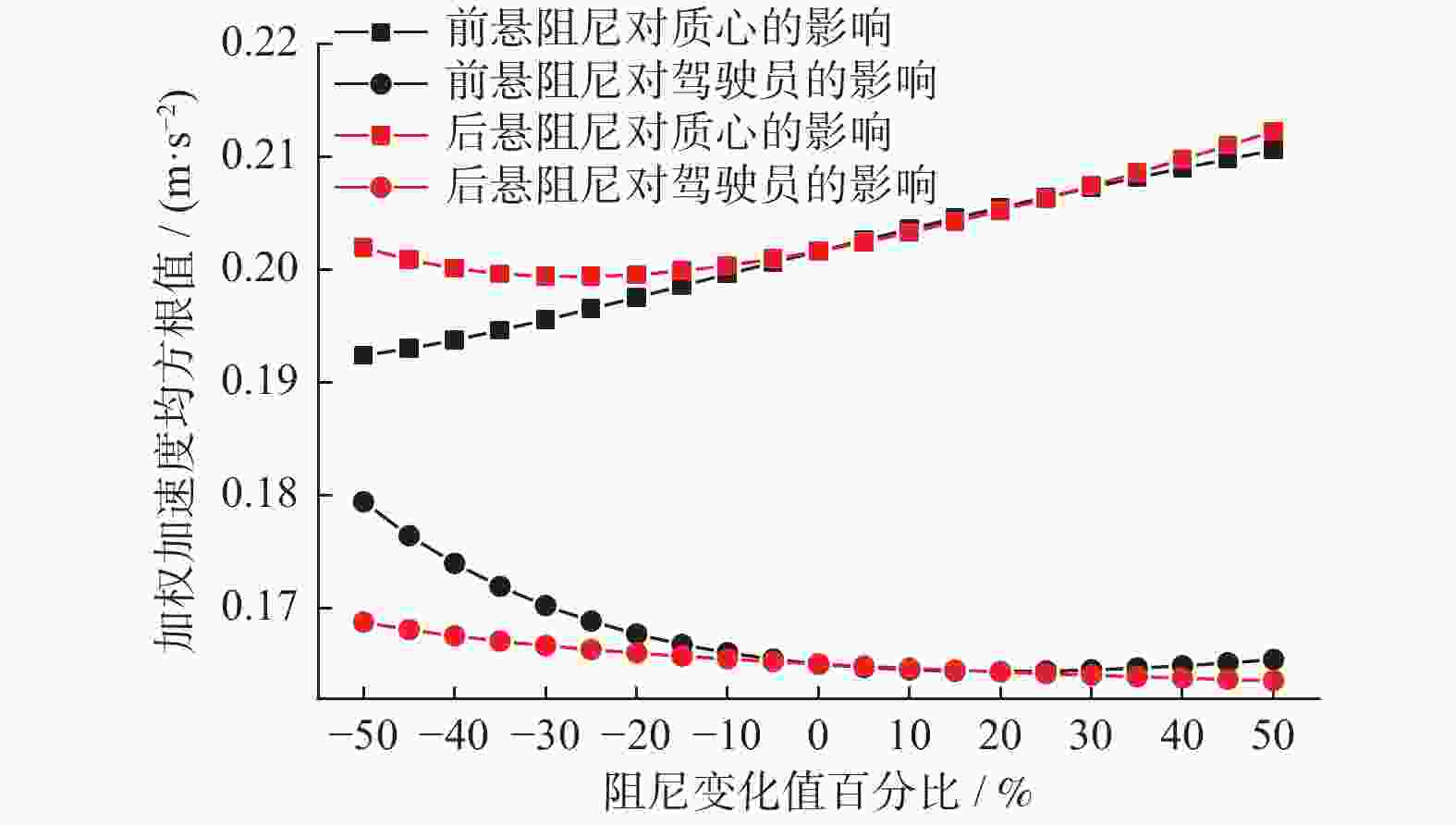
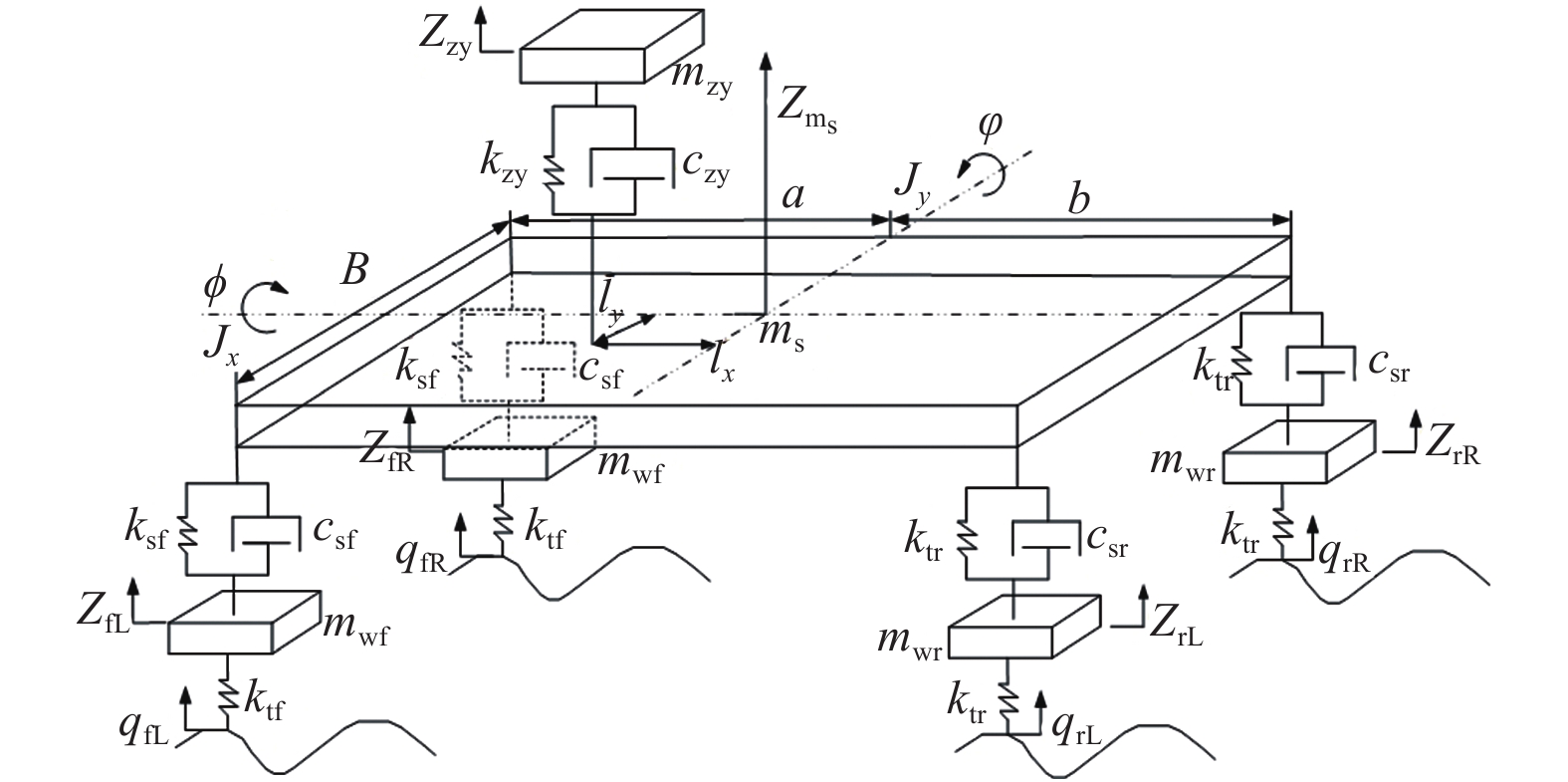
摘要: 汽车振动系统是一个非常复杂的系统. 为达到准确反映整车振动情况，基于一定假设，在Matlab软件中利用牛顿法建立某汽车八自由度振动模型. 分析整车动态时域响应特性，基于滤波白噪声和二阶Pade算法，建立四轮相关路面模型. 验证路面精确度，并将其作为激励输入整车振动模型，利用Newmark显式积分法进行求解，将各响应量时域信号转化为频域响应信号并与该振动系统的频域仿真对比. 结果证明该模型的可靠性好，求解速度快. 进一步研究车身质心位置、悬架刚度、轮胎刚度和悬架阻尼等因素对驾驶员与车身质心处舒适性的影响，并基于原车参数提出改善整车舒适性的建议.
-
关键词:
- 平顺性 /
- 整车 /
- 二阶Pade算法 /
- Newmark显式积分
Abstract: The vehicle vibration system is a very complex system. In order to accurately reflect the vibration of the whole vehicle, based on certain assumptions, the eight degrees of freedom vibration model for a car was established by using Newton method in Matlab software. Based on the analysis of vehicle dynamic response characteristics in time domain, a four-wheel correlation road model was established based on filtered white noise and the second-order Pade algorithm. The accuracy of the road surface was verified, and it was used as the excitation input to the vehicle vibration model. The Newmark explicit integration method was used to solve the problem. The time-domain signal of each response was transformed into the frequency-domain response signal, and compared with the frequency-domain simulation of the vibration system. The results show that the model has good reliability and fast solution speed. Furthermore, the influences of the position of body mass center, suspension stiffness, tire stiffness and suspension damping on the comfort of driver and body centroid were further studied. Based on the original vehicle parameters, suggestions for improving vehicle comfort were put forward.-
Key words:
- riding comfort /
- vehicle /
- second-order Pade algorithm /
- Newmark explicit integration
-
图 2 四轮汽车B级路面不平度模拟曲线
Figure 2. Simulation curve of B class road roughness for four-wheel automobile
表 1 某轿车的主要性能参数
Table 1. Main performance parameters of a car
参数 数值 车身质量${m_{\rm{s}}}/{\rm{kg}}$ 1 000 车身俯仰转动惯量$ {J_{{y}}}/ ({\rm{kg \cdot {m^2}}}) $ 803 车身侧倾转动惯量$ {J_{{x}}}/({\rm{kg \cdot {m^2}}}) $ 429 前轮簧下质量${m_{{\rm{wf}}} }/{\rm{kg}}$ 59 后轮簧下质量${m_{{\rm{wr}}} }/{\rm{kg}}$ 53 驾驶员及座椅质量${m_{{\rm{zy}}} }/{\rm{kg}}$ 60 前、后轮胎刚度$ {k}_{{\rm{tf}}}$、${k}_{{\rm{tr}}}/({\rm{N \cdot m^{-1}}})$ 96 000 前悬架刚度${k_{{\rm{sf}}} }/({\rm{N \cdot m^{-1}}})$ 16 500 后悬架刚度${k_{{\rm{sr}}} }/({\rm{N \cdot m^{-1}}})$ 14 500 驾驶员座椅刚度${k_{{\rm{zy}}} }/({\rm{N \cdot m^{-1}}})$ 8 000 前、后悬架阻尼$ {c}_{{\rm{sf}}}$、${c}_{{\rm{sr}}}/({\rm{N\cdot s \cdot m^{-1}}})$ 1 140 驾驶员座椅阻尼${c_{{\rm{zy}}} }/({\rm{N \cdot s\cdot m^{-1}}})$ 350 前轴到车身质心距离$a/{\rm m}$ 0.894 后轴到车身质心距离$b/{\rm m}$ 1.446 前、后轮距$ B/{\rm m} $ 1.4 驾驶员座椅中心到横轴的距离${l_{{x}}}/{\rm m}$ 0.331 驾驶员座椅中心到纵轴的距离${l_{{y}}}/{\rm m}$ 0.35 
下载: 导出CSV
表 2
${a_w}$ 与人主观感觉的关系Table 2. Relationship of
${a_w}$ and people′s subjective feeling${a_w}$ 人主观感受 <0.315 没有不舒适 0.315～0.63 有些不舒适 0.5～1.0 相当不舒适 0.8～1.6 不舒适 1.25～2.5 很不舒适 >2.0 极不舒适
下载: 导出CSV
-
[1] 喻凡, 林逸. 汽车系统动力学[M]. 2版. 北京: 机械工业出版社, 2017. [2] 张立军, 何辉. 车辆行驶动力学理论及应用[M]. 北京: 国防工业出版社, 2011. [3] 吴志成, 陈思忠, 杨林, 等. 基于有理函数的路面不平度时域模型研究[J] . 北京理工大学学报,2009,29(9):795 − 798. [4] 尹志新, 李端芳, 唐萌, 等. 基于MATLAB的时域路面不平度仿真研究[J] . 装备制造技术,2010(4):43 − 44, 51. doi: 10.3969/j.issn.1672-545X.2010.04.018 [5] 史宏伟, 师帅兵, 李亮. 七自由度车辆悬架系统的数学建模[J] . 拖拉机与农用运输车,2009,36(4):26 − 27. doi: 10.3969/j.issn.1006-0006.2009.04.010 [6] 许伟, 高远. 基于遗传算法的汽车主动悬架LQR控制研究[J] . 计算机与数字工程,2019,47(9):2212 − 2216. doi: 10.3969/j.issn.1672-9722.2019.09.021 [7] TRUPTI P. PHALKE, ANIRBAN C M. Analysis of ride comfort and road holding of quarter car model by SIMULINK[J] . Materials Today: Proceedings,2017,4(2):2425 − 2430. doi: 10.1016/j.matpr.2017.02.093 [8] 谢俊淋, 张庆永. 基于Simulink的汽车平顺性仿真分析[J] . 机电技术,2013,36(1):14 − 18. doi: 10.3969/j.issn.1672-4801.2013.01.004 [9] LIHLE I N, ALBERT D, MOHLALAKOMA T N, et al. Heaviside based optimal control for ride comfort and actuation energy optimisation in half-car suspension systems[J] . IFAC-Papers OnLine,2017,50(2):259 − 264. doi: 10.1016/j.ifacol.2017.12.055 [10] 赵旗, 王维, 李杰, 等. 基于滤波白噪声的汽车平顺性时域建模和仿真[J] . 科学技术与工程,2016,16(27):283 − 287. doi: 10.3969/j.issn.1671-1815.2016.27.052 [11] 毕凤荣, 石纯放, 梁永勤. 悬架系统非线性减振器阻尼值变化系数对整车振动影响的研究[J] . 机械科学与技术,2017,36(9):1421 − 1427. [12] 余志生. 汽车理论[M]. 3版. 北京: 机械工业出版社, 2000. [13] 杨万桥. 基于人—车—路相互作用的沥青路面平整度评价方法研究[D]. 西安: 长安大学, 2009. [14] 刘大维, 蒋荣超, 朱龙龙, 等. 基于遗传算法的路面有理函数功率谱密度参数识别[J] . 农业工程学报,2012,28(8):128 − 133. doi: 10.3969/j.issn.1002-6819.2012.08.020 [15] 中国汽车技术研究中心. 车辆振动输入路面平度表示方法: GB 7031—1986[S]. 北京: 中国标准出版社, 1986: 11. [16] 赵珩, 卢士富. 路面对四轮汽车输入的时域模型[J] . 汽车工程,1999,21(2):112 − 117. [17] 倪晋尚. 汽车悬架的平顺性优化及仿真试验分析[D]. 南京: 南京航空航天大学, 2006. [18] 全国汽车标准化技术委员会. 汽车平顺性试验方法: GB/T 4970—2009[S]. 北京: 中华人民共和国国家质量监督检验检疫总局2009: 10. [19] 翟婉明, 黄志辉. 列车动力学的非线性数值分析方法[J] . 西南交通大学学报,1991(1):82 − 90. -
下载:
点击查看大图
图(11) / 表(2)
计量
- 文章访问数: 255
- HTML全文浏览量: 287
- PDF下载量: 84
- 被引次数: 0
