Trajectory tracking control of micro positioning platform based on dynamic sliding mode
-
摘要:
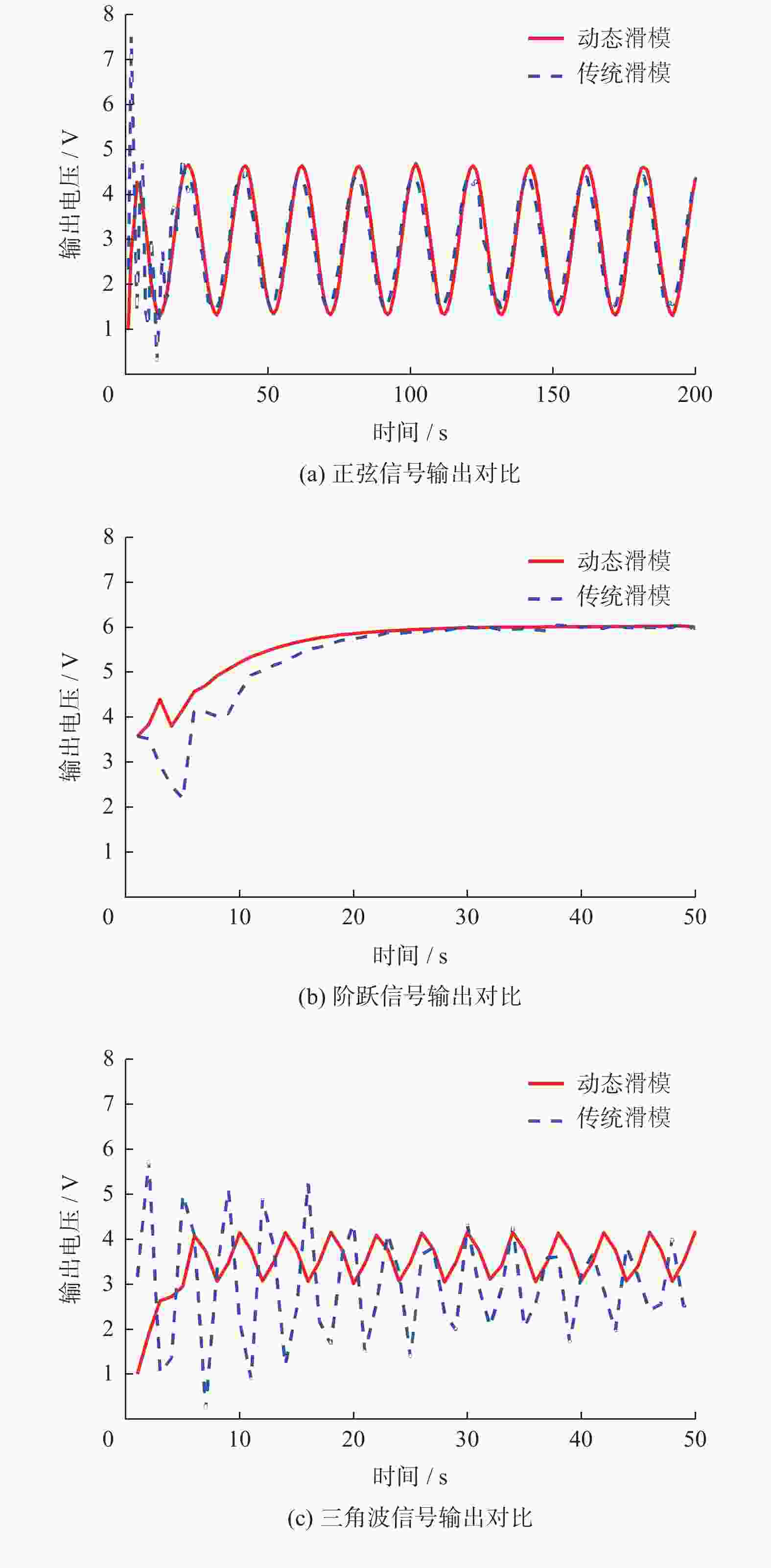
音圈电机驱动的微定位平台作为高精密度运动平台，被广泛应用于精密加工、微机电等领域. 针对音圈电机驱动的微定位平台的高精度平稳跟踪控制问题，结合归一法和理论建模的参数建立具有参数不确定性的二阶微分方程数学模型，以柔性机构实际位移作为输入，平台控制率作输出；鉴于模型参数不确定的特点，通过建立误差的二阶滑模面，提出基于动态滑模的微定位平台跟踪控制，通过李雅普诺夫稳定性理论获得系统稳定的结论. 通过平台试验对比分析提出的控制算法，结果表明提出的动态滑模控制算法在保证较小抖振的前提下，都能完成轨迹跟踪，跟踪精度比传统滑模提高13.4%和4%，且跟踪更平稳，具有良好的工程前景.
Abstract:As a high-precision motion platform, the micro positioning platform driven by the voice coil motor is widely used in precision machining, micro-electromechanical and other fields. Aiming at the high-precision and stable tracking control problem of the micro positioning platform driven by the voice coil motor, combining normalization method with theoretical modeling parameters, a mathematical model of second-order differential equation with parameter uncertainties was established, and the actual displacement of the flexible mechanism was taken as input and the platform control rate was taken as output. In view of the uncertain characteristics of the model parameters, the second-order sliding mode surface of the error was established to propose tracking control of micro positioning platform based on dynamic sliding mode, and the conclusion of system stability through Lyapunov's stability theory was obtained. The proposed control algorithm was analyzed by platform test comparison, the results show that the proposed dynamic sliding mode control algorithm can complete the trajectory tracking with less chatter. The tracking accuracy of the algorithm has improved by 13.4% and 4% compared to traditional sliding mode control, which has a smoother tracking and a good engineering prospects.
-
Key words:
- micro positioning platform /
- dynamic sliding mode /
- motor driven /
- trajectory tracking
-
图 5 不同控制器作用下轨迹跟踪变化曲线
Figure 5. Trajectory tracking variation under different controllers
表 1 不同信号跟踪误差
Table 1. Different signal tracking error
信号种类 动态滑模 传统滑模 最大稳态
误差/mm均方根稳
态误差/mm最大稳态
误差/mm均方根稳
态误差/mm正弦 0.1900 0.0475 0.5467 0.1067 阶跃 0.0245 0.0295 0.1243 0.0308 三角波 0.2013 0.0538 2.0462 0.9752 
下载: 导出CSV
-
[1] WU Z Y, XU Q S. Design, optimization and testing of a compact XY parallel nanopositioning stage with stacked structure[J] . Mechanism & Machine Theory,2018,126:171 − 188. [2] 田延岭, 包亚洲, 王福军, 等. 音圈电机驱动的柔性定位平台设计与控制[J] . 天津大学学报(自然科学与工程技术版),2017,50(10):1070 − 1076. [3] 柴嘉伟, 贵献国. 音圈电机结构优化及应用综述[J] . 电工技术学报,2021,36(6):1113 − 1125. [4] 余江. 压电驱动微定位平台的控制及评价研究[D]. 重庆: 重庆大学, 2019. [5] 潘炜. 压电驱动微定位平台迟滞动态建模与控制方法研究[D]. 长春: 吉林大学, 2020. [6] 周淼磊, 张敬爱, 赵宇, 等. 压电微定位平台神经网络与专家模糊复合控制方法[J] . 控制与决策,2018,33(1):95 − 100. [7] 高为炳. 变结构控制理论基础[M]. 北京: 中国科学技术出版社, 1990. [8] 刘金琨. 滑模变结构控制Matlab仿真[M]. 北京: 清华大学出版社, 2012. [9] 蓝益鹏, 王靖腾, 刘欣. 可控励磁直线同步电动机的全局积分Terminal滑模控制[J] . 控制理论与应用,2019,36(6):931 − 938. doi: 10.7641/CTA.2018.80198 [10] 张瑶, 马广富, 郭延宁, 等. 一种多幂次滑模趋近律设计与分析[J] . 自动化学报,2016,42(3):466 − 472. [11] 田福庆, 姜尚, 梁伟阁. 含齿隙弹载舵机的全局反步模糊自适应控制[J] . 自动化学报,2019,45(6):1177 − 1185. [12] 许叙遥, 林辉. 基于动态滑模控制的永磁同步电机位置速度一体化设计[J] . 电工技术学报,2014,29(5):77 − 83. doi: 10.3969/j.issn.1000-6753.2014.05.011 [13] 朱庆华, 董瑞琦, 马广富. 基于动态滑模控制的挠性航天器姿态控制[J] . 控制理论与应用,2018,35(10):1430 − 1435. doi: 10.7641/CTA.2018.70863 [14] 何雄, 张农, 孔国玲. 基于动态滑模算法的AMT选换挡电机控制[J] . 中国机械工程,2016,27(10):1414 − 1419. doi: 10.3969/j.issn.1004-132X.2016.10.023 -
下载:
点击查看大图
计量
- 文章访问数: 374
- HTML全文浏览量: 183
- PDF下载量: 56
- 被引次数: 0
