Trajectory tracking control of Mecanum wheel omnidirectional mobile robot based on power reaching law
-
摘要:
针对基于一般滑模的麦克纳姆轮全向移动机器人在轨迹跟踪过程中收敛速度慢、耗时长及控制存在抖振等问题,提出一种利用多幂次趋近律实现系统快速收敛的滑模控制. 通过控制4个麦克纳姆轮的角速度实现机器人3个自由度的位置变化,完成3输入4输出的控制,根据所建的数学模型,使用多幂次趋近律在系统趋近滑模面的不同阶段进行针对性调节保证收敛速度,用双曲正切函数替换趋近律中的符号函数改善抖振问题,利用Lyapunov理论证明3输入4输出控制系统的稳定性,最后 通过仿真验证所提出算法的有效性.
Abstract:Aiming at problems of slow convergence and long time consuming in trajectory tracking, and chattering problem exists in the control of Mecanum wheel omnidirectional mobile robot based on general sliding mode, a sliding mode control method was proposed to realize the rapid convergence of the system by using the multi power reaching law. The position change of three degrees of freedom of robot was realized by controlling the angular velocity of four Mecanum wheels, and the control of three inputs and four outputs was completed. According to the mathematical model established, the multi power reaching law was used to adjust the convergence speed at different stages of the system approaching sliding mode surface, and the hyperbolic tangent function was used to replace the sign function in the reaching law to improve the chattering problem. The stability of the three inputs and four outputs control system was proved by Lyapunov theory. Finally, the control effect of the proposed algorithm was illustrated by simulation and comparison analysis.
-
Key words:
- Mecanum wheel /
- trajectory tracking /
- sliding mode control /
- multi power reaching law
-
表 1 MP-SMC仿真参数设置表
Table 1. Simulation parameters setting table of MP-SMC
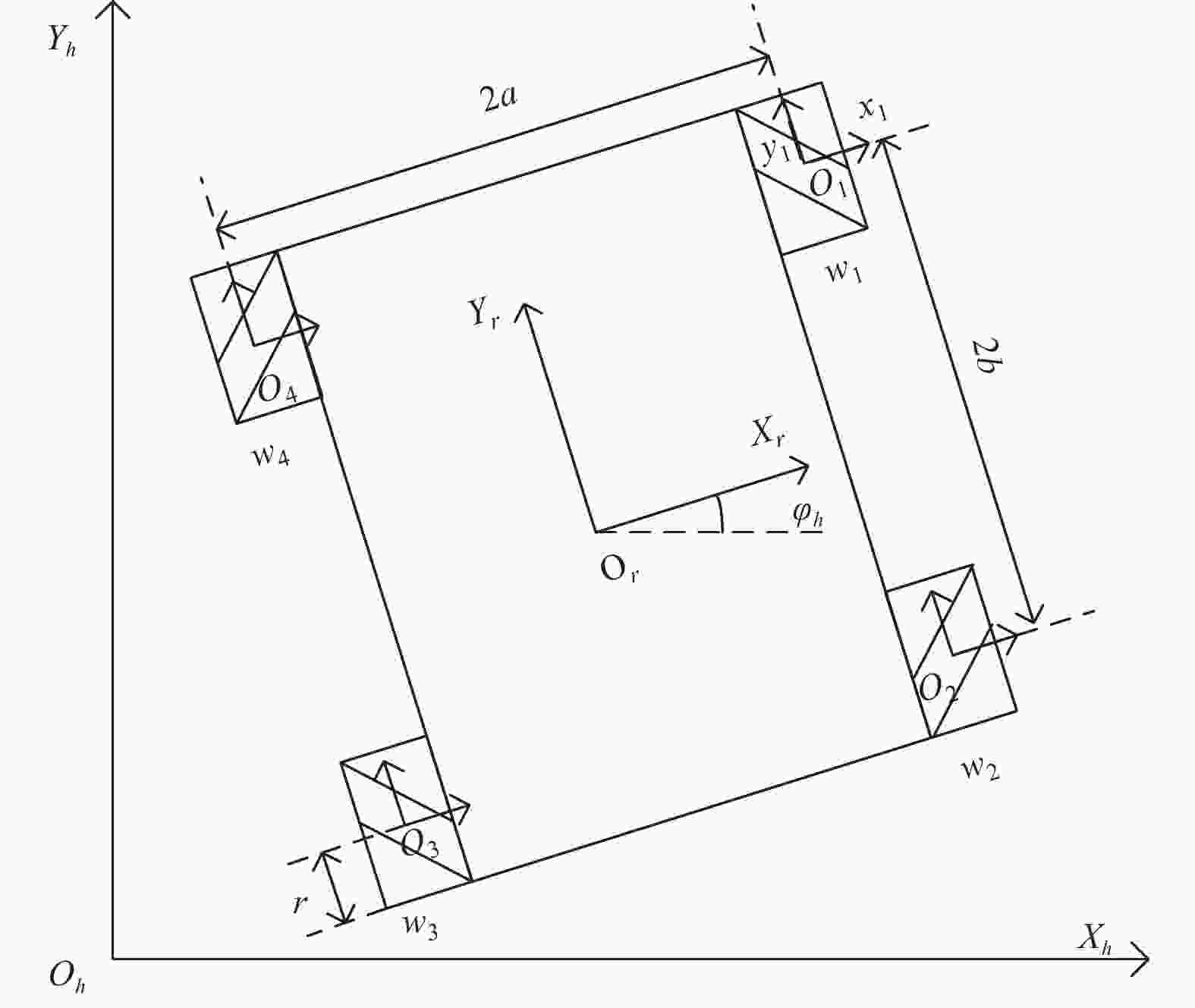
参数 值 a/m 0.25 b/m 0.35 r/m 0.05 ${I_0}/({\rm{kg}}{\rm{\cdot} }{ {\rm{m} }^{\rm{2} } })$ 0.09 ${\eta _0}/({\rm{N}}{\rm{\cdot m\cdot s\cdot rad^{-1} } })$ 0.2 $ \alpha $ 10 $ \beta $ 0.2 $ \delta $ diag{12,12,12} $\lambda $ diag{10,10,10} $ \sigma $ diag{100,100,100} $ \varepsilon $ diag{30,30,30} k diag{30,30,30} -
[1] TLALE N , DE VILLIERS M. Kinematics and dynamics modelling of a Mecanum wheeled mobile platform[C]// Proceedings of International Conference on Mechatronics & Machine Vision in Practice. Auckland: IEEE, 2009: 657-662. [2] 方玉发. 基于麦克纳姆轮的重载AGV关键技术研究与应用[D]. 杭州: 浙江大学, 2019. [3] 黄群军, 谢志江. 改进A*算法的麦克纳姆轮AGV路径规划[J/OL]. 机械科学与技术: 1-7[2021-06-16]. https://doi.org/10.13433/j.cnki.1003-8728.20200189. [4] HOU L F, ZHOU F Y, KIM K, et al. Practical model for energy consumption analysis of omnidirectional mobile robot[J] . Sensors,2021,21(5):1800 − 1812. doi: 10.3390/s21051800 [5] ALAKSHENDRA V, CHIDDARWAR S S. Adaptive robust control of Mecanum-wheeled mobile robot with uncertainties[J] . Nonlinear Dynamics,2017,87(4):2147 − 2169. doi: 10.1007/s11071-016-3179-1 [6] MUIR P F . Kinematic modeling for feedback control of an omnidirectional wheeled mobile robot[M]//COX I J, WILFONG G T. Autonomous robot vehicles. New York: Springer, 1987: 25−31. [7] SUN Z, XIE H, ZHENG J C, et al. Path-following control of Mecanum-wheels omnidirectional mobile robots using nonsingular terminal sliding mode[J] . Mechanical Systems and Signal Processing,2021, 147:107128. [8] MALAYJERDI E , KALANI H , MALAYJERDI M . Self-tuning fuzzy pid control of a four-mecanum wheel omni-directional mobile platform[C]// Proceedings of the 26th Iranian Conference on Electrical Engineering (ICEE). Mashan: Sadjad University, 2018: 816-820. [9] TSAI C C, TAI F C , LEE Y R . Motion controller design and embedded realization for Mecanum wheeled omnidirectional robots[C]// Proceedings of the 8th World Congress on Intelligent Control and Automation. Taipei: IEEE, 2011: 546-551. [10] 王勃, 王天擎, 于泳, 等. 感应电机电流环非线性积分滑模控制策略[J]. 电工技术学报, 2021(10): 2039-2048 [11] QIAO Z W, SHI T N, WANG Y D, et al. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor[J] . IEEE Transactions on Industrial Electronics,2013,60(2):710 − 719. doi: 10.1109/TIE.2012.2206359 [12] 吕德刚, 李子豪. 表贴式永磁同步电机改进滑模观测器控制[J]. 电机与控制学报, 2021(10): 58-66. [13] 张瑶, 马广富, 郭延宁, 等. 一种多幂次滑模趋近律设计与分析[J] . 自动化学报,2016,42(3):466 − 472. [14] YUAN Z Y, TIAN Y X, YIN Y F, et al. Trajectory tracking control of a four Mecanum wheeled mobile platform: An extended state observer-based sliding mode approach[J] . IET Control Theory and Applications,2019,14(3):415 − 426. [15] 王明明, 朱莹莹, 张磊, 等. 麦克纳姆轮驱动的移动机器人自适应滑模控制器设计[J] . 西北工业大学学报,2018,36(4):627 − 635. doi: 10.3969/j.issn.1000-2758.2018.04.004 [16] 张星. 基于麦克纳姆轮的全向AGV运动控制技术研究[D]. 重庆: 重庆大学, 2016. [17] SLOTINE J , LI W P . Applied nonlinear control[M]. Shanghai: China Machine Press, 1991. -





 下载:
下载: