Dynamic modeling and simulation of 2UPR/UPS/UP parallel mechanism
-
摘要:
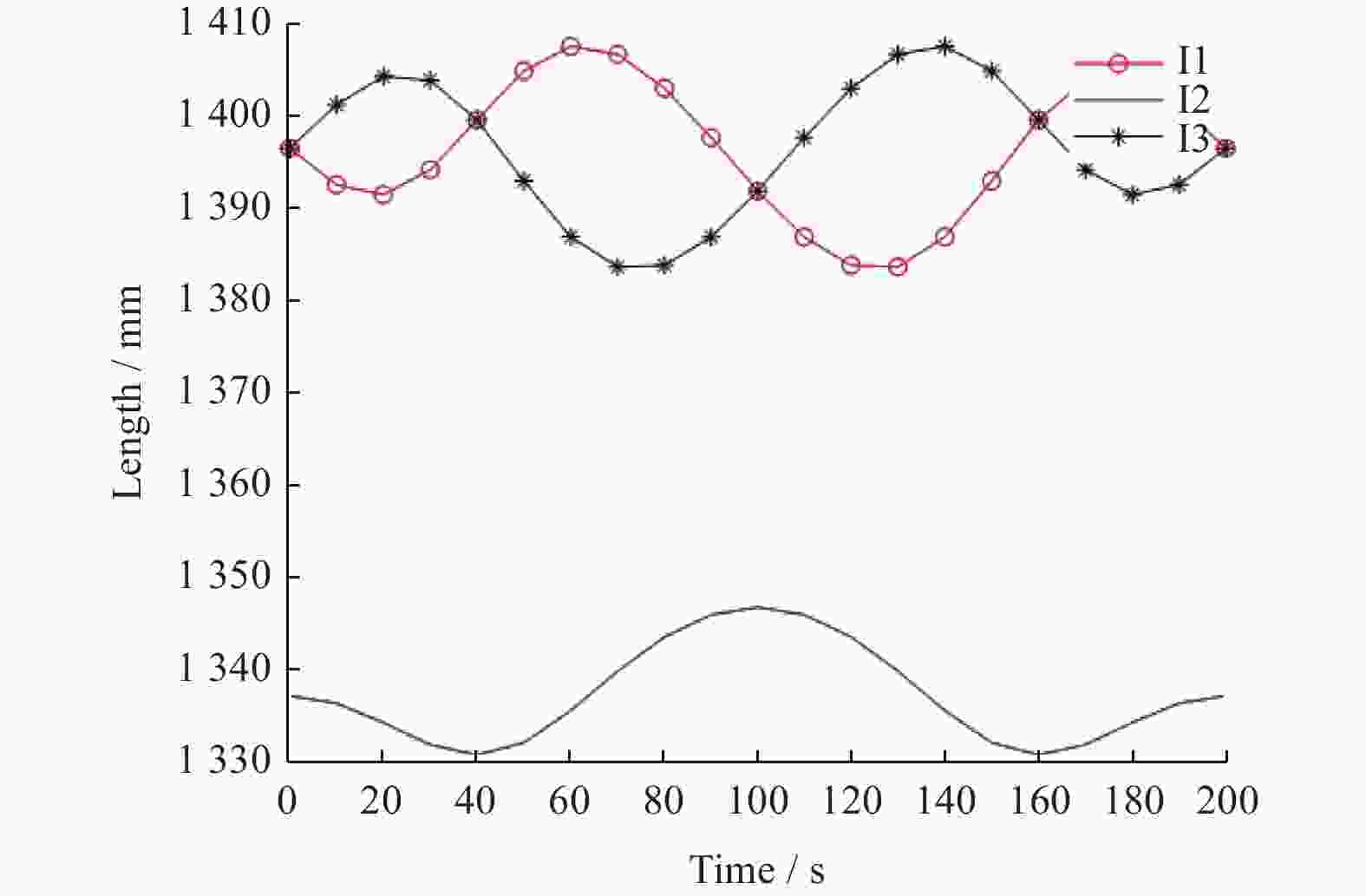
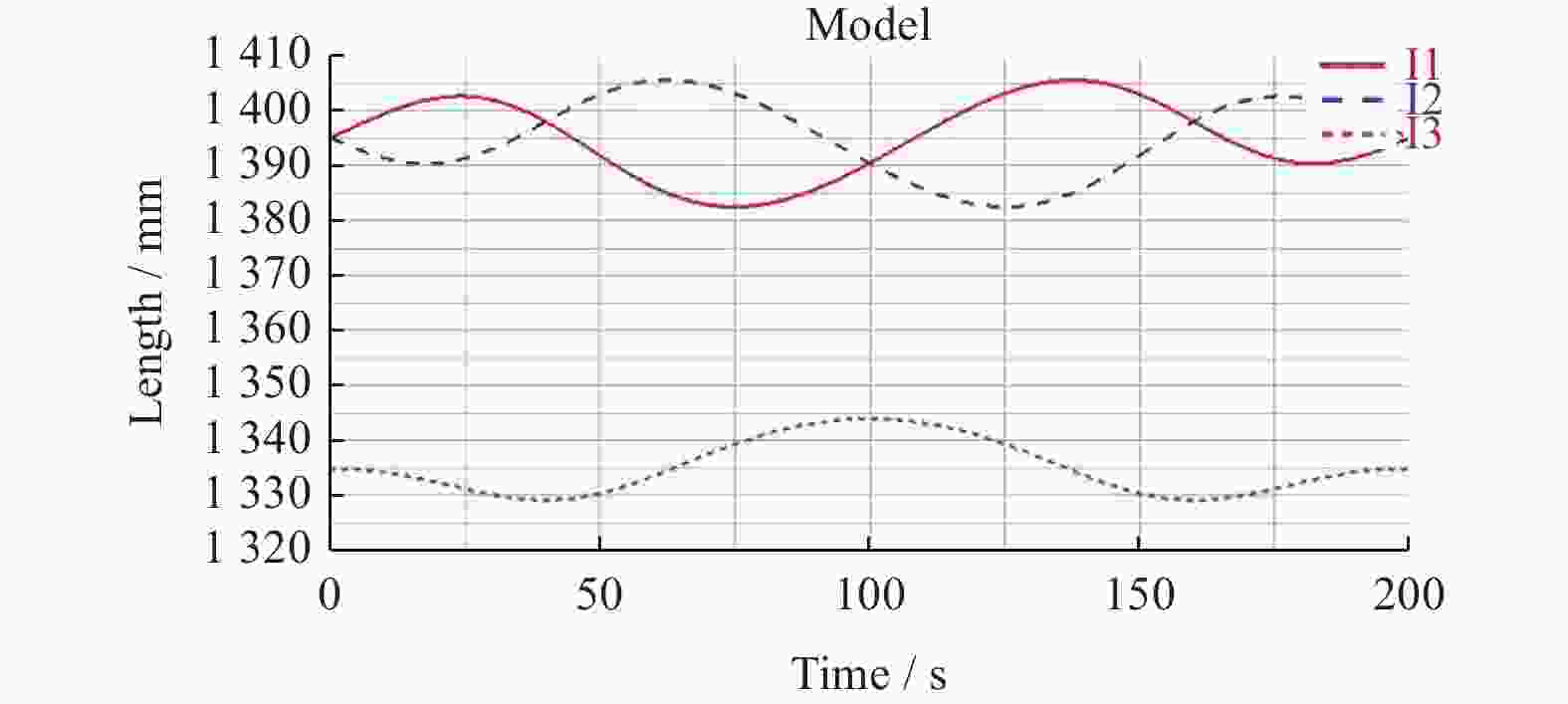
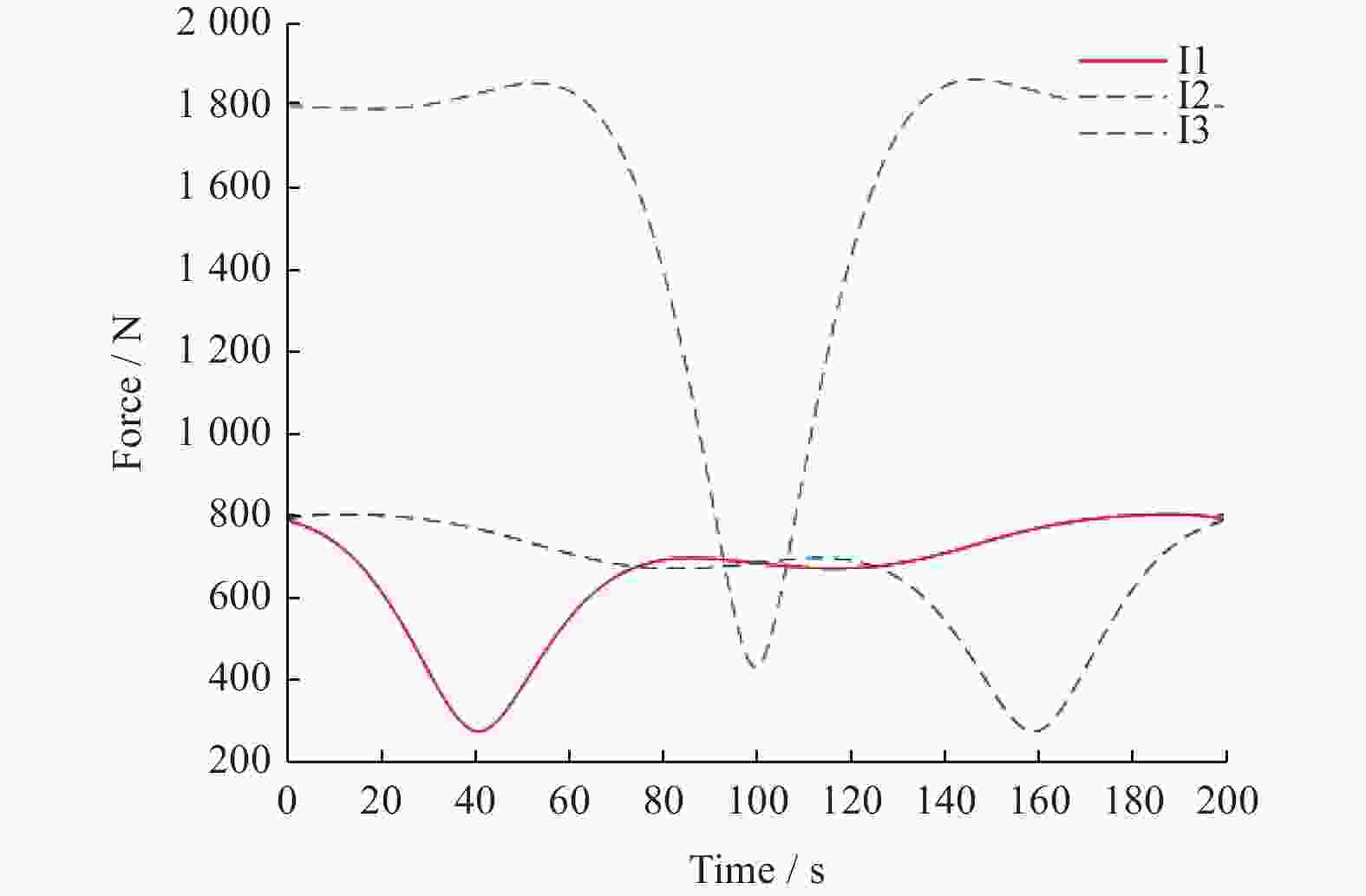
以一种具有空间三自由度的2UPR/UPS/UP冗余并联机构为研究对象，根据机构的约束条件建立各支链的闭环约束矢量方程，求得机构的位置反解并得到雅可比矩阵. 根据运动学分析，得到3个驱动支链的变化规律，方便实现对机构的位姿控制. 在此基础上，利用虚功原理对机构的动力学进行分析，建立该机构的动力学模型. 最后，在典型工况下对机构的运动学和动力学分别进行Matlab算例仿真与Adams样机仿真，通过对比仿真结果验证运动学和动力学模型的正确性. 该方法为并联机构的设计和控制奠定理论基础，同时适用于类似机构的研究与分析.
Abstract:The 2UPR/UPS/UP redundant parallel mechanism (PM) with three degrees of freedom was taken as the research object. According to constraint conditions of this PM, the inverse solution of position and the Jacobian matrix were solved by establishing closed-loop vector equation of each branch. Based on kinematics analysis, the regular pattern of three driving branches was obtained to be convenient to achieve the position and orientation control of this PM. Based on the above conditions, the dynamics of this PM was developed by using the virtual work principle, and the dynamics model was established. Finally, the simulation of mechanism kinematics and dynamics were implemented by applying Matlab and Adams software under typical working conditions. The simulation results can testify the validity of the kinematics and dynamics model. The method lays a theoretical foundation for the design and control of this PM and is fit for the research and analysis of similar mechanisms.
-
Key words:
- parallel mechanism /
- kinematics /
- inverse dynamics /
- virtual work principle
-
图 2 Matlab计算得到的驱动杆长变化曲线
Figure 2. Variation curve of driving rod length calculated by Matlab
图 3 Adams仿真得到的驱动杆长变化曲线
Figure 3. Variation curve of driving rod length obtained by Adams simulation
图 5 Matlab计算得到的驱动力变化曲线
Figure 5. Variation curve of driving force calculated by Matlab
图 6 Adams仿真得到的驱动力变化曲线
Figure 6. Variation curve of driving force obtained by Adams simulation
表 1 几何和惯性参数
Table 1. Geometric and inertial parameters
参数 数值 单位 $a$ 625 mm $b$ 250 mm ${m_C}$ 85 kg ${m_{li}}(i = 1,2,3)$ 132 kg ${{\boldsymbol{I}}_C}$ Diag[36.2,36.2,0.2] kg·${{\rm{m}}^2}$ ${{\boldsymbol{I}}}_{li}^{’}(i=1,2,3)$ Diag[5.6,5.6,0.077] kg·${{\rm{m}}^2}$ 
下载: 导出CSV
-
[1] SU H J, DIETMAIER P, MCCARTHY J M. Trajectory planning for constrained parallel manipulators[J] . Journal of Mechanical Design,2003,125(4):709 − 716. [2] ANGELES J. The qualitative synthesis of parallel manipulators[J] . Journal of Mechanical Design,2004,126(4):617 − 624. [3] HUANG Z, LI Q C. Type synthesis of symmetrical lower-mobility parallel mechanisms using the constraint-synthesis method[J] . The International Journal of Robotics Research,2003,22(1):59 − 79. [4] LI Q C, HERVE J M. Type synthesis of 3-DOF RPR-equivalent parallel mechanisms[J] . IEEE Transactions on Robotics,2014,30(6):1333 − 1343. [5] CHAI X X, WANG M, XU L M, et al. Dynamic modeling and analysis of a 2PRU-UPR parallel robot based on screw theory[J] . IEEE Access,2020,8:78868 − 78878. doi: 10.1109/ACCESS.2020.2989783 [6] QAZANI MRC, PEDRAMMEHR S, RAHMANI A, et al. Kinematic analysis and workspace determination of hexarot-a novel 6-DOF parallel manipulator with a rotation-symmetric arm system[J] . Journal of Robotic Systems,2015,33:1686 − 1703. [7] YANG C F, ZHENG S T, JIN J, et al. Forward kinematics analysis of parallel manipulator using modified global Newton-Raphson method[J] . Journal of Central South University of Technology,2010,17(6):1264 − 1270. doi: 10.1007/s11771-010-0630-1 [8] MA Z S, YU S H, HAN Y, et al. Zeroing neural network for bound-constrained time-varying nonlinear equation solving and its application to mobile robot manipulators[J] . Neural Computing and Applications,2021,33(21):14231 − 14245. doi: 10.1007/s00521-021-06068-6 [9] KUCUCK S, BINGUL Z. The inverse kinematics solutions of fundamental robot manipulators with offset wrist[J] . IEEE International Conference on Mechatronics,2005:197 − 202. [10] BI Z M, JIN Y. Kinematic modeling of exechon parallel kinematic machine[J] . Robotics and Computer-Integrated Manufacturing,2011,27(1):186 − 193. doi: 10.1016/j.rcim.2010.07.006 [11] LI M, HUANG T, CHETWYND D G, et al. Forward position analysis of the 3DOF module of the trivariant: A 5-DOF reconfigurable hybrid robot[J] . Journal of Mechanical Design,2006,128(1):319 − 322. doi: 10.1115/1.2125971 [12] ZHANG D S, XU Y D, YAO J T, et al. Kinematics modelling and optimization design of a 5-DOF hybrid manipulator[J] . International journal of robotics& automation,2018,33(4):407 − 417. [13] 陈修龙, 陈林林, 梁小夏. 4自由度冗余驱动并联机构运动学和工作空间分析[J] . 农业机械学报,2014,45(8):307 − 313. doi: 10.6041/j.issn.1000-1298.2014.08.049 [14] XIN G Y, DENG H, ZHONG G L. Closed-form dynamics of a 3-DOF spatial parallel manipulator by combining the Lagrangian formulation with the virtual work principle[J] . Nonlinear Dynamics,2016,86(2):1329 − 1347. doi: 10.1007/s11071-016-2967-y [15] LIU S Z, ZHU Z C, SUN Z P, et al. Kinematics and dynamics analysis of a three-degree-of-freedom parallel manipulator[J] . Journal of Central South University,2014,21:2660 − 2666. [16] XIE S L, HU K M, LIU H T, et al. Dynamic modeling and performance analysis of a new redundant parallel rehabilitation robot[J] . IEEE Access,2020,8:222211 − 25. doi: 10.1109/ACCESS.2020.3043429 [17] 王潇剑, 吴军, 岳义, 等. 3自由度并联机构的动力学性能评价[J] . 清华大学学报,2019,59(10):838 − 846. [18] WU P D, XIONG H G, KONG J Y. Dynamic analysis of 6-SPS parallel mechanism[J] . International Journal of Mechanics and Materials Design,2012,8(2):121 − 128. doi: 10.1007/s10999-012-9181-y [19] GALLARDO J, RICO J M, FRISOLI A, et al. Dynamics of parallel manipulators by means of screw theory[J] . Mechanism and Machine Theory,2003,38(11):1113 − 1131. -
下载:
点击查看大图
计量
- 文章访问数: 427
- HTML全文浏览量: 162
- PDF下载量: 49
- 被引次数: 0
