Precision allocation optimization design of five axis machine tool based on second-order moment error model
-
摘要:
在机床精度优化设计过程中，传统精度分配中往往将误差视为常量，而忽略误差的分布情况. 针对此问题，在分析传统精度分配方法基础上，提出一种基于二阶矩误差模型的五轴数控机床精度优化设计方法. 定义二阶矩阵运算规则，用二阶矩阵表达机床精度指标，建立带分布的五轴数控机床误差模型，应用遗传算法对精度指标进行多目标优化求解，得到Pareto最优解集. 以C100P五轴数控机床为例，验证本优化设计方法的可行性. 与传统精度分配方法相比，在保证机床精度要求前提下，新方法能够降低机床装配成本.
Abstract:During the process of machine tool precision optimization design, it often regards the error as constant and ignores error distribution in the traditional precision allocation. Based on the analysis of traditional precision allocation method, a precision allocation optimization design of five axis machine tool based on second-order moment error model was proposed to this. The second-order matrix operation rules were defined and the machine tool accuracy index was expressed by the second-order matrix, the error model of five axis machine tool with distribution was established and the multi-objective optimization of the accuracy index was solved by genetic algorithm to obtain the Pareto optimal solution set. Taking C100P five axis machine tool as an example, the feasibility of this optimization design method was verified. Compared with the traditional accuracy allocation method, it can reduce the assembly cost on the premise of ensuring the accuracy requirements of the machine tool.
-
图 4
$ y\left( i \right) $ 频率直方分布及正态分布拟合曲线Figure 4. Fitting curve of frequency square distribution and normal distribution for
$ y\left( i \right) $ 表 1 二阶矩运算规则
Table 1. Second-order moment operation rules
运算类型 二阶矩运算表达式 常数项与误差项加法 ${c } + \Delta x = \left( {a,{b^2} } \right) + \left( {c,0} \right)$ 常数项与误差项乘法 ${c } {\text{•} } \Delta x = \left( {a,{b^2} } \right) {\text{•} } \left( {c,0} \right)$ 误差项与误差项加法 $ \Delta {x_1} + \Delta {x_2} = \left( {{a_{\text{1}}},{b_{\text{1}}}^2} \right) + \left( {{a_{\text{2}}},{b_{\text{2}}}^2} \right) $ 误差项与误差项乘法 $\Delta {x_{\text{1} } } {\text{•} } \Delta {x_{\text{2} } } = \left( { {a_{\text{1} } },{b_{\text{1} } }^2} \right) {\text{•} } \left( { {a_{\text{2} } },{b_{\text{2} } }^2} \right)$ 
下载: 导出CSV
表 2 误差二阶矩乘法运算部分结果
Table 2. Partial results of error second-order moment multiplication
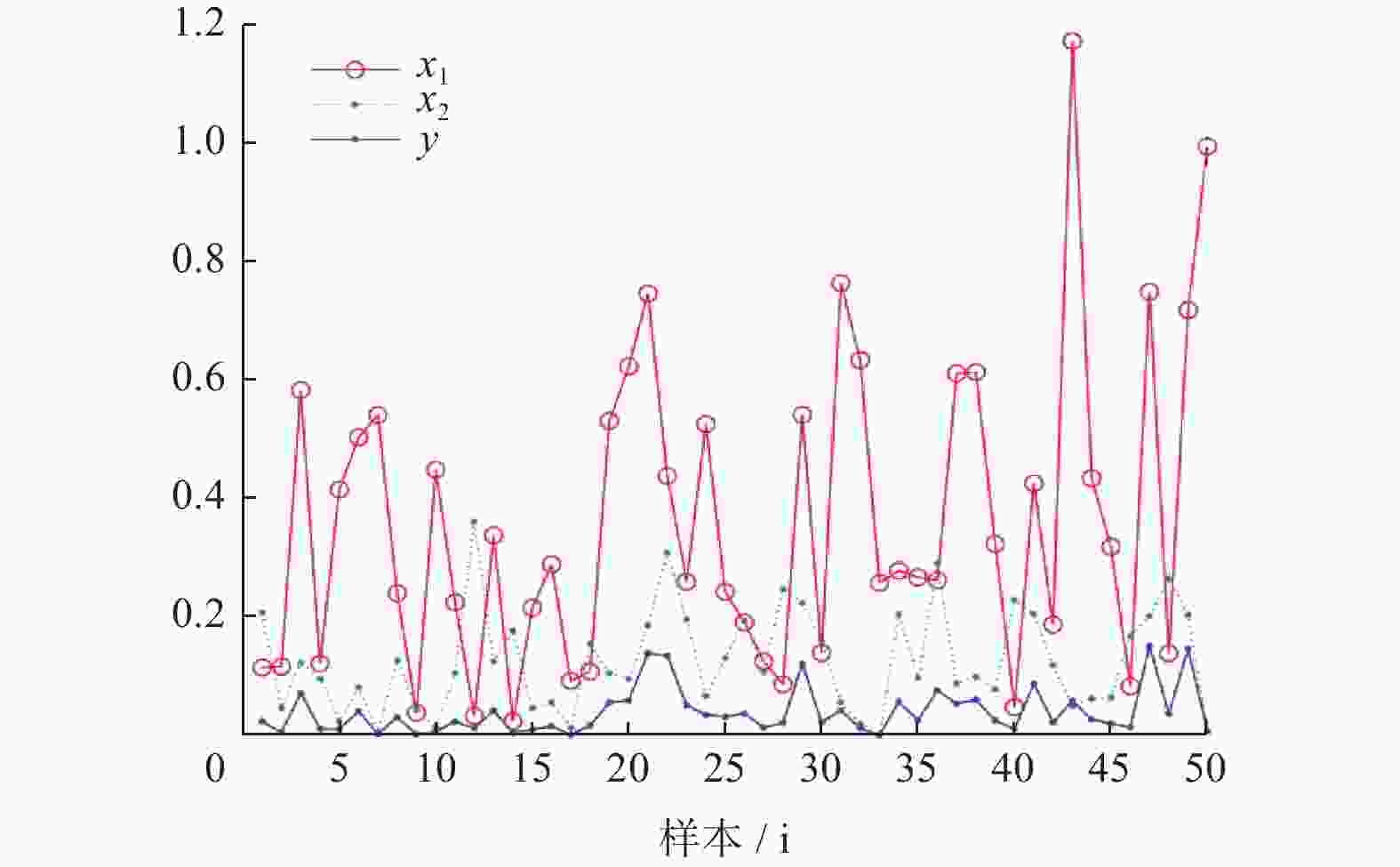
i 1 2 3 4 5 6 7 $ \phi ({x_{\text{1}}}\left( i \right)){\text{/mm}} $ −0.0206 0.0509 0.0049 0.0588 −0.0062 −0.0202 −0.0083 $ \phi ({x_{\text{2}}}\left( i \right)){\text{/mm}} $ 0.0902 0.0976 0.0965 0.1049 0.1099 0.0986 0.1117 $ \phi (y\left( i \right)){\text{/mm}} $ −0.0019 0.0050 0.0005 0.0062 −0.0007 −0.0020 −0.0009
下载: 导出CSV
表 3 C100P五轴数控机床精度指标
Table 3. Accuracy index of C100P five axis machine tool
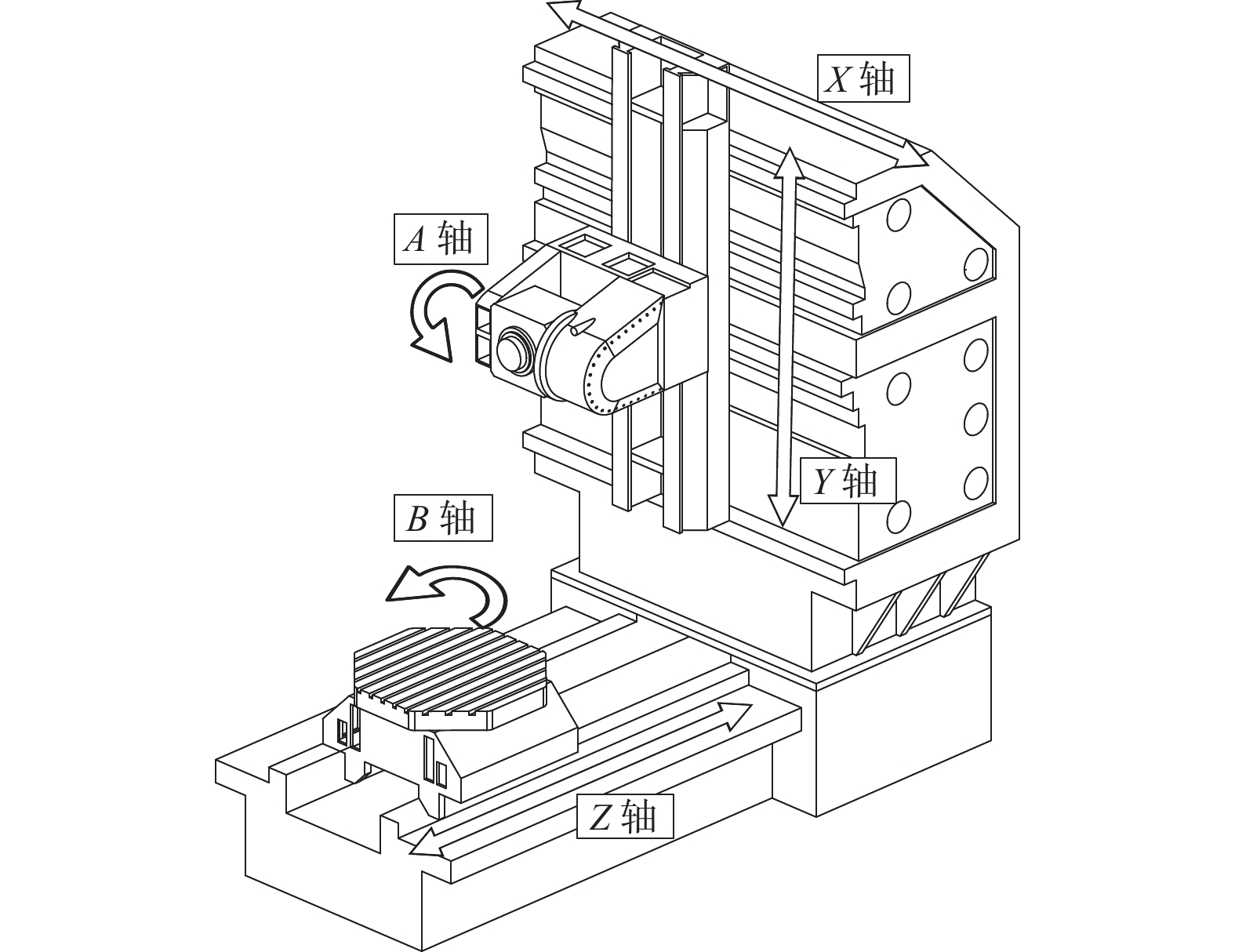
序号 变量表达式 变量含义 误差类型 1 $ \Delta {\ell _X} = [{u_{\Delta {\ell _X}}},{o_{\Delta {\ell _X}}}] $ X直线轴轴线运动直线度 沿垂直X轴平动 2 $ \Delta {\ell _Y} = [{u_{\Delta {\ell _Y}}},{o_{\Delta {\ell _Y}}}] $ Y直线轴轴线运动直线度 沿垂直Y轴平动 3 $ \Delta {\ell _Z} = [{u_{\Delta {\ell _Z}}},{o_{\Delta {\ell _Z}}}] $ Z直线轴轴线运动直线度 沿垂直Z轴平动 4 $ \Delta {\theta _{YZ}} = [{u_{\Delta {\theta _{YZ}}}},{o_{\Delta {\theta _{YZ}}}}] $ YZ直线轴垂直度误差 绕X轴转动 5 $ \Delta {\theta _{XZ}} = [{u_{\Delta {\theta _{XZ}}}},{o_{\Delta {\theta _{XZ}}}}] $ XZ直线轴垂直度误差 绕Y轴转动 6 $ \Delta {\theta _{XY}} = [{u_{\Delta {\theta _{XY}}}},{o_{\Delta {\theta _{XY}}}}] $ XY直线轴垂直度误差 绕Z轴转动 7 $ \Delta {\theta _{AL}} = [{u_{\Delta {\theta _{AL}}}},{o_{\Delta {\theta _{AL}}}}] $ A轴与直线轴垂直度误差 绕Y，Z轴转动 8 $ \Delta {\theta _{BL}} = [{u_{\Delta {\theta _{BL}}}},{o_{\Delta {\theta _{BL}}}}] $ B轴与直线轴垂直度误差 绕X，Z轴转动 9 $ \Delta {\ell _{MZ}} = [{u_{\Delta {\ell _{MZ}}}},{o_{\Delta {\ell _{MZ}}}}] $ 主轴轴线与Z轴平行度 沿X，Y轴平动 10 $ {T_{\text{p}}} = [{u_{{T_{\text{p}}}}},{o_{{T_{\text{p}}}}}] $ 台面平面度 沿Z轴平动 11 $ \Delta {\theta _{PX}} = [{u_{\Delta {\theta _{PX}}}},{o_{\Delta {\theta _{PX}}}}] $ 台面与X轴运动平行度 绕Y，Z轴转动 12 $ \Delta {\theta _{PY}} = [{u_{\Delta {\theta _{PY}}}},{o_{\Delta {\theta _{PY}}}}] $ 台面与Y轴运动平行度 绕X，Z轴转动 13 $ {\varepsilon _X} = [{u_{{\varepsilon _X}}},{o_{{\varepsilon _X}}}] $ X直线轴定位精度 沿X轴平动 14 $ {\varepsilon _Y} = [{u_{{\varepsilon _Y}}},{o_{{\varepsilon _Y}}}] $ Y直线轴定位精度 沿Y轴平动 15 $ {\varepsilon _Z} = [{u_{{\varepsilon _Z}}},{o_{{\varepsilon _Z}}}] $ Z直线轴定位精度 沿Z轴平动 16 $ \Delta {\theta _A} = [{u_{\Delta {\theta _A}}},{o_{\Delta {\theta _A}}}] $ A旋转轴定位精度 绕X轴转动 17 $ \Delta {\theta _B} = [{u_{\Delta {\theta _B}}},{o_{\Delta {\theta _B}}}] $ B旋转轴定位精度 绕Y轴转动
下载: 导出CSV
表 4 各精度指标约束区间
Table 4. Constraint interval of each accuracy index
序号 变量名 下极限偏差 上极限偏差 1 $ \Delta {\ell _X} $ 0.020 mm 0.030 mm 2 $ \Delta {\ell _Y} $ 0.020 mm 0.030 mm 3 $ \Delta {\ell _Z} $ 0.014 mm 0.015 mm 4 $ \Delta {\theta _{YZ}} $ 0.005/600 mm 0.025/600 mm 5 $ \Delta {\theta _{XZ}} $ 0.005/600 mm 0.025/600 mm 6 $ \Delta {\theta _{XY}} $ 0.005/600 mm 0.025/600 mm 7 $ \Delta {\theta _{AL}} $ 0.006 mm 0.010 mm 8 $ \Delta {\theta _{BL}} $ 0.006 mm 0.010 mm 9 $ \Delta {\ell _{MZ}} $ 0.004 mm 0.020 mm 10 $ {T_{\text{p}}} $ 0.020 mm 0.020 mm 11 $ \Delta {\theta _{PX}} $ 0.025 mm 0.050 mm 12 $ \Delta {\theta _{PY}} $ 0.020 mm 0.030 mm 13 $ {\varepsilon _X} $ 0.0064/1000 mm 0.015/1000 mm 14 $ {\varepsilon _Y} $ 0.0118/1000 mm 0.015/1000 mm 15 $ {\varepsilon _Z} $ 0.0073/1000 mm 0.010/1000 mm 16 $ \Delta {\theta _A} $ 7" 10" 17 $ \Delta {\theta _B} $ 4.6" 10"
下载: 导出CSV
表 5 精度分配结果
Table 5. Precision allocation results
mm 变量名 优化前 优化后 变量名 优化前 优化后 $ \Delta {\ell _X} $ 0.021 0.022 $ \Delta {\theta _{PX}} $ 0.025 0.031 $ \Delta {\ell _Y} $ 0.022 0.024 $ \Delta {\theta _{PY}} $ 0.020 0.020 $ \Delta {\ell _Z} $ 0.014 0.015 $ {\varepsilon _X} $ 0.010/1000 0.015/1000 $ \Delta {\theta _{YZ}} $ 0.020/600 0.003/600 $ {\varepsilon _Y} $ 0.010/1000 0.013/1000 $ \Delta {\theta _{XZ}} $ 0.020/600 0.004/600 $ {\varepsilon _Z} $ 0.010/1000 0.009/1000 $ \Delta {\theta _{XY}} $ 0.030/600 0.023/600 $ \Delta {\theta _A} $ 10" 7.8" $ \Delta {\theta _{AL}} $ 0.006 0.007 $ \Delta {\theta _B} $ 10" 7.9" $ \Delta {\theta _{BL}} $ 0.006 0.007 ${p_{{t}}}$ 0.055 0.055 $ \Delta {\ell _{MZ}} $ 0.010 0.008 $ C $ 161.97元 146.71元 $ {T_{\text{p}}} $ 0.020 0.020
下载: 导出CSV
-
[1] 于涛, 李道辉, 韩义强, 等. 基于粒子群算法的公差分配优化方法[J] . 工具技术,2016,50(9):109 − 112. doi: 10.3969/j.issn.1000-7008.2016.09.042 [2] 熊珍琦, 宁汝新, 刘检华. 产品装配精度优化模型研究[J] . 系统仿真学报,2009,21(15):4616 − 4620,4624. [3] 张岩, 莫蓉. 基于灰色粒子群算法的飞机装配公差多目标优化设计[J] . 计算机集成制造系统,2014,20(8):1870 − 1878. [4] 匡兵, 黄美发, 钟艳如. 尺寸公差与形位公差混合优化分配[J] . 计算机集成制造系统,2008,14(2):398 − 402. [5] 曹衍龙. 面向制造环境的公差稳健设计方法与技术的研究[D]. 杭州: 浙江大学, 2003. [6] 马雅丽, 李阳阳. 机床导轨形位误差不确定性对加工误差的影响[J] . 组合机床与自动化加工技术,2018(3):65 − 70. [7] FATOLAHZADEH S, MEHDIZADEH R. Reliability assessment of shallow foundation stability under eccentric load using Monte Carlo and first order second moment method[J] . Geotechnical and Geological Engineering,2021(10):1 − 14. [8] 信世豪, 张立强, 李宇昊. 基于二阶矩信息的五轴数控机床几何误差建模[J] . 制造技术与机床,2021(7):59 − 64. [9] 李烁, 孟健, 潘尔顺. 装配和制造综合的公差分配优化设计[J] . 工业工程与管理,2017,22(5):102 − 106,113. [10] 施祥玲, 徐小明, 苏林林, 等. 基于NSGA-Ⅱ算法的航天产品装配公差多目标优化[J] . 上海航天(中英文),2020,37(3):121 − 125,146. -
下载:
点击查看大图
计量
- 文章访问数: 401
- HTML全文浏览量: 230
- PDF下载量: 42
- 被引次数: 0
