Active control of workspace noise based on ChFxLMS algorithm
-
摘要:
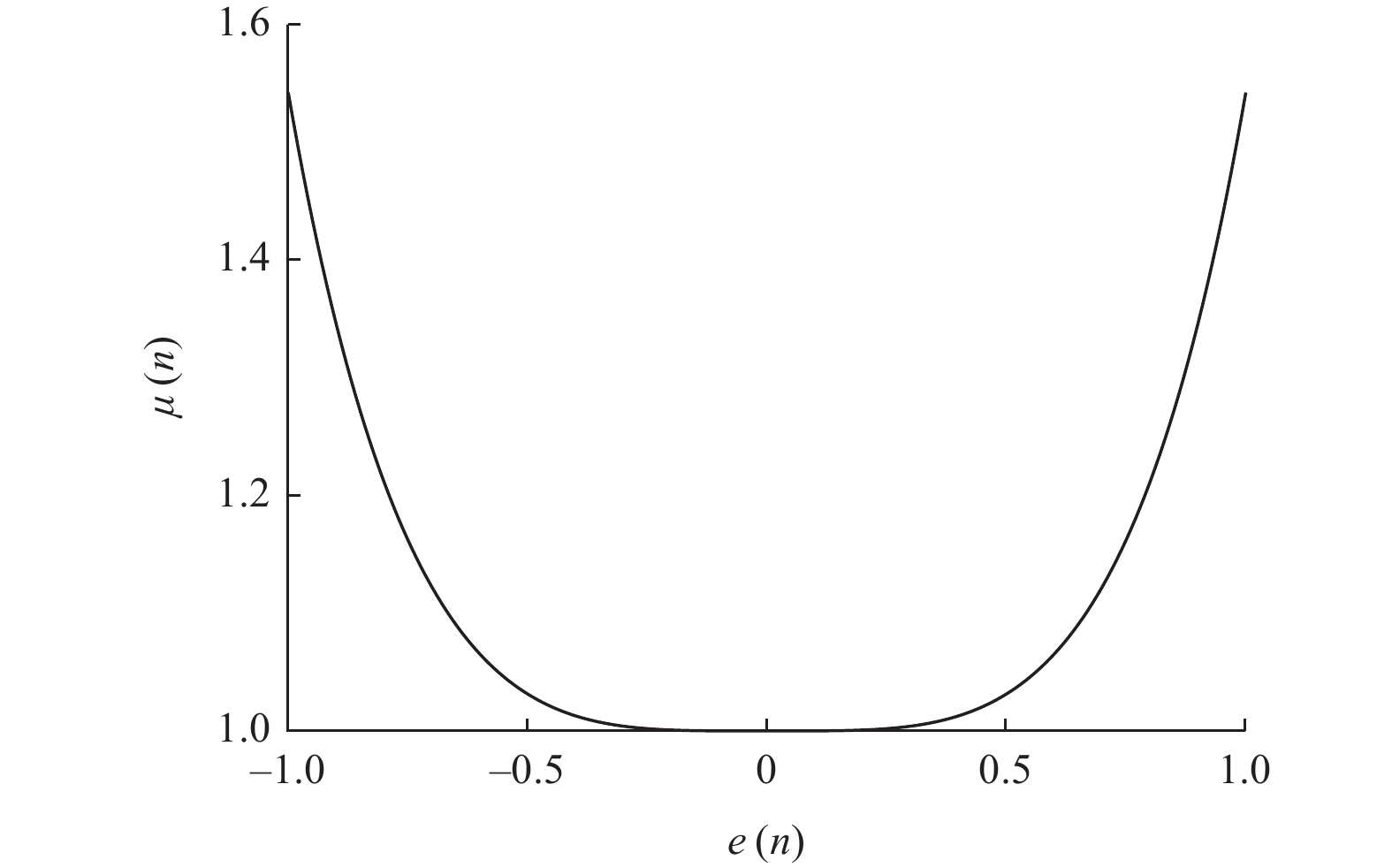
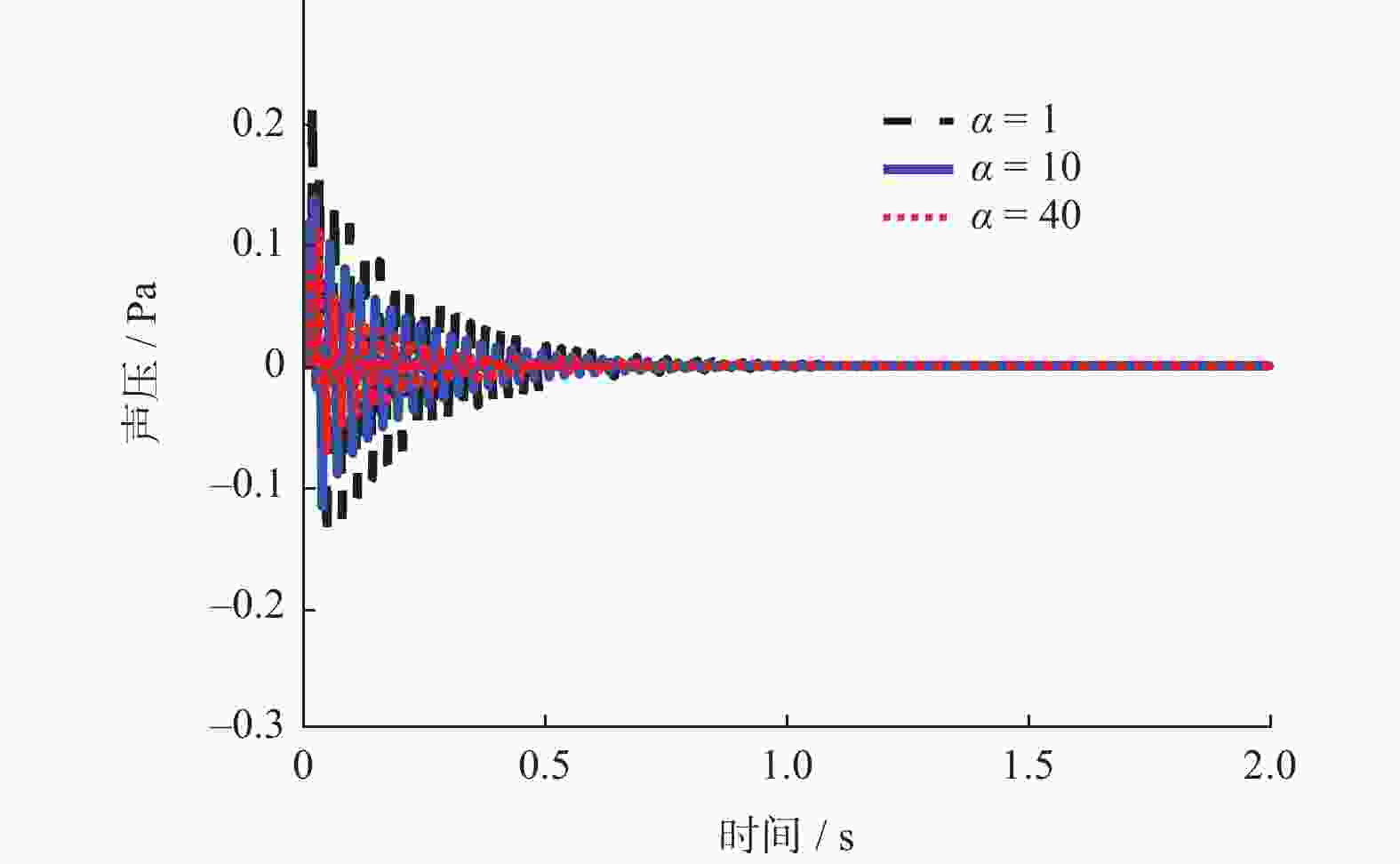
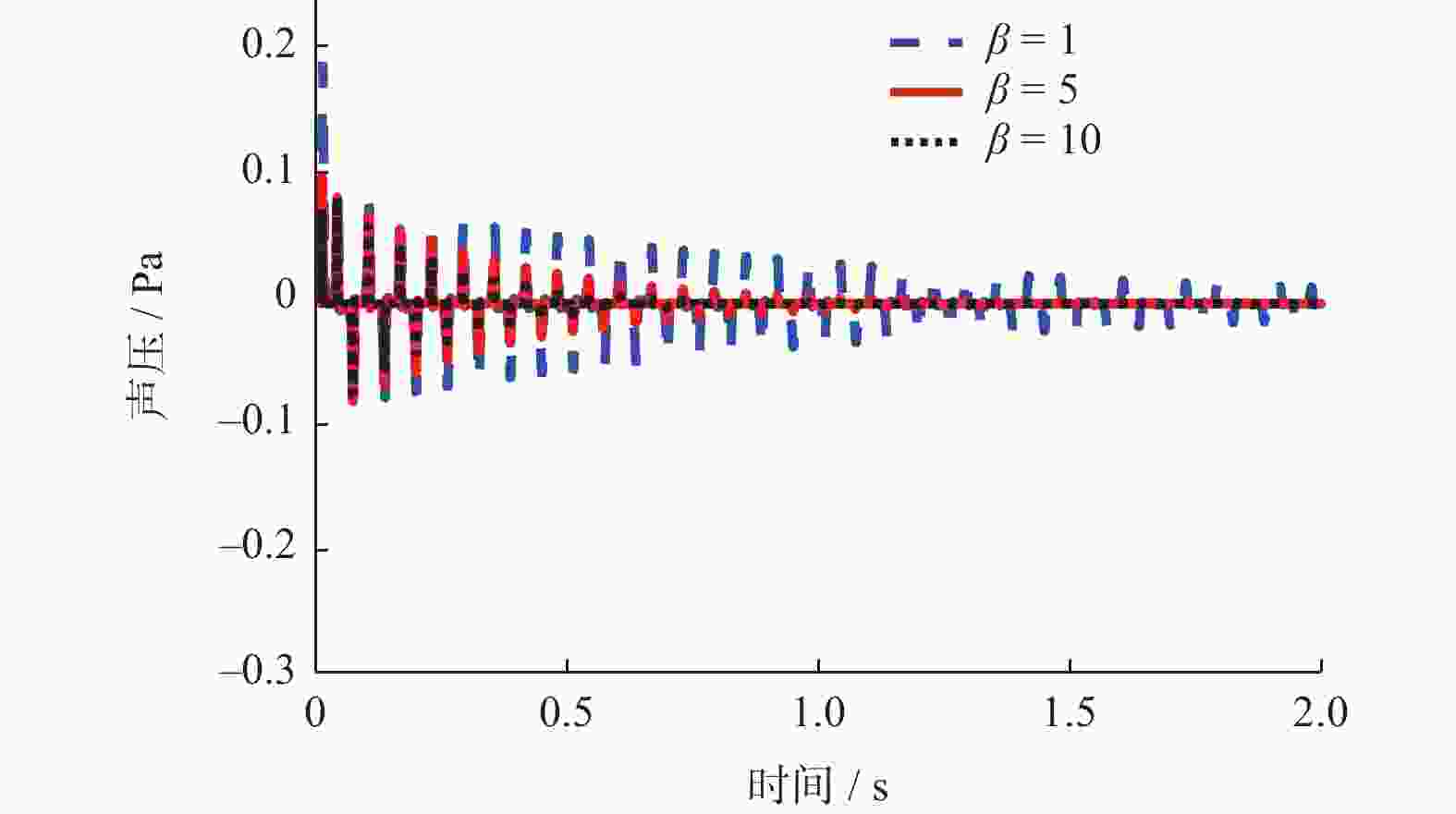
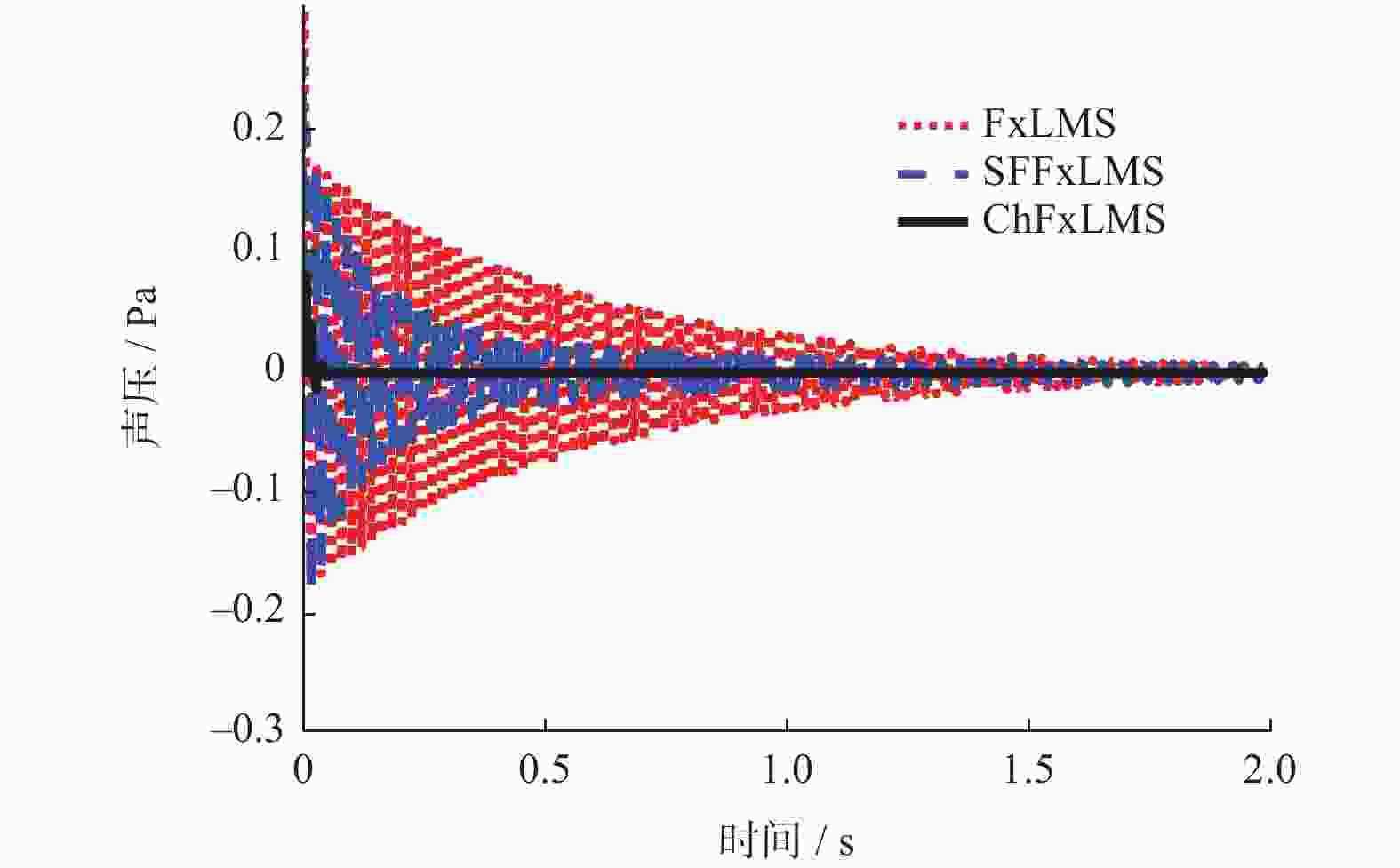
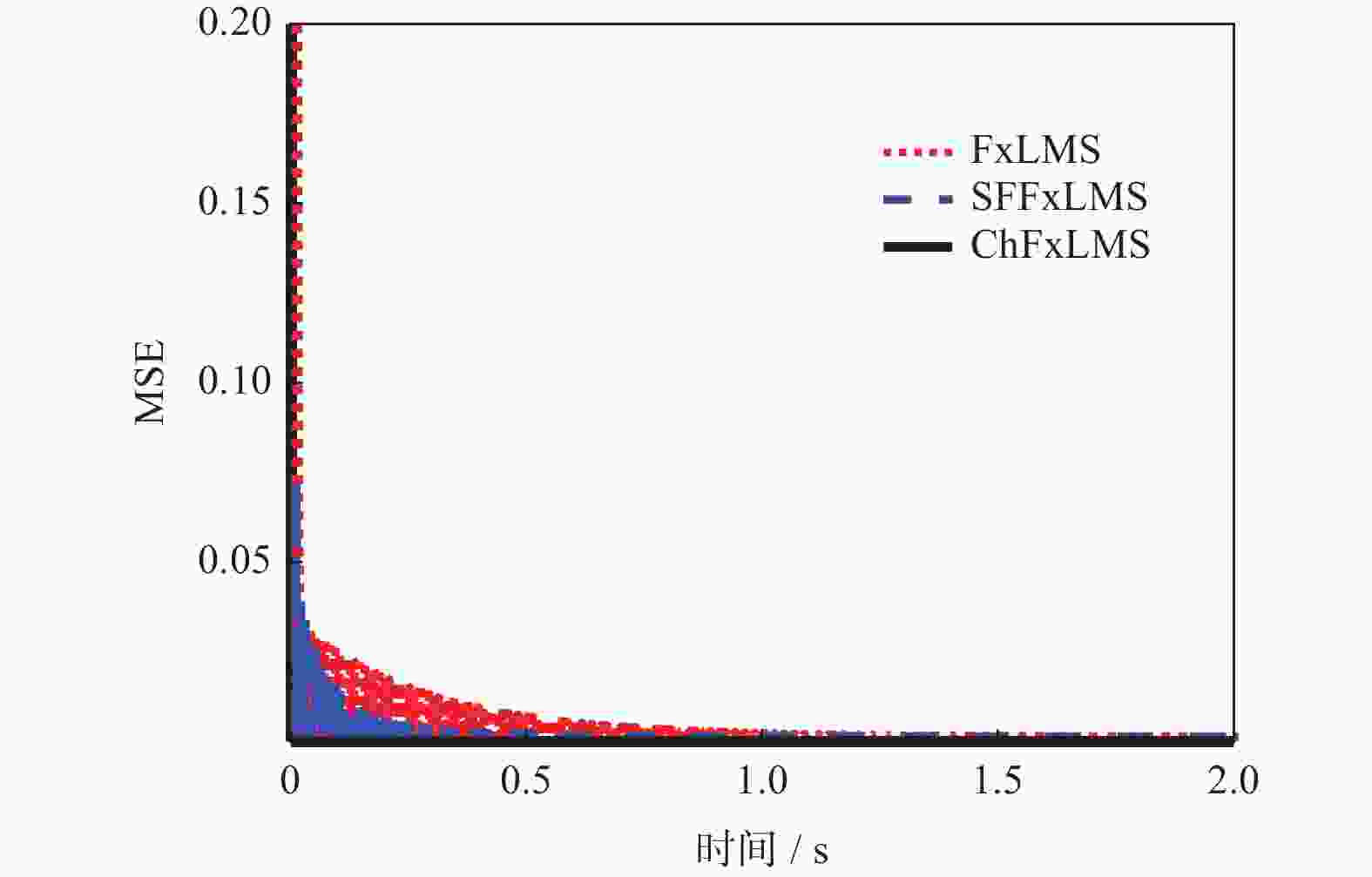
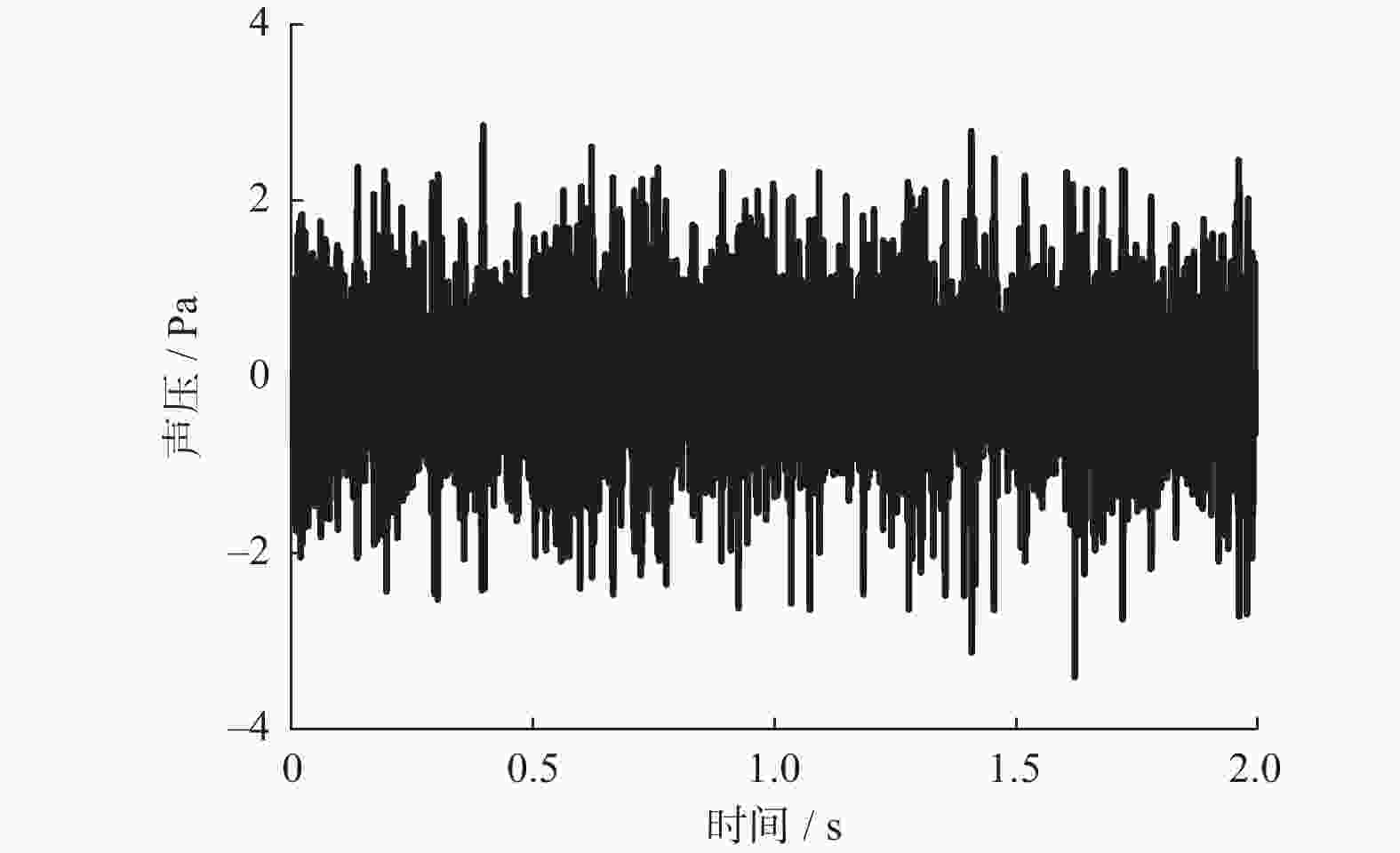
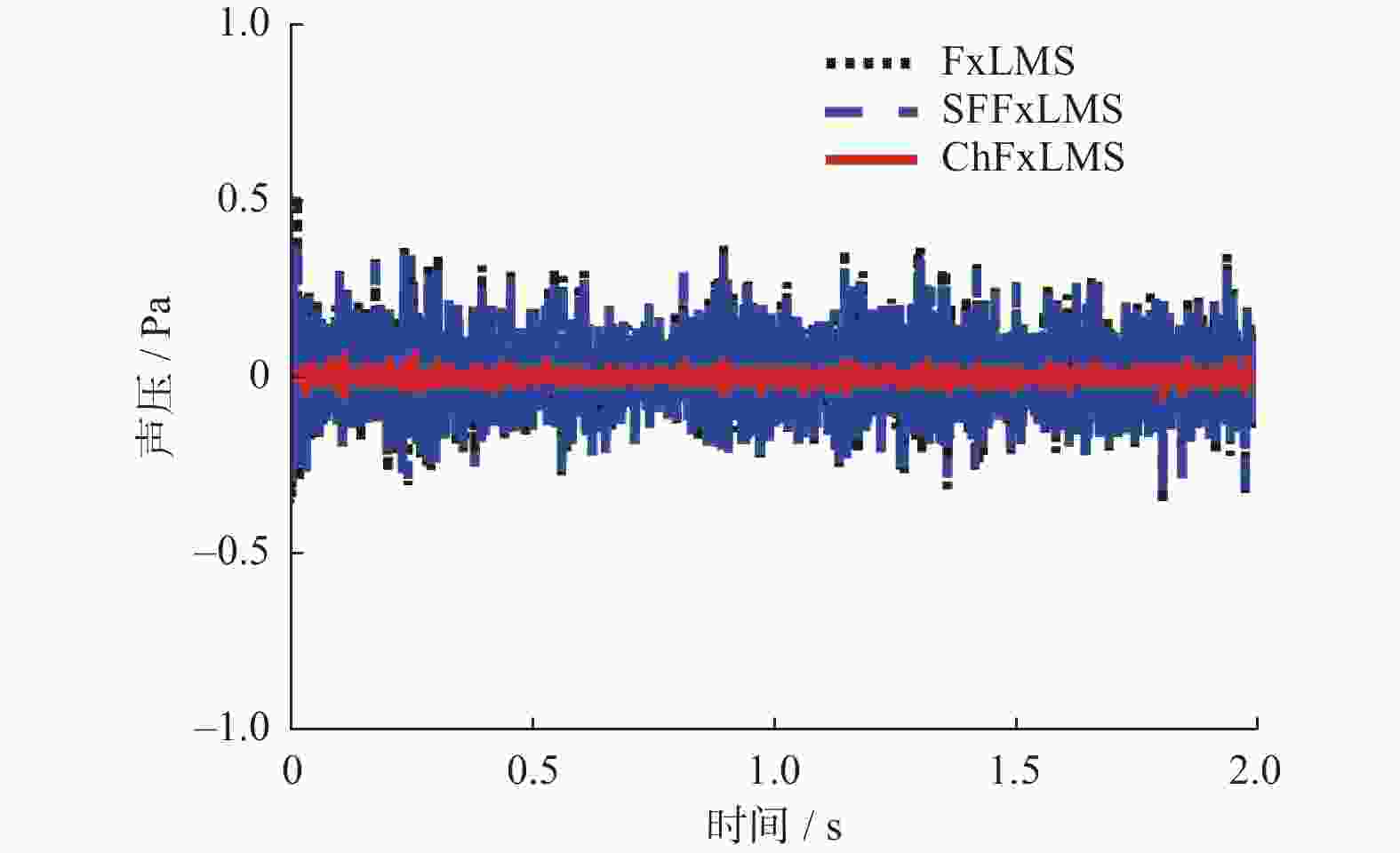
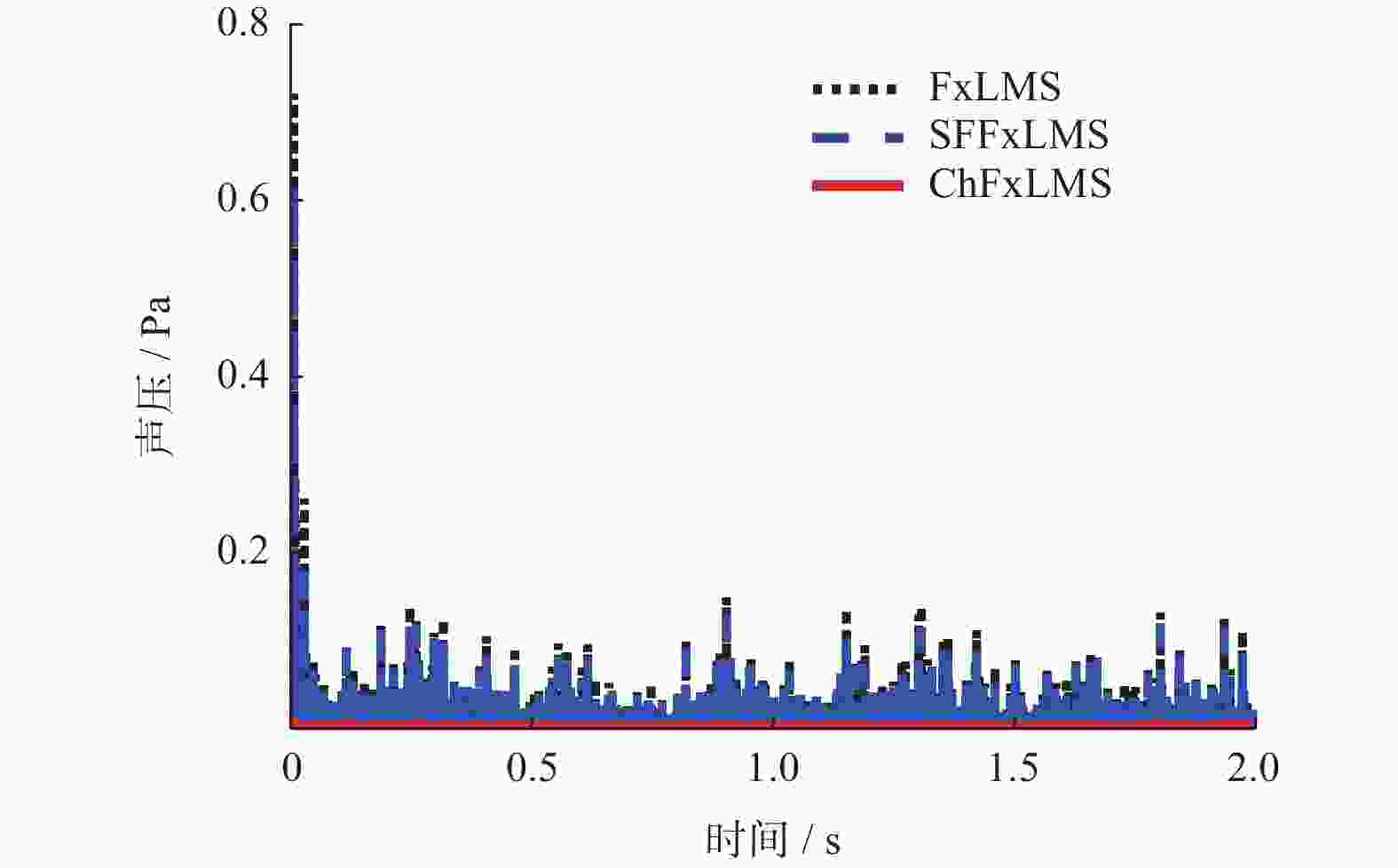
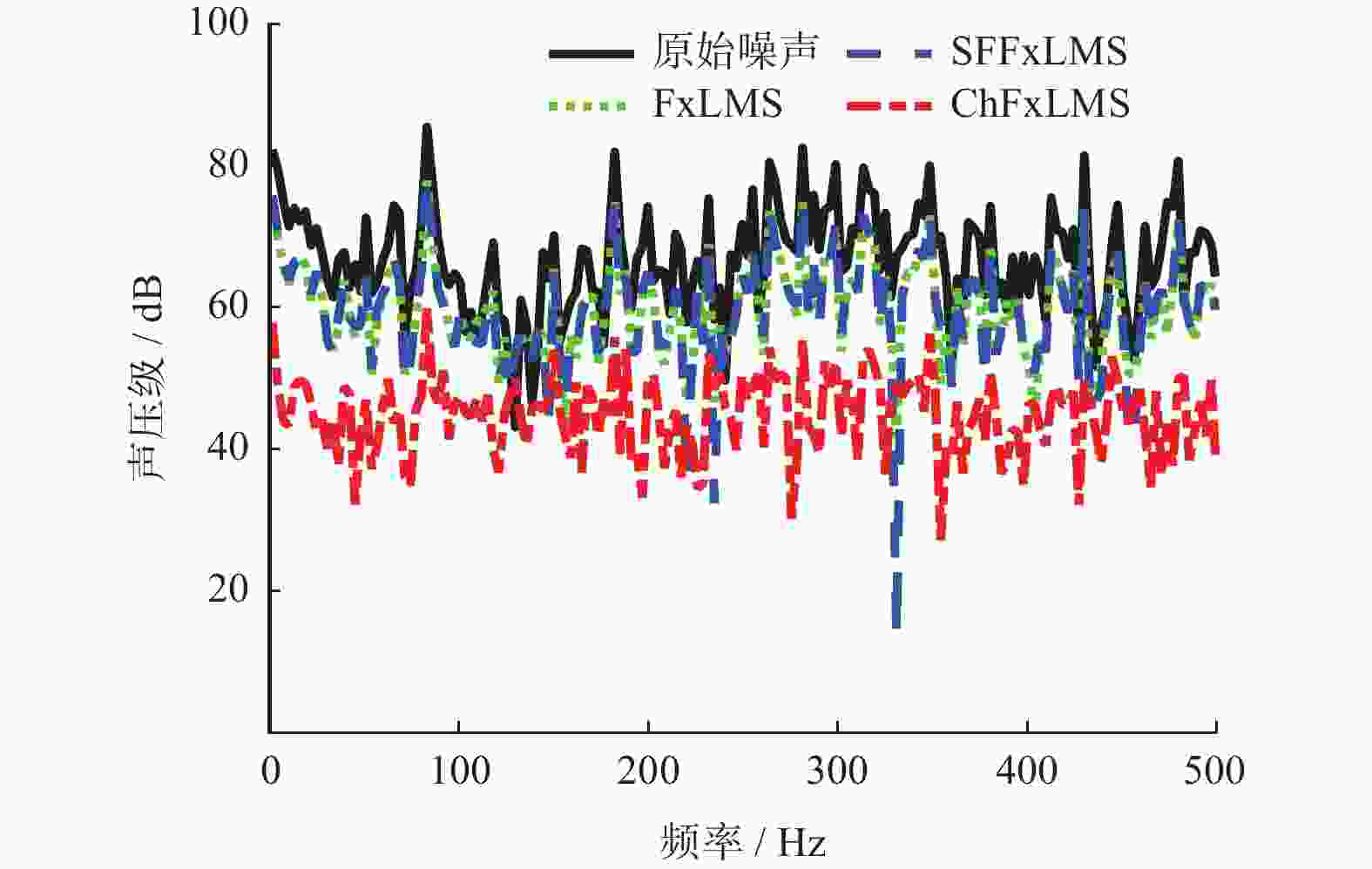
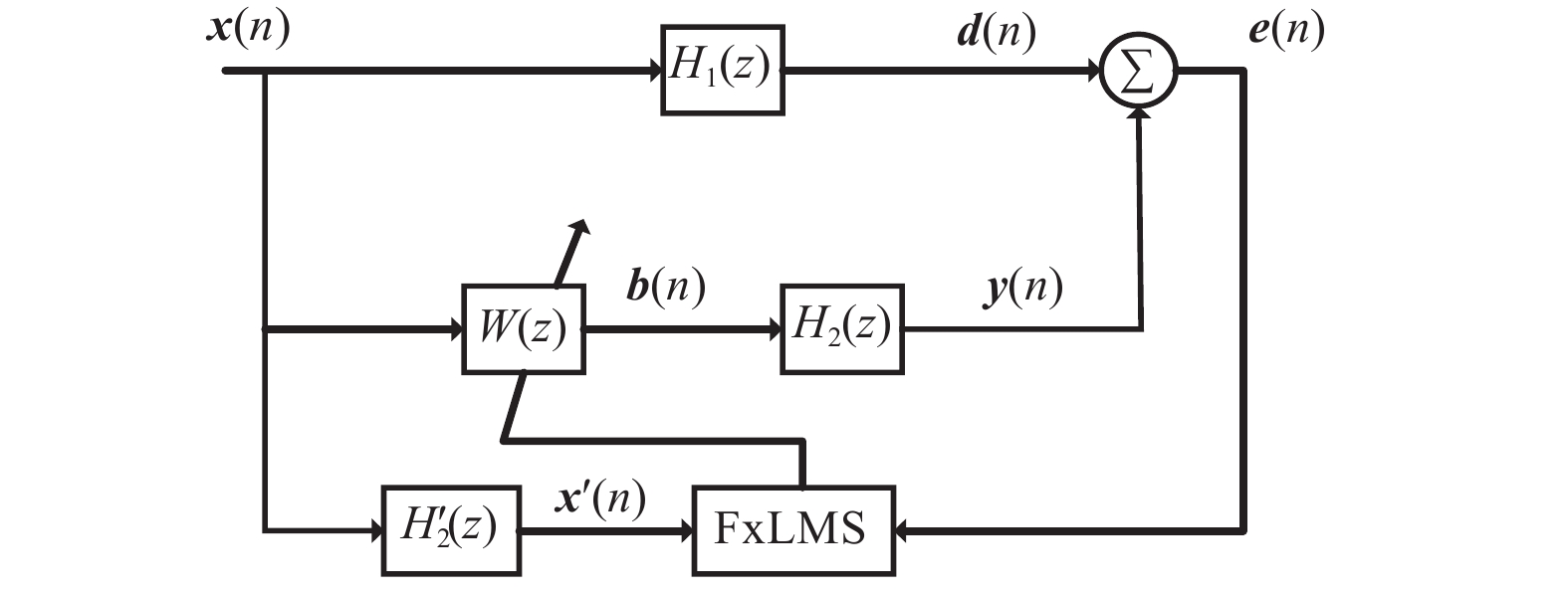
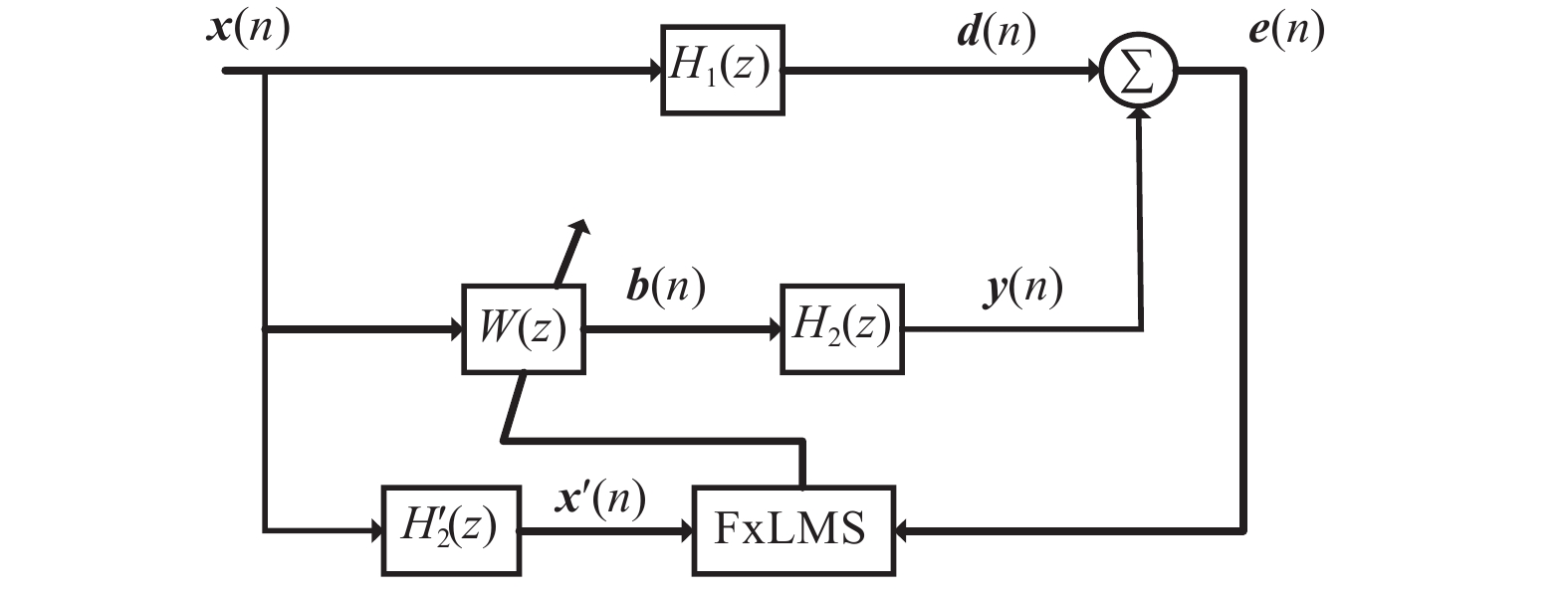
为改善滤波x最小均方（Filter-x Least Mean Square，FxLMS）算法不能同时兼顾稳态误差与收敛速度的不足，提出一种基于cosh函数的变步长FxLMS（Cosh-FxLMS，ChFxLMS）算法. 通过cosh函数建立误差信号与步长因子间的联系，使得步长因子按照cosh函数特性实时调整；分析不同参数对ChFxLMS算法性能的影响，为算法参数选取作指导；分别将正弦信号和实测织机信号作为输入信号，对ChFxLMS算法性能进行验证，并与FxLMS算法、基于sigmoid函数的变步长FxLMS（Sigmoid-FxLMS，SFFxLMS）算法进行对比. 仿真结果表明，ChFxLMS算法性能在时域和频域上都取得较好的控制效果. 分析结果表明，该算法能较大地降低稳态误差和提高收敛速度. 该研究成果可为工作空间噪声主动控制提供一种新思路.
Abstract:To improve the deficiency that the traditional filter-x least mean square (FxLMS) algorithm can not take into account the steady-state error and convergence speed, a variable step size FxLMS (Cosh-FxLMS, ChFxLMS) algorithm based on cosh function was proposed. The relationship between the error signal and the step factor was established by using the cosh function, so that step factor could adjust continuously according to the characteristics of the cosh function. The influence of different parameters on the performance of ChFxLMS algorithm was analyzed to provide guidance for the selection of algorithm parameters. And the sinusoidal signal and measured loom signal were used as input signals to verify the performance of ChFxLMS algorithm. It was compared with FxLMS algorithm and variable step size FxLMS algorithm based on sigmoid function (Sigmoid-FXLMS, SFFxLMS algorithm). The simulation results show that the performance of ChFxLMS algorithm has achieved good control results in time domain and frequency domain. Through comparative analysis, the algorithm can greatly reduce the steady-state error and improve the convergence speed. The research results will provide a new idea for active noise control in workspace.
-
Key words:
- active noise control /
- ChFxLMS algorithm /
- steady-state error /
- convergence speed
-
图 6 正弦信号输入时3种算法误差曲线图
Figure 6. Error curves of three algorithms when sinusoidal signal is input
图 7 正弦信号输入时3种算法均方误差曲线图
Figure 7. Mean square error curves of three algorithms when sinusoidal signal is input
图 10 织机噪声控制3种算法均方误差曲线图
Figure 10. Mean square error curves of three algorithms when loom noise is input
表 1 正弦信号输入时各算法参数值
Table 1. Parameter values of each algorithm when sinusoidal signal is input
参数 SFFxLMS算法 ChFxLMS算法 $ {\alpha _1} $ $ {\beta _1} $ $ {m_1} $ $ \alpha $ $ \beta $ $ m $ 值 4 6 1 40 10 1 
下载: 导出CSV
表 2 织机噪声控制时各算法参数值
Table 2. Parameter values of each algorithm when loom noise is input
参数 SFFxLMS算法 ChFxLMS算法 $ {\alpha _1} $ $ {\beta _1} $ $ {m_1} $ $ \alpha $ $ \beta $ $ m $ 值 4 0.9 1 20 5 1
下载: 导出CSV
-
[1] 胡异丁, 王凤森, 杨敏, 等. 一种改进变步长LMS自适应滤波算法[J] . 计算机仿真,2020,37(7):291 − 295. doi: 10.3969/j.issn.1006-9348.2020.07.057 [2] 韩啸, 陈钟荣. 一种改进反正切函数的变步长LMS算法[J] . 中国科技论文,2019,14(7):759 − 764,772. doi: 10.3969/j.issn.2095-2783.2019.07.010 [3] 吴瑶, 张海霞. 一种变步长LMS自适应滤波的改进算法[J] . 通信技术,2021,54(2):307 − 311. [4] 洪丹枫, 苗俊, 苏健, 等. 一种变步长凸组合LMS自适应滤波算法改进及分析[J] . 电子学报,2014,42(11):2225 − 2230. doi: 10.3969/j.issn.0372-2112.2014.11.015 [5] 陆森林, 默超. 车内ANC系统次级通道辨识及仿真研究[J] . 重庆理工大学学报(自然科学),2016,30(3):22 − 27. [6] GUO H, WANG Y S, LIU N N, et al. Active interior noise control for rail vehicle using a variable step-size median-LMS algorithm[J] . Mechanical Systems and Signal Processing,2018,109:15 − 26. doi: 10.1016/j.ymssp.2018.02.040 [7] 束建华, 付志浩. 改进FxLMS算法在主动振动控制中的应用[J] . 计算机工程与应用,2015,51(12):230 − 234. doi: 10.3778/j.issn.1002-8331.1411-0325 [8] 张帅, 王岩松, 张心光. 汽车车内噪声主动控制变步长NFB−LMS算法[J] . 声学技术,2019,38(6):680 − 685. [9] HUANG B Y, XIAO Y G, SUN J W, et al. A variable step-size FXLMS algorithm for narrowband active noise control[J] . Speech & language processing,2013,21(2):301 − 312. [10] MENG H, CHEN S M. A modified adaptive weight-constrained FxLMS algorithm for feedforward active noise control systems[J] . Applied Acoustics,2020,164:1 − 8. [11] 褚轶景, 麦卓明, 蔡陈之, 等. 一种新型基于分布式FxLMS的主动噪声控制算法与空间平滑[J] . 南京大学学报(自然科学),2021,54(4):683 − 688. [12] ZHU W Z, LUO L, XIE A T, et al. A novel FELMS-based narrowband active noise control system and its convergence analysis[J] . Applied Acoustics,2019,156:229 − 245. doi: 10.1016/j.apacoust.2019.07.003 [13] 徐洋, 张晓蕾, 盛晓伟, 等. 基于MEEMD−AIC的簇绒地毯织机噪声源识别方法[J] . 振动、测试与诊断,2018,38(6):1176 − 1181,1292. -
下载:
点击查看大图
计量
- 文章访问数: 278
- HTML全文浏览量: 114
- PDF下载量: 38
- 被引次数: 0
