Residual stress prediction based on equal thickness undeformed cutting thickness
-
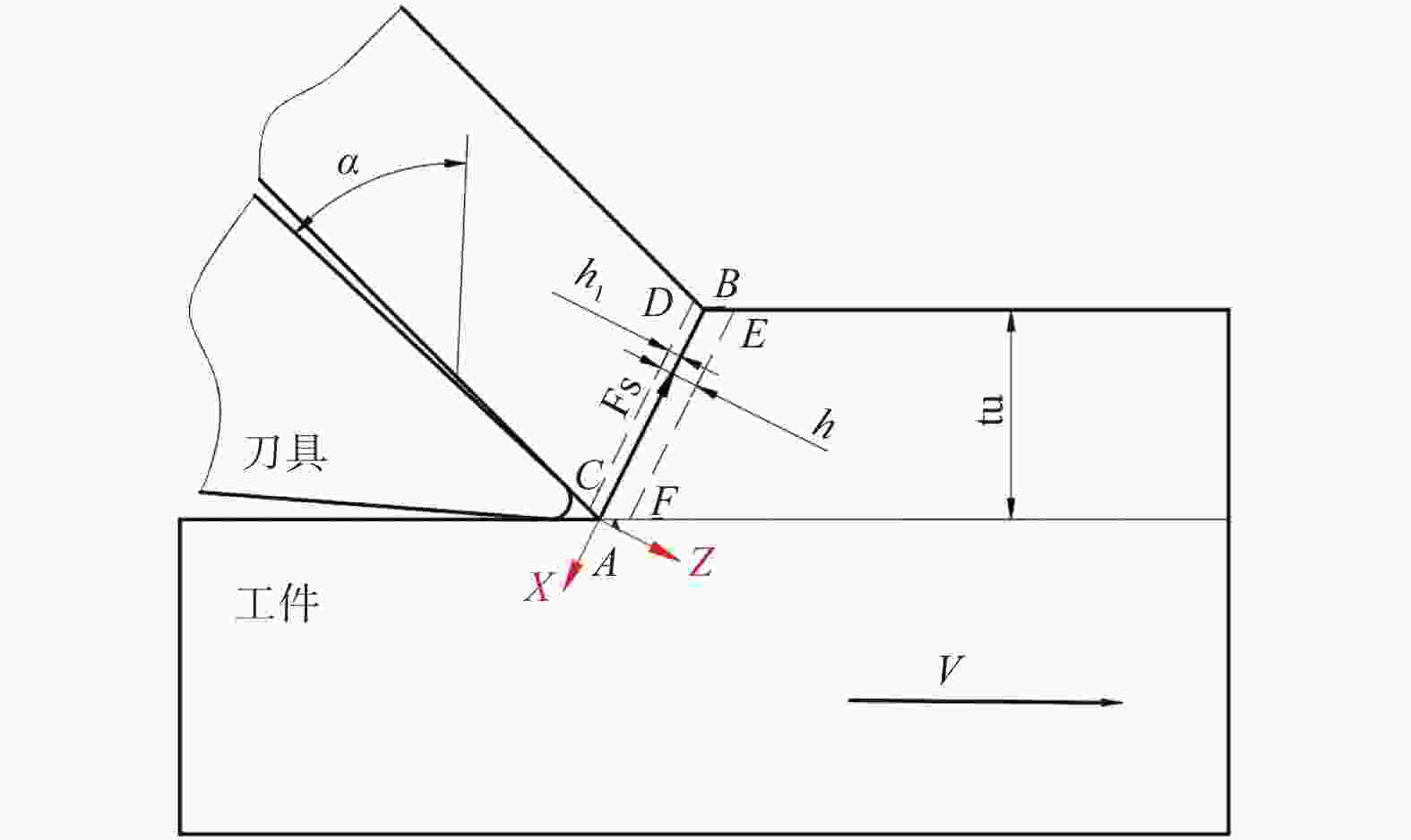
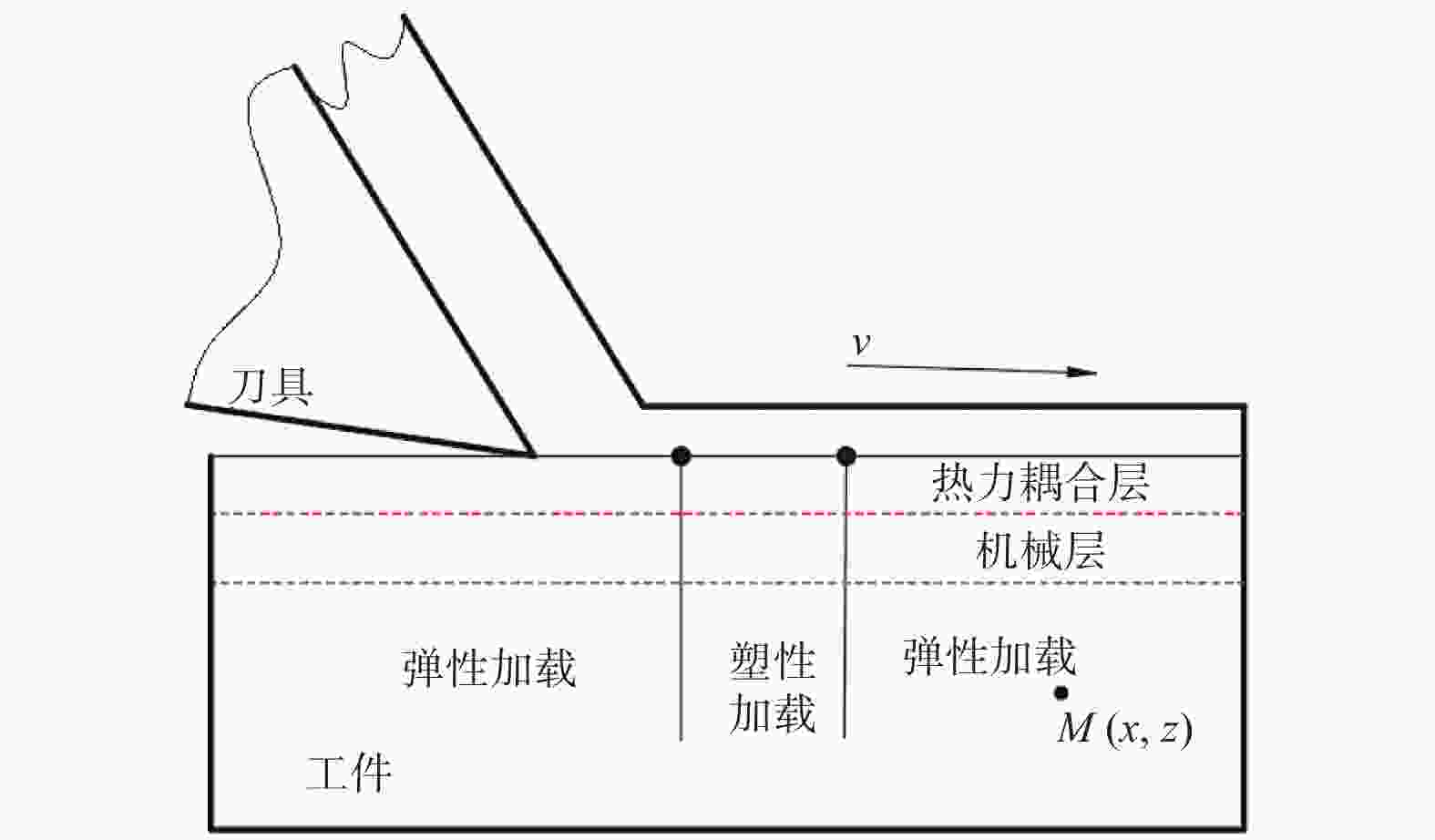
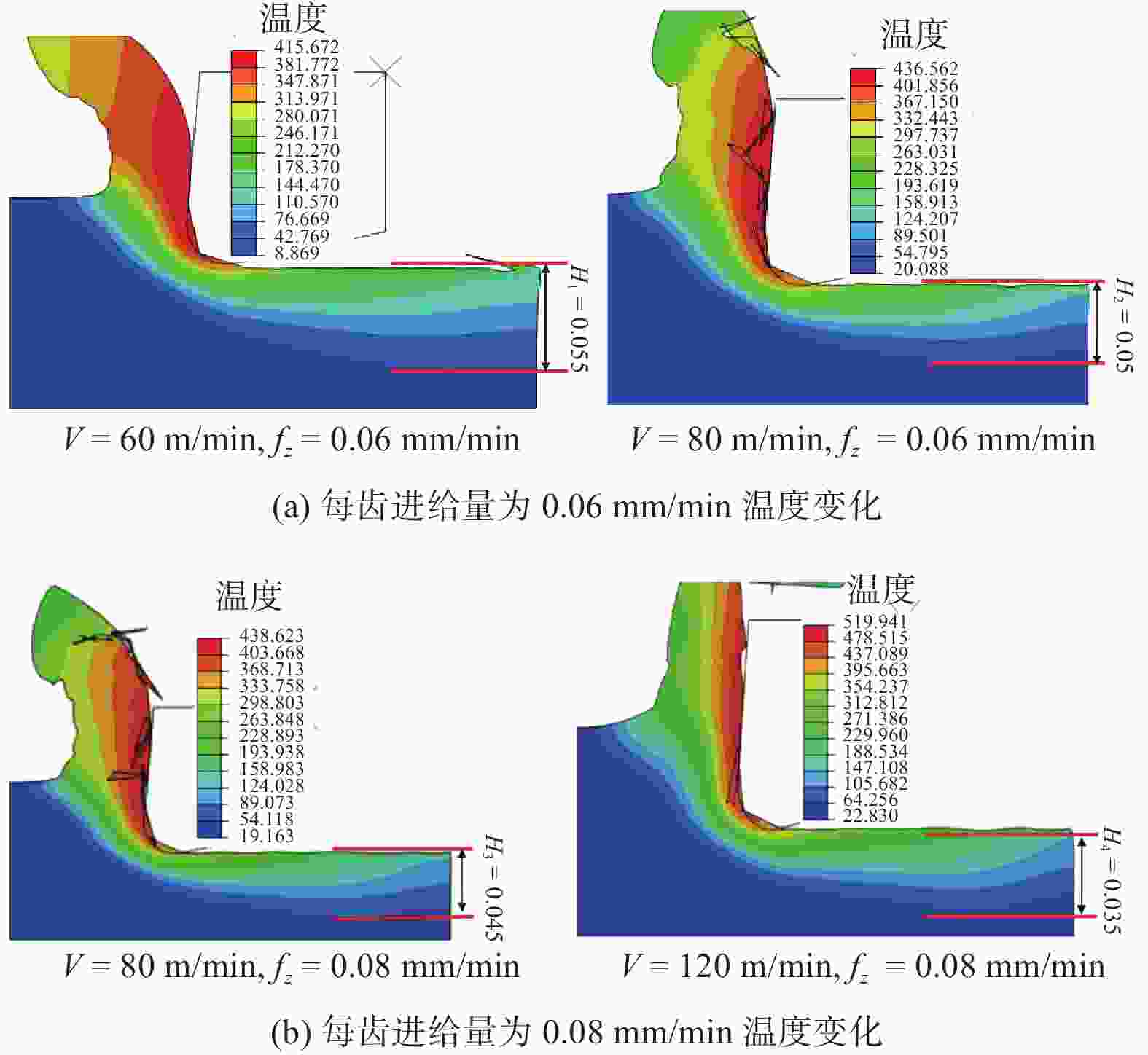
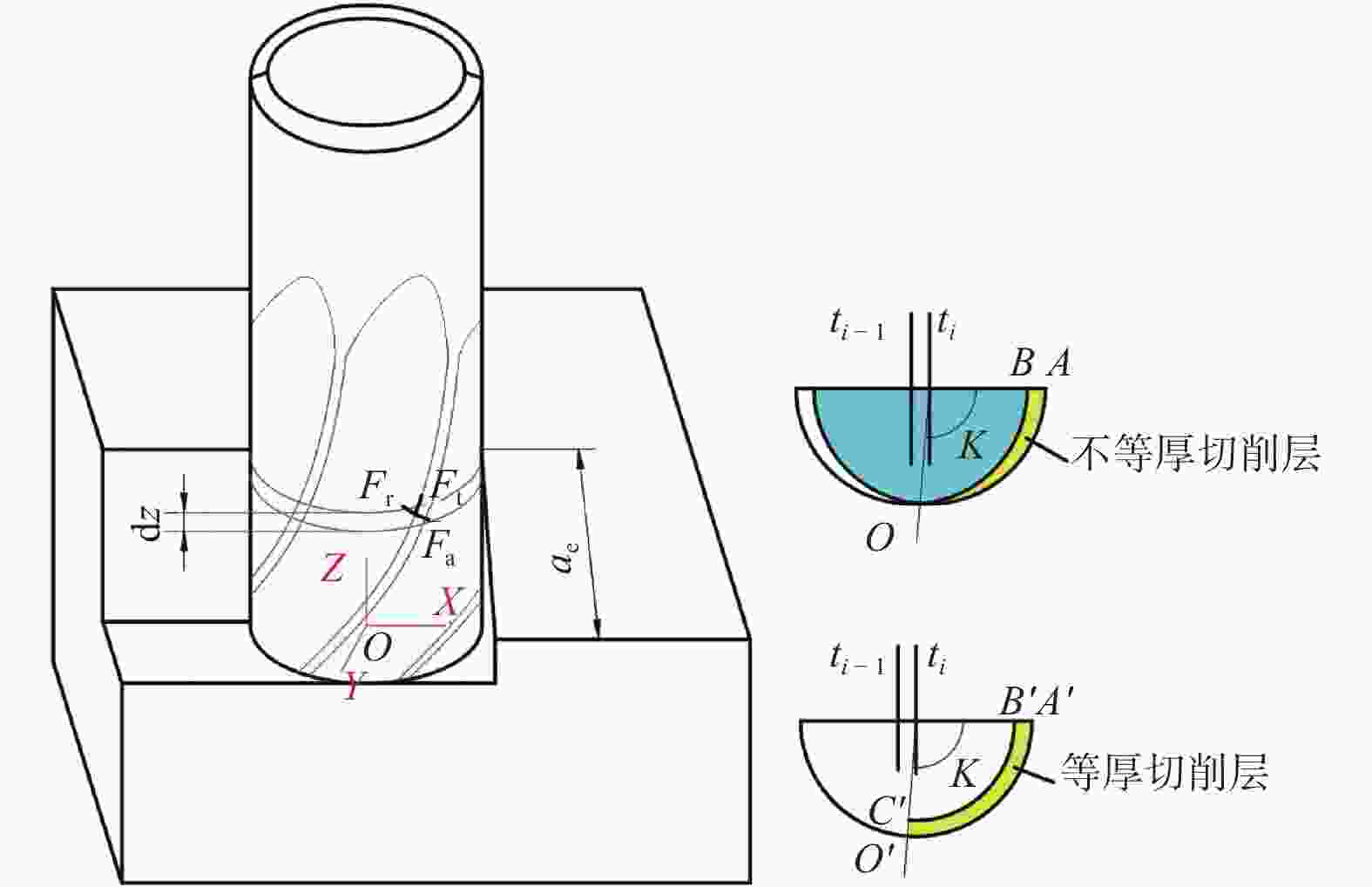
摘要: 机械加工引起的残余应力一直是制造领域关注的重点，表面残余应力状态能反映零部件性能与使用寿命. 为更好地了解铣削加工零件表面与次表面残余应力状态，将铣削不等厚未变形切削厚度转换为等厚未变形切削厚度进行微元铣削力建模. 通过仿真建立2D等厚未变形切削厚度模型研究切削钛合金时的温度，结合微元力与温度模型对铣削后加工表面残余应力进行预测，并将残余应力预测值、仿真值与实测值进行比较. 结果表明，残余应力仿真值与实测值的变化趋势基本一致，通过等厚未变形切削厚度建立的残余应力预测模型能够反映表面应力状态.Abstract: Residual stress caused by machining has always been the focus of manufacturing field. The surface residual stress state can reflect component performance and service life. In order to better understand surface and subsurface residual stress state of milled parts, the milled undeformed cutting thickness of unequal thickness was converted into the undeformed cutting thickness of equal thickness for micro milling force modeling. A 2D equal thickness undeformed cutting thickness model established by simulation was used to study the temperature when cutting titanium alloy, the surface residual stress after milling was predicted by combining the microelement force and temperature model, and predicted value, simulated value and measured value of residual stress were compared. The results show that the variation trend of simulated value and measured value of residual stress is basically the same, and the proposed residual stress prediction model established by equal thickness undeformed cutting thickness can reflect the surface stress state.
-
图 2 等效平面与法平面内不等厚二维正交切削
Figure 2. Two dimensional orthogonal cutting of unequal thickness in equivalent plane and normal plane
表 1 TC4本构参数表
Table 1. TC4 J−C model parameters
A/MPa B/MPa C m n Tm/℃ Tr/℃ 862.5 331.2 0.012 0.8 0.34 1580 20 
下载: 导出CSV
表 2 TC4热导率和比热容
Table 2. TC4 thermal conductivity and specific heat capacity
物理性能 20 ℃ 100 ℃ 200 ℃ 300 ℃ 400 ℃ 500 ℃ 热导率/(W•(m•℃)−1) 6.8 7.4 8.7 9.8 10.3 11.8 比热容/(J•(kg•℃)−1) 611 624 653 674 691 703
下载: 导出CSV
表 4 试验参数表
Table 4. Experimental parameters
序号 铣削速度/
(m•min−1)每齿进给/
(mm•min−1)铣削深度/
mm铣削宽度/
mm1 60 0.06 7 0.5 2 80 0.06 3 80 0.08 4 90 0.08 5 100 0.08 6 110 0.08
下载: 导出CSV
-
[1] 季霞. 微量润滑切削表面残余应力预测建模[D]. 上海: 上海交通大学, 2014. [2] CARL E J. A mathematical model for the estimate ion of the effects of residual stresses in aluminum plates[D]. Saint Louis: Washington University, 2005. [3] WAN M, YE X Y, YANG Y, et al. Theoretical prediction of machining-induced residual stresses in three-dimensional oblique milling processes[J] . International Journal of Mechanical Sciences,2017,133:426 − 437. [4] LIU C R, BARASH M M. Variables governing patterns of mechanical residual stress in a machined surface[J] . Journal of Engineering for Industry,1982,104(3):257 − 264. [5] YOUNG K A. Machining-induced residual stress and distortion of thin parts[D]. Saint Louis: Washington University, 2005. [6] CAPELLO E. Residual stresses in turning Part I: Influence of process parameters[J] . Journal of Materials Processing Technology,2005,160(2):221 − 228. doi: 10.1016/j.jmatprotec.2004.06.012 [7] LIU M, TAKAGI J, TSUKUDA A. Effect of tool nose radius and tool wear on residual stress distribution in hard turning of bearing steel[J] . Journal of Materials Processing Technology,2004,150(3):234 − 241. doi: 10.1016/j.jmatprotec.2004.02.038 [8] 张峥. 飞机弱刚性铝合金结构件的残余应力和加工变形控制研究[D]. 南京: 南京航空航天大学, 2016. [9] ZHU S S, LIU J, DENG X. Modification of strain rate strengthening coefficient for Johnson-Cook constitutive model of Ti6Al4V alloy[J] . Materials Today Communications,2021,26:102016. [10] WU H B, TO S. Serrated chip formation and their adiabatic analysis by using the constitutive model of titanium alloy in high speed cutting[J] . Journal of Alloys and Compounds,2015,629:368 − 373. doi: 10.1016/j.jallcom.2014.12.230 [11] WAN M, YE X Y, WEN D Y, et al. Modeling of machining-induced residual stresses[J] . Journal of Materials Science,2019,54(1):1 − 35. [12] HUANG X D, ZHANG X M, DING H. An analytical of residual stress for flank milling of Ti-6Al-4V[J] . Procedia CIRP,2015,31:287 − 292. doi: 10.1016/j.procir.2015.03.061 [13] ZHANG W Q, WANG X L, HU Y J, et al. Predictive modelling of microstructure changes, micro-hardness and residual stress in machining of 304 austenitic stainless steel[J] . International Journal of Machine Tools & Manufacture: Design, Research and Application,2018,130-131:36 − 48. [14] PAN Z, SHIH D S, GARMESTANI H, et al. Residual stress prediction for turning of Ti-6Al-4V considering the microstructure evolution[J] . Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture,2019,233(1):109 − 117. [15] JI X, KANG Z, ZHANG X P. A new methodology to validate the cutting temperature theoretical model in super-finish hard machining[J] . Avanced Science Letters,2011,4(4/5):1561 − 1565. [16] LIANG S Y, SU J C. Residual stress modeling in orthogonal machining[J] . CIRP Annals Manfacturing Technology,2007,56(1):65 − 68. doi: 10.1016/j.cirp.2007.05.018 [17] 周瑞虎. 复杂曲面铣削加工表面残余应力预测与实验研究[D]. 武汉: 华中科技大学, 2019. [18] LIANG X, LIU Z, WANG B, et al. Prediction of residual stress with multi-physics model for ortho-gonal cutting Ti-6Al-4V under various tool wear morphologies[J] . Journal of Materials Processing Technology,2021,288:116908. doi: 10.1016/j.jmatprotec.2020.116908 [19] RAHUL Y, VIPINDAS K, MATHEW J. Methodology for prediction of sub-surface residual stress in micro end milling of Ti-6Al-4V alloy[J] . Journal of Manufacturing Processes,2021,62:600 − 612. doi: 10.1016/j.jmapro.2020.12.031 [20] ÖZEL T, ALTAN T. Process simulation using finite element method: Prediction of cutting forces, tool stresses and temperatures in high-speed flat end milling[J] . International Journal of Machine Tools and Manufacture,2000,40(5):713 − 738. [21] LI B L, HU Y J, WANG X L, et al. An analytical model of oblique cutting with application to end milling[J] . Machining Science and Technology,2011,15(4):453 − 484. [22] WALDORF D J, DEVOR R E, KAPOOR S G. A slip-line field for ploughing during orthogonal cutting[J] . Journal of Manufacturing Science & Engineering,1998,120(4):693 − 699. [23] 易俊杰. 钛合金高速铣削力试验与有限元数值分析[D]. 南京: 南京航空航天大学, 2009. -
下载:
点击查看大图
图(8) / 表(4)
计量
- 文章访问数: 245
- HTML全文浏览量: 124
- PDF下载量: 39
- 被引次数: 0
