Transient analysis of misaligned journal bearings based on fluid-structure interaction approach
-
摘要:
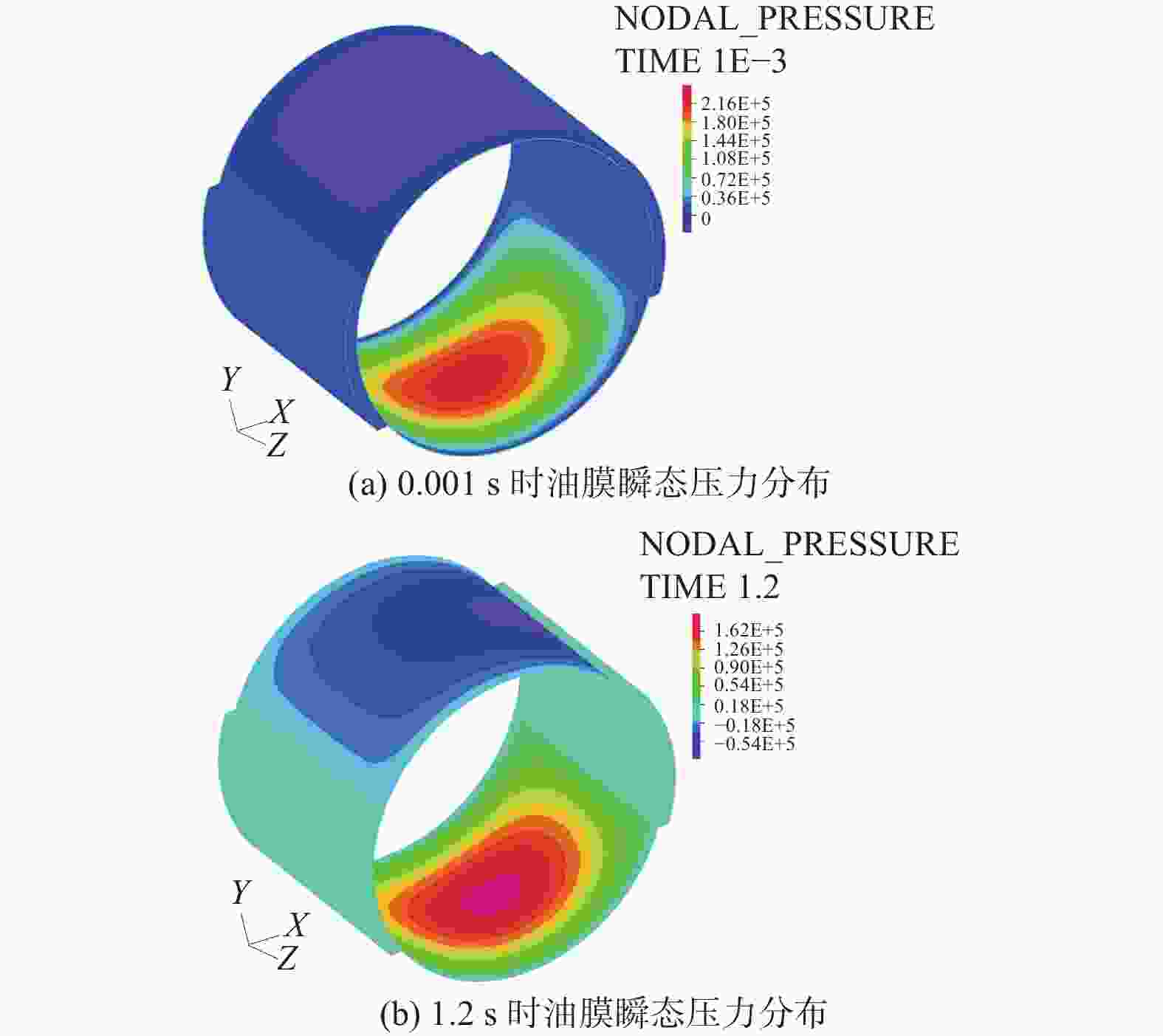
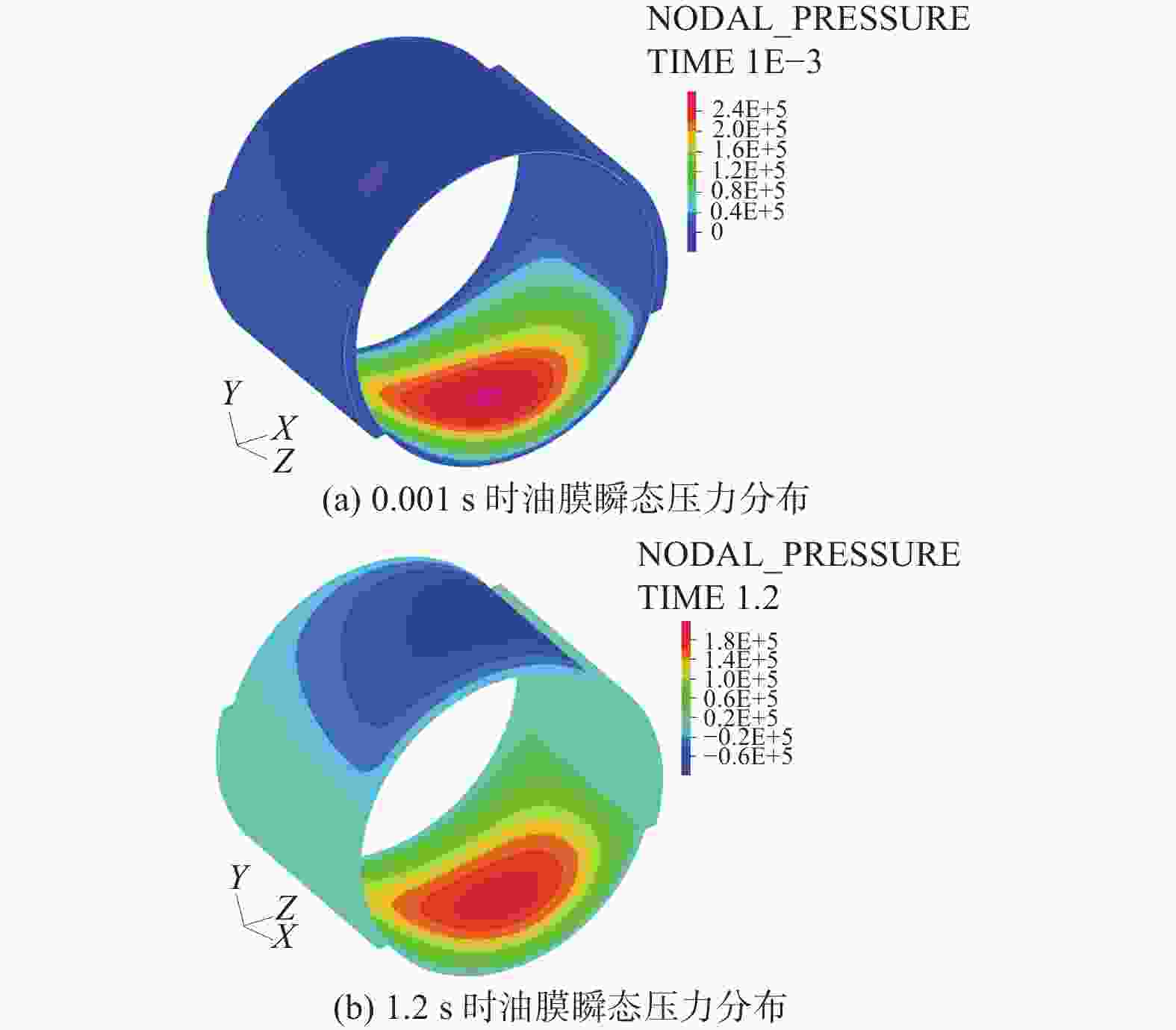
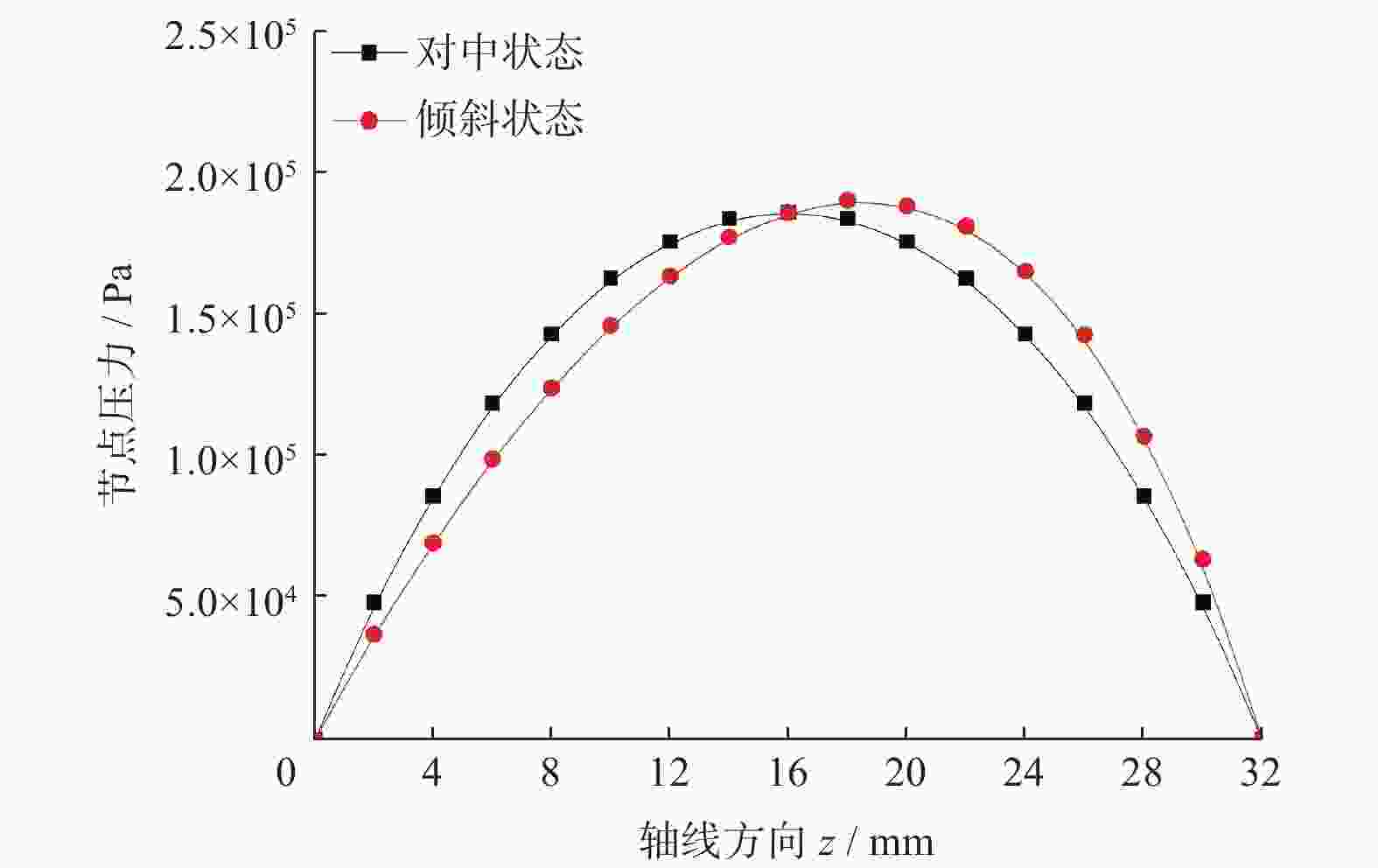
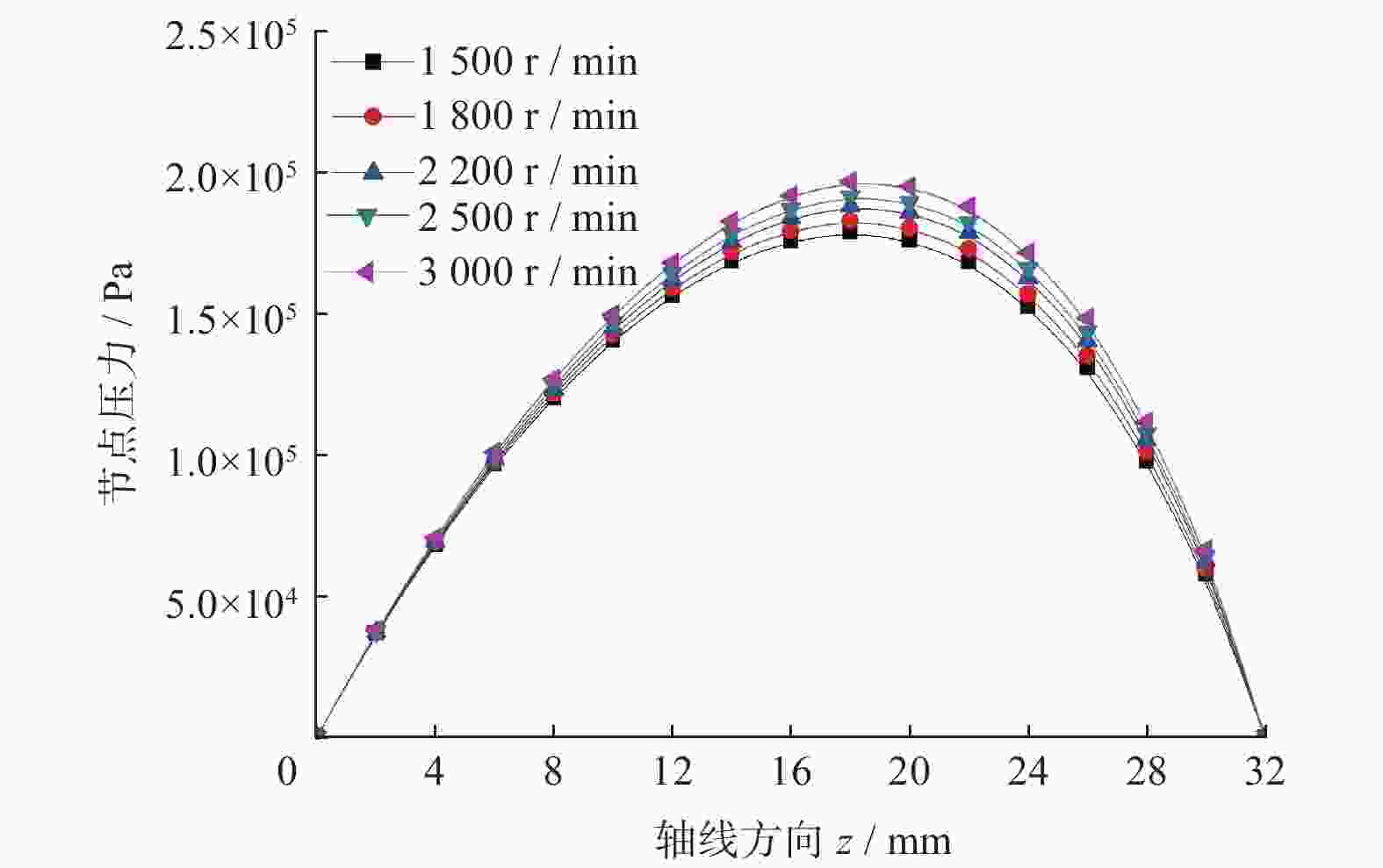
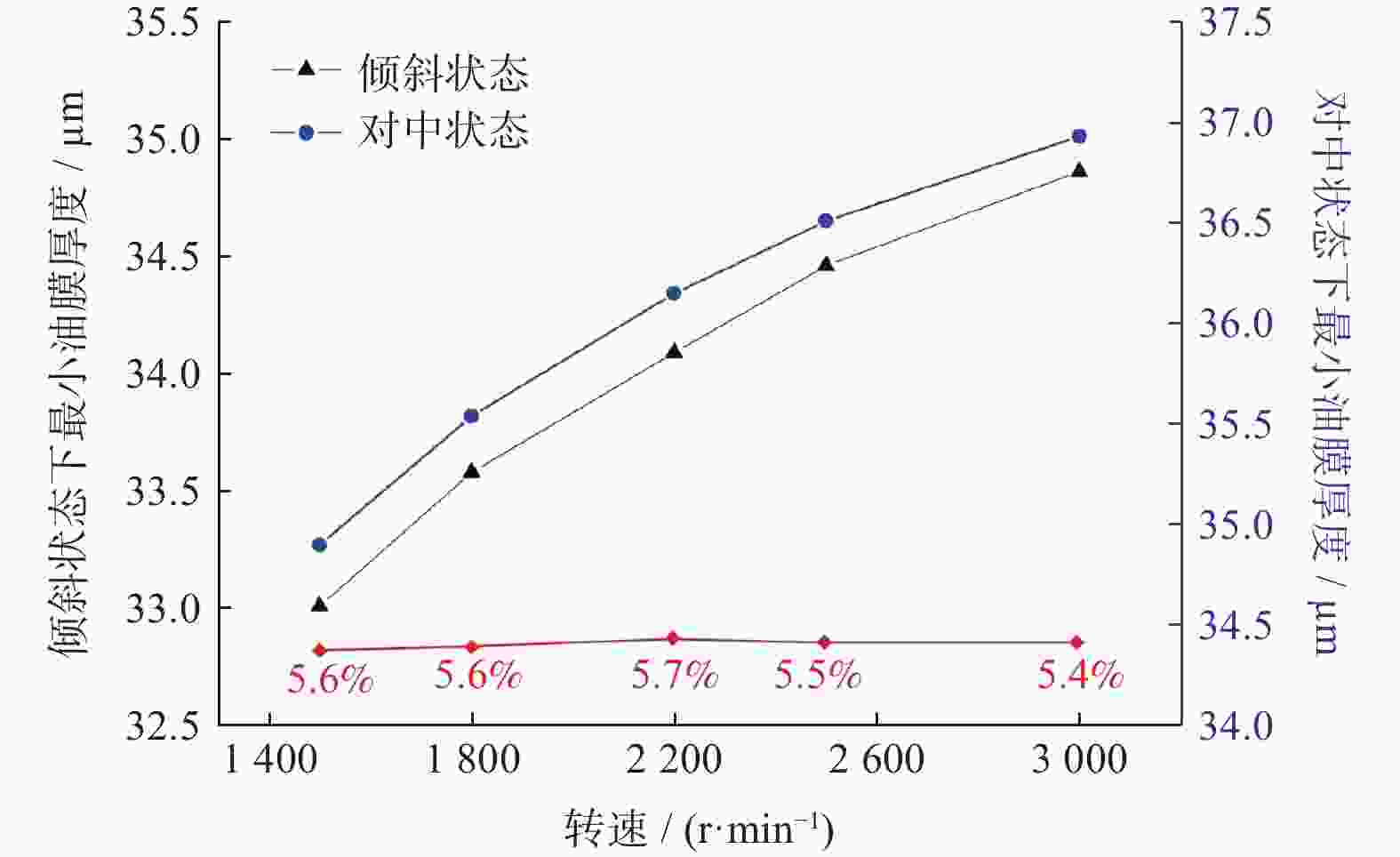
考虑轴受力产生变形引起的轴倾斜，采用流固耦合方法，直接求解Navier−Stokes方程，对滑动轴承系统中轴和润滑油膜进行三维瞬态分析，同时求解流场和固体域，得到油膜动态压力分布、轴心的运动轨迹和不同转速下油膜厚度分布. 结果表明，轴倾斜使油膜压力分布和轴心轨迹变化明显，最小油膜厚度减小，流场压力峰值增大. 通过对滑动轴承的三维瞬态分析可以预测轴承工作过程中实时的轴心轨迹、压力分布、油膜厚度等润滑特性，为滑动轴承的优化设计提供参考.
Abstract:The shaft is deformed with the action of load. The misalignment due to deformation caused by the action of load is considered. The fluid-structure interaction method was used. Navier-Stokes equation was solved directly. The three-dimensional transient analysis of shaft and oil film in journal bearing system was carried out. The flow field and solid domain were solved at the same time. Transient film pressure distribution, trajectory of journal center and minimum oil film thickness under different rotate speeds were solved. The results show that the oil film pressure distribution and thickness of oil film change obviously. The minimum oil film thickness decreases, the peak oil film pressure increased when misalignment was considered. The real-time trajectory of journal center, oil film thickness and transient film pressure distribution can be predicted by the transient analysis, which is very significant for the optimal design of journal bearing.
-
Key words:
- journal bearing /
- misalignment /
- transient analysis /
- oil film thickness
-
滑动轴承在高速和高精度机械设备中应用广泛，其可靠性直接影响到设备的精度和使用寿命，滑动轴承的润滑分析一般是以轴颈轴线与轴承孔轴线平行（轴承与轴颈对中状态）为前提进行研究的，但在实际工作过程中，轴在载荷作用下会产生变形，轴变形引起轴颈在轴承孔中倾斜. Mukherjee等[1]通过对油膜厚度表达式进行修正，得到倾斜有限长滑动轴承油膜压力和油膜厚度模型；孙丽军等[2]认为重载轴承在轴颈倾斜角较大时，可能导致轴颈与轴承碰磨甚至烧瓦；Zhu等[3]考虑热效应，求解湍流雷诺润滑方程和能量方程，计算轴倾斜时轴承轴颈表面粗糙度对轴颈轴承的润滑性能的影响；王亚兵等[4]研究轴倾斜时水润滑橡胶艉轴承的静态特性，得到倾斜角对油膜力矩和最小油膜厚度的影响规律；Sun等[5]用有限差分法求解雷诺方程，分析轴倾斜时不同轴颈倾斜度和偏心率时的润滑特性；Lyu等[6-7]研究轴倾斜时混合润滑的滑动轴承，计算表明轴倾斜会导致轴承名义液膜厚度降低，从而增大混合润滑状态下的摩擦因数. 刘洋洋等[8]采用差分求解方法求解轴倾斜下水润滑橡胶径向轴承动力学问题，分析偏心率和倾斜角的变化对轴承动特性系数的影响，发现刚度和阻尼系数随偏心率的增大而增大. 可见，滑动轴承中轴倾斜对润滑特性的影响不可忽略. 以上研究主要采用雷诺方程进行稳态分析，应用雷诺方程求解时存在一些假设，与实际存在一定的偏差. Gertzos等[9-13]直接以Navier-Stokes方程为基础研究轴承润滑特性，没有考虑轴倾斜因素；朱希玲等[14]计算时没有考虑轴倾斜对润滑特性的影响. 本研究以某滑动轴承试验台[15]为例，对该滑动轴承进行瞬态分析，求解动态油膜力和动态油膜刚度.
1. 数学模型
1.1 流体控制方程
流体的基本理论方程是质量守恒方程[11]为
∂ρ∂t+∇•(ρv)=0 (1) 式中：t为时间；
$ \rho $ 为流体密度；${\boldsymbol{v}}$ 为速度矢量. 动量守恒方程是Navier−Stokes方程为∂∂t(ρv)+∇•(ρvv)=−∇p+∇•(ˉˉτ)+ρg+F (2) 式中：
$ p $ 为压力；$\bar{\bar \tau }$ 为应力张量；$\rho {\boldsymbol{v}}$ 和${\boldsymbol{F}}$ 分别为流体部分的体力矢量和外力矢量.ˉˉτ=μ[(∇v+∇vT)−2/3∇•vI] (3) 式中：μ为流体黏度；
$ I $ 为单位张量.1.2 固体控制方程
对固体施加位移扰动时，固体的控制方程可描述为
ρs¨ds=∇•σs+fs (4) 式中：
${\rho }_{{\rm{s}}}\mathrm{为}\mathrm{固}\mathrm{体}\mathrm{密}\mathrm{度}$ ；${\sigma }_{{\rm{s}}}\mathrm{为}\mathrm{固}\mathrm{体}\mathrm{柯}\mathrm{西}\mathrm{应}\mathrm{力}\mathrm{张}\mathrm{量}$ ；${{\boldsymbol{f}}}_{{\rm{s}}}$ 为外力体向量；${\ddot{d}}_{{\rm{s}}}$ 为固体区域的重力加速度.1.3 边界条件
油膜内表面与轴的外表面接触，定义为流体和固体的耦合面，在耦合面上施加切向速度，油膜外表面与轴瓦接触，定义为固定壁面，在流体与固体的耦合面上，流体与固体同时满足位移和力平衡的条件. 流体和固体的耦合方程采用直接法求解. 当计算机内存足够大时，采用直接法可以省去耦合面平衡方程求解时的磁盘读取和存储操作，求解速度快. 如果内存容量较小时，可以采用迭代法，分别求解流体和固体域. 当力与位移的相对残差小于0.01时，认为此迭代步收敛.
2. 数值计算
2.1 计算模型
根据文献[15]对润滑特性进行瞬态分析，结合流固耦合方法，计算油膜瞬态压力分布、轴心轨迹、最小油膜厚度等. 计算时考虑轴倾斜对润滑特性的影响，建立轴承轴向示意图如图1所示. 建模时只要保证P3点处轴与轴承不干涉.
建立轴和油膜的流固耦合模型，轴的弹性模量为2.1 × 1011 Pa，密度为7800 kg/m3，泊松比为0.33，轴直径为0.040 m. 润滑油的黏度为0.027 Pa•s，轴承所受的外载荷W为150 N，轴承长度L为0.032 m，两端轴承中心的距离S为0.732 m. 轴在轴承中的倾斜角计算公式为γ = (WS2)/(16EJ) [16]. 其中，W为外载荷；E为轴的弹性模量；J为轴截面惯性矩. 有限元模型参考文献[14]，采用扫掠网格划分技术划分网格，计算时假设流体不可压缩，等温，层流. 轴上施加载荷150 N，采用流固耦合分析，考虑流场和轴之间的相互作用，对流场和应力应变场同时进行求解.
2.2 轴心轨迹
轴转速为2500 r/min，轴颈在轴承中的位置由油膜力与作用在轴承上的负载之间的关系确定. 建模时轴颈在轴承中的初始位置只要保证P3点轴颈和轴承不干涉即可.
不考虑轴倾斜时，通常按轴承与轴颈对中状态开始计算，轴颈轴线上各点轴心轨迹相同. 初始时，轴颈在负载作用下向下移动，随着油膜厚度减小，油膜力逐渐增大，下半周油膜平均压力大于上半周油膜平均压力时，轴颈向上浮起，计算时通过流固耦合方法，同时求解流场和固体场，实时计算轴颈位置和油膜力大小，轴心轨迹如图2所示. 1.2 s后油膜力与载荷平衡.
倾斜状态时，建模时考虑轴变形，轴颈轴线与轴承轴线不重合，以图1中P1、P2、P3点为例，竖直方向上，P1与轴承孔轴线距离最小，P3与轴承孔轴线距离最大，油膜厚度较小. 初始时，P1、P2、P3点处由于轴倾斜，油膜厚度比对中状态小，油膜力较大，轴颈在油膜力的作用下，P1、P2、P3点处轴均向上浮起，1.3 s后油膜力与载荷平衡，由于轴倾斜，轴颈轴线上各点起始位置和平衡位置坐标不同. P1、P2、P3点的轴心轨迹如图3所示. 考虑轴变形引起的轴倾斜更能反映轴心实际运动情况，初始时油膜厚度较小，油膜力较大，轴向上运动至平衡位置. 根据轴心轨迹，可以确定各个时刻轴上各点对应的坐标值、各时刻油膜压力分布和最小油膜厚度等.
2.3 瞬态油膜压力分布
转速为2500 r/min，对中状态时，瞬态压力分布如图4所示，沿轴向对称分布，0.001 s时，在重力作用下，油膜厚度迅速减小，流场压力最大值为2.16 × 105 Pa. 1.2 s时，轴运动到平衡位置，流场压力最大值有所下降，为1.62 × 105 Pa.
倾斜状态时瞬态压力分布如图5所示. 压力分布沿轴线方向不对称，流场压力最大值靠近轴承端面（P3点所在右端面），此处油膜厚度较小. 0.001 s时，轴倾斜使油膜厚度变小，流场压力最大值为2.4 × 105 Pa, 轴运动到平衡位置，流场压力最大值有所下降，为1.8 × 105 Pa. 比同一时刻对中状态时数值大.
3. 结果分析
在平衡位置，转速为2500 r/min时，沿轴线方向流固耦合面上节点压力分布如图6所示，轴承沿轴线方向长度为32 mm. 对中状态时，节点压力对称分布，以油膜压力峰值位置为界，向两边逐渐减小；倾斜状态时，油膜厚度减小，沿轴向方向不对称，轴线方向上节点压力最大值明显增加，压力峰值位置向轴承端部偏移.
倾斜状态下，分别计算转速为1500、1800、2200、2500、3000 r/min时流场的压力分布，沿轴线方向流固耦合面上节点压力随转速变化的曲线如图7所示. 随转速增加，轴线方向上节点压力增大，压力峰值随转速增加而增大，压力峰值位置靠近轴承端面.
图 7 沿轴线方向节点压力随转速变化曲线Figure 7. Curve of nodal pressure along Z direction at different rotation speeds最小油膜厚度是滑动轴承系统中最重要的参数之一. 倾斜状态和对中状态下，分别计算转速为1500、1800、2200、2500、3000 r/min时的最小油膜厚度，不同转速下最小油膜厚度的变化曲线如图8所示. 转速增加时，对中状态和倾斜状态下最小油膜厚度增加；相同转速下，考虑轴倾斜时最小油膜厚度减小，最小油膜厚度值降低约5.5%，轴转速为1500~3000 r/min时，倾斜状态下最小油膜厚度降低百分比值保持不变，可以通过对中状态下最小油膜厚度来估算倾斜状态下的最小油膜厚度.
4. 结 语
1)轴承与轴颈对中状态下，油膜压力分布沿轴向对称；倾斜状态下，油膜压力分布沿轴向不对称，流场压力峰值增大，压力峰值位置靠近轴承端面，随转速增加，轴线方向上节点压力值增加.
2)本算例中，轴转速为1500~3000 r/min时，倾斜状态相对于对中状态，最小的油膜厚度值减少约5.5%，且保持不变，倾斜状态下的最小油膜厚度可以用对中状态下的最小油膜厚度来估算.
3)通过对滑动轴承的瞬态分析可以实时预测轴心坐标、油膜压力分布和油膜厚度等，为滑动轴承的优化设计提供参考.
-
图 7 沿轴线方向节点压力随转速变化曲线
Figure 7. Curve of nodal pressure along Z direction at different rotation speeds
-
[1] MUKHERJEE A, RAO J S. Stiffness and damping coefficients of an inclined journal bearing[J] . Mechanism and Machine Theory,1977,12(4):339 − 355. doi: 10.1016/0094-114X(77)90010-6 [2] 孙丽军, 薛闯, 张立浩, 等. 倾斜轴颈重载轴承润滑性能分析及试验研究[J] . 润滑与密封,2016,41(7):107 − 111. doi: 10.3969/j.issn.0254-0150.2016.07.019 [3] ZHU S Y, SUN J, LI B, et a1. Thermal turbulent lubrication analysis of rough surface journal bearing with joumal misalignment[J] . Tribology International,2020,144:12. [4] 王亚兵, 刘洋洋, 王报龙, 等. 轴颈倾斜的水润滑橡胶艉轴承的静态特性[J] . 西安交通大学学报,2020,54(5):61 − 69. doi: 10.7652/xjtuxb202005009 [5] SUN J, GUI C L. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation[J] . Tribology International,2004,37(10):841 − 848. doi: 10.1016/j.triboint.2004.05.007 [6] LYU F R, JIAO C X, TA N, et al. Mixed-lubrication analysis of misaligned bearing considering turbulence[J] . Tribology International,2018,119:19 − 26. doi: 10.1016/j.triboint.2017.10.030 [7] LYU F R, ZOU D L, TA N, et a1. Influence of local turbulent flow on the performance of a mixed-lubrication bearing[J] . Proceedings of the Institution of Mechanical Engineers: Part J Journal of Engineering Tribology,2019,233(208/209/210):1029 − 1035. doi: 10.1177/1350650118818303 [8] 刘洋洋, 王亚兵, 祝长生, 等. 考虑轴颈倾斜的水润滑橡胶径向轴承的动力学特性[J] . 西安交通大学学报,2021, 55(1):101 − 108. doi: 10.7652/xjtuxb202101013 [9] GERTZOS K P, NIKOLAKOPOULOS P G, PAPADOPOULOS C A. CFD analysis of journal bearing hydrodynamic lubrication by Bingham lubricant[J] . Tribology International,2008,41(12):1190 − 1204. doi: 10.1016/j.triboint.2008.03.002 [10] MERUANE V, PASCUAL R. Identification of nonlinear dynamic coefficients in plain journal bearings[J] . Tribology International,2008,41(8):743 − 754. doi: 10.1016/j.triboint.2008.01.002 [11] LIU H P, XU H, ELLISON P J, et al. Application of computational fluid dynamics and fluid–structure interaction method to the lubrication study of a rotor–bearing system[J] . Tribology Letters,2010,38(3):325 − 336. doi: 10.1007/s11249-010-9612-6 [12] LIN Q Y, BAO Q K, LI K J, et al. An investigation into the transient behavior of journal bearing with surface texture based on fluid-structure interaction approach[J] . Tribology International,2018,118:246 − 255. [13] LIN Q Y, WEI Z Y, WANG N, et al. Analysis on the lubrication performances of journal bearing system using computational fluid dynamics and fluid-structure interaction considering thermal influence and cavitation[J] . Tribology International,2013,64:8 − 15. [14] 孙加丰. 基于压电薄膜传感器的滑动轴承动油膜压力分布实时测量方法研究[D]. 上海: 上海交通大学, 2013. [15] 朱希玲, 荆建平. 基于气穴模型的动压轴承动态油膜刚度计算方法[J] . 润滑与密封,2019,44(9):120 − 125. doi: 10.3969/j.issn.0254-0150.2019.09.020 [16] 刘鸿文. 材料力学[M]. 5版. 北京: 高等教育出版社, 2011: 125−126. 期刊类型引用(0)
其他类型引用(2)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 318
- HTML全文浏览量: 303
- PDF下载量: 96
- 被引次数: 2
