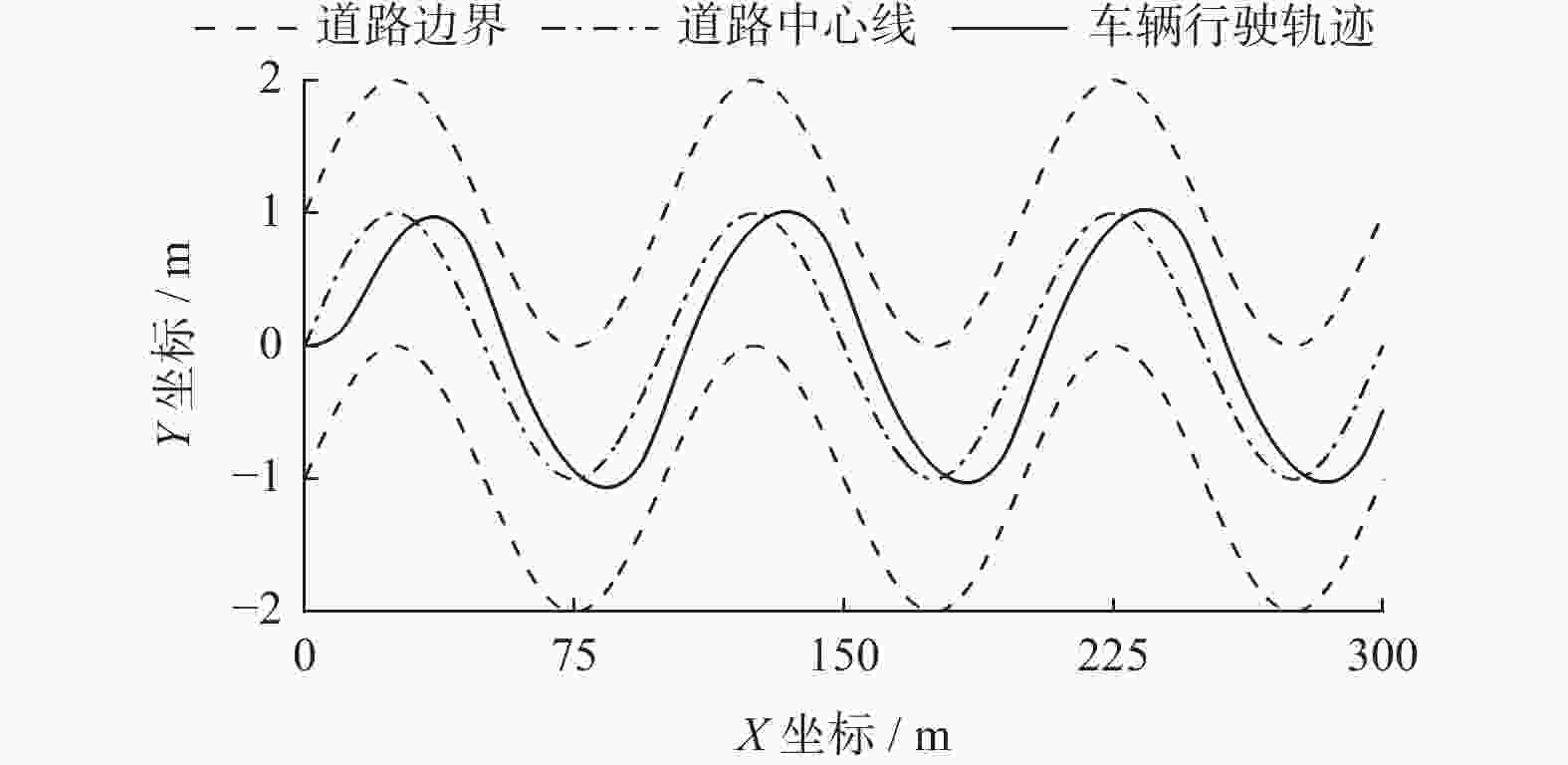
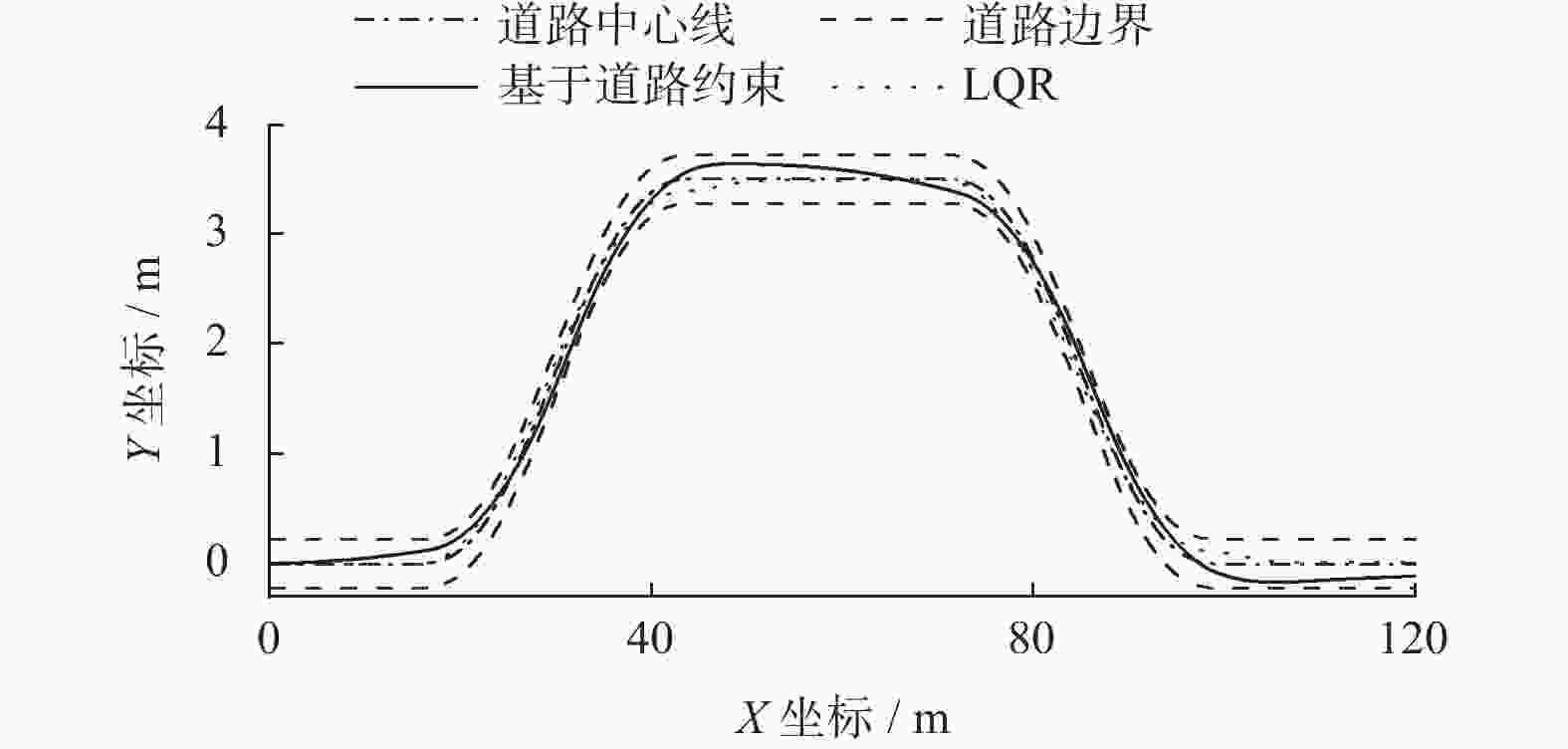
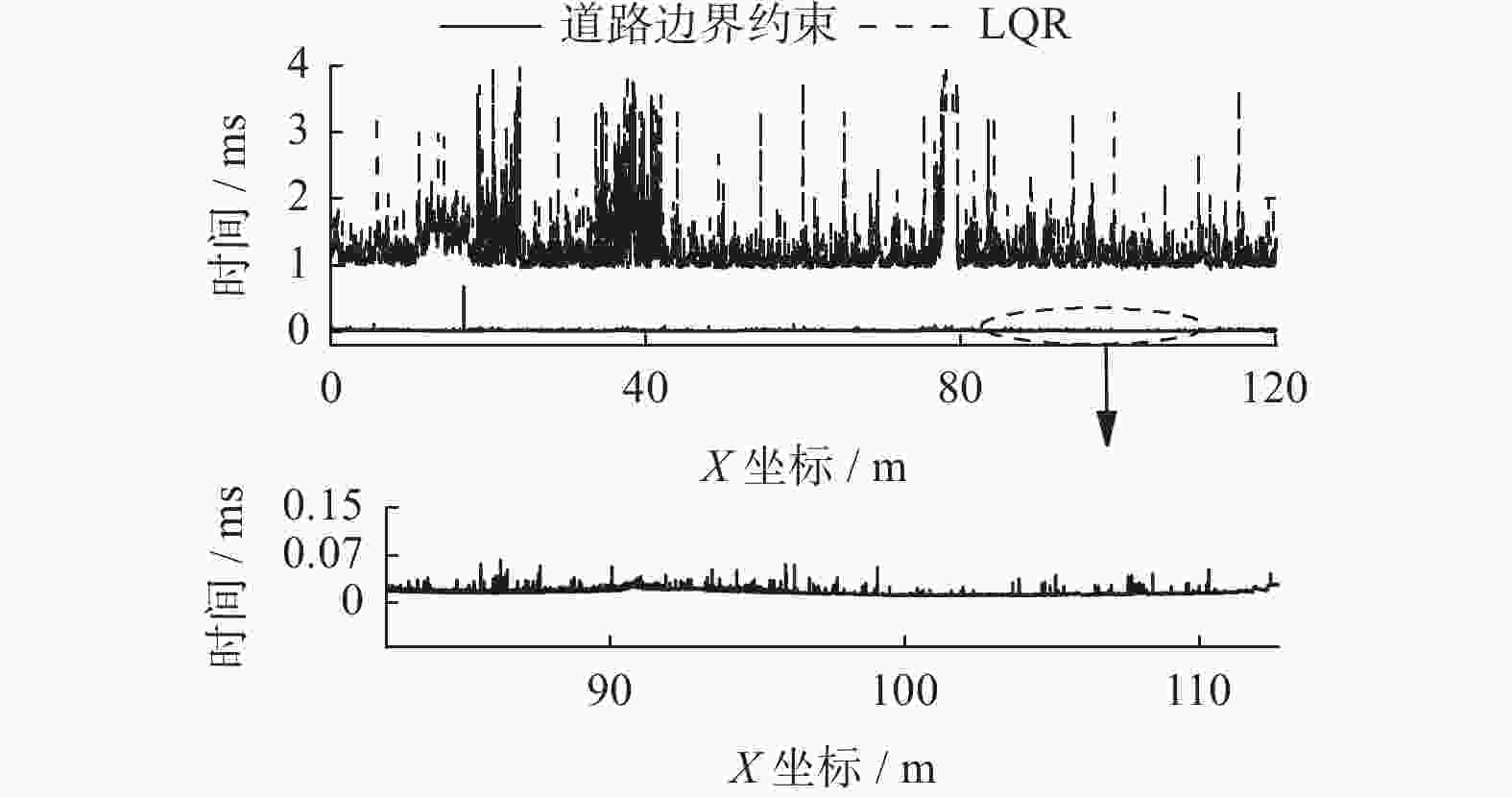
Vehicle lateral and longitudinal control based on road boundary constraints
-
摘要:
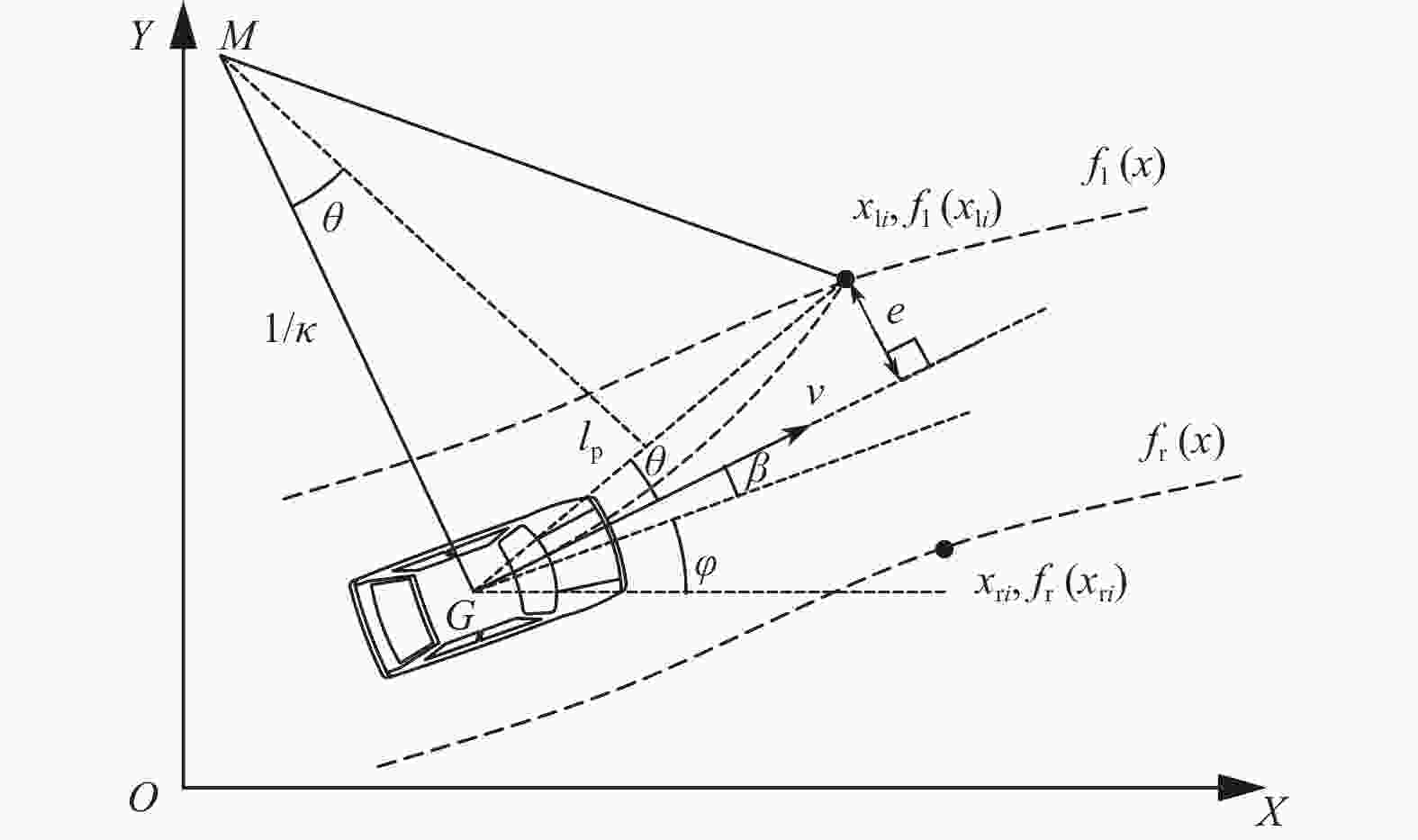
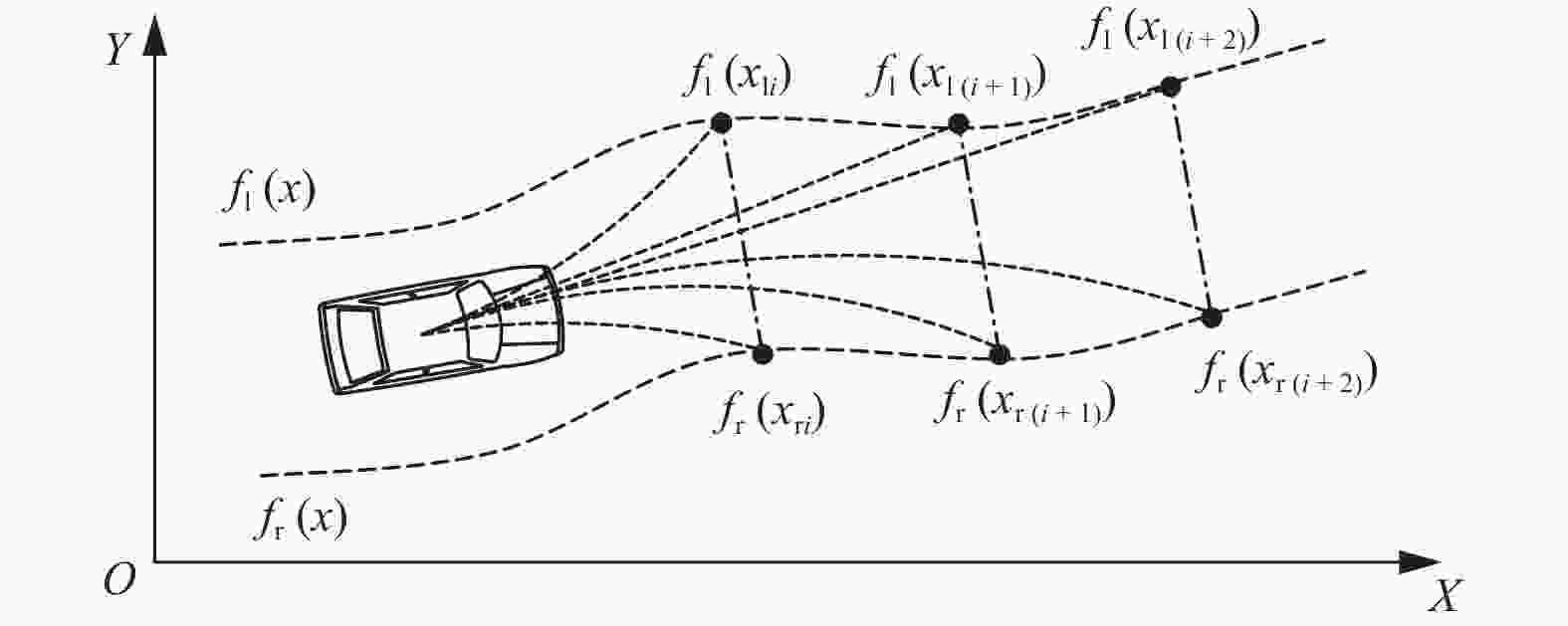
为提高自动驾驶车辆对不同道路的适应性和跟踪稳定性，提出一种基于道路边界约束和双比例−积分−微分(PID)的横纵向轨迹跟踪方法. 基于道路边界约束，求出使车辆安全行驶的转向曲率，结合二自由度动力学模型计算安全行驶转向角. 该方法计算简单，且最远预瞄点由道路的宽度及曲率信息自主确定. 通过仿真试验，制作车辆加速度、速度、油门和刹车的标定关系表，并基于标定表设计双PID速度跟踪控制器. 最后通过Carsim−Simulink联合仿真，证明横纵向控制器可以安全地行驶在道路范围内，并有良好的跟踪精度和稳定性.
Abstract:In order to improve the adaptability and tracking stability of autonomous vehicles to different roads, a lateral and longitudinal trajectory tracking method based on road boundary constraints and dual proportional-integral-derivative (PID) was proposed. Based on the road boundary constraints, the steering curvature for safe driving was obtained, and then the safe driving steering angle was calculated by combining the two-degree-of-freedom dynamic model. The method is simple to calculate, and the farthest preview point is determined autonomously by the width and curvature information of the road. Through the simulation test, the calibration relationship table of vehicle acceleration, speed, accelerator and brake were made, and a dual-PID speed tracking controller was designed based on the calibration table. Finally, through the Carsim-Simulink co-simulation, it is proved that the lateral and longitudinal controller can safely drive within the road range, and has good tracking accuracy and stability.
-
图 3 道路边界限制转换为曲率约束的方法示意图
Figure 3. Schematic diagram of the method for converting road boundary constraints to curvature constraints
图 4 由近到远选取预瞄点示意图
Figure 4. Schematic diagram of selecting preview points from near to far
表 1 仿真参数
Table 1. Simulation parameters
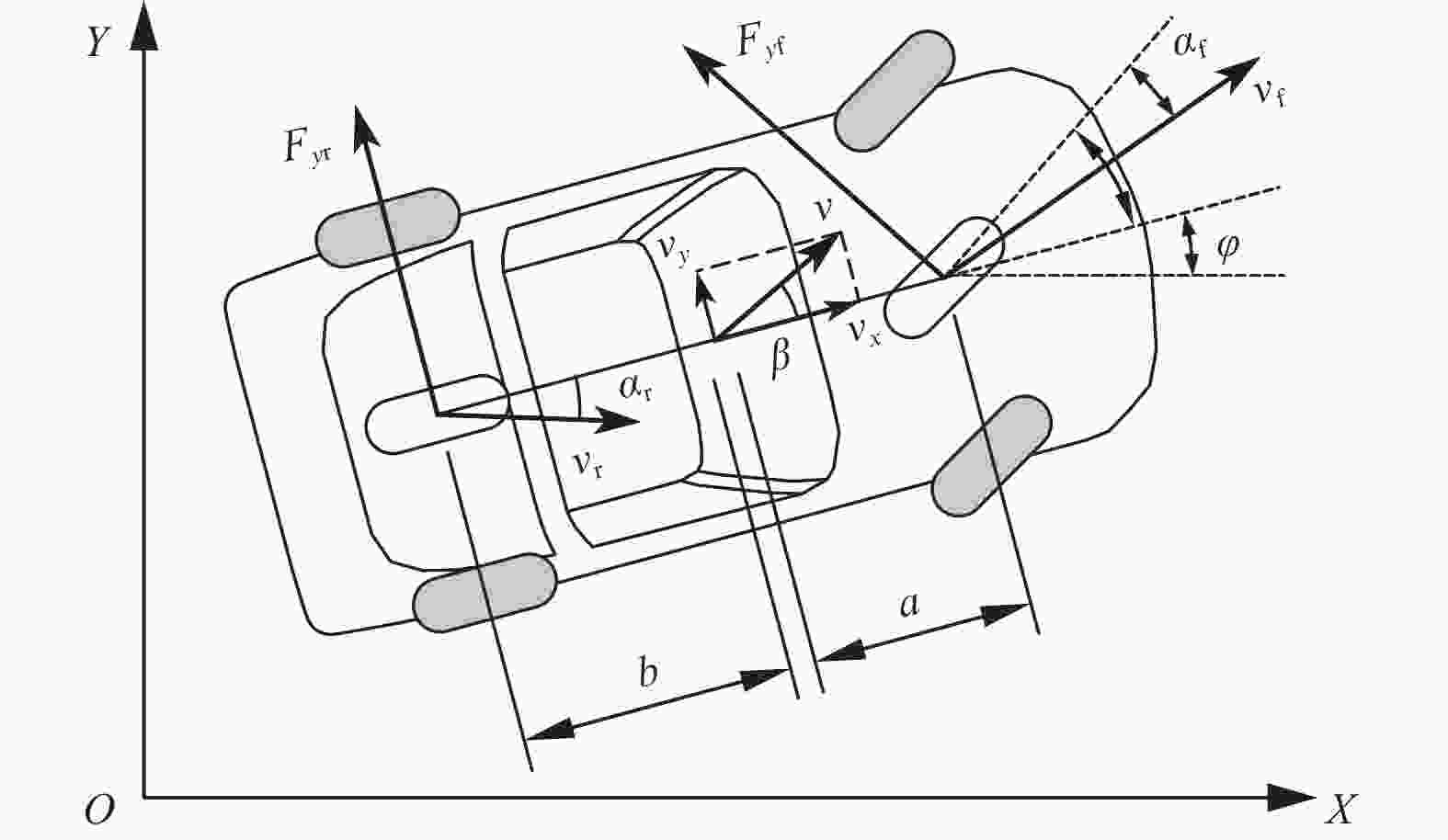
定义 符号 值 整车质量/kg $ m $ 1412 质心到前轴距离/m $ a $ 1.015 质心到后轴距离/m $ b $ 1.895 前轮侧偏刚度/$({\text{N} }·{\text{ra} }{ {\text{d} }^{ { { - 1} } } })$ ${C_{\alpha {\rm{f}}} }$ −148970 后轮侧偏刚度/$({\text{N} }·{\text{ra} }{ {\text{d} }^{ { { - 1} } } })$ ${C_{\alpha {\rm{r}}} }$ −82204 
下载: 导出CSV
-
[1] CHEN Y M, HU C, WANG J M. Human-centered trajectory tracking control for autonomous vehicles with driver cut-in behavior prediction[J] . IEEE Transactions on Vehicular Technology,2019,68(9):8461 − 8471. doi: 10.1109/TVT.2019.2927242 [2] HUANG Y J, DING H T, ZHANG Y B, et al. A motion planning and tracking framework for autonomous vehicles based on artificial potential field elaborated resistance network approach[J] . IEEE Transactions on Industrial Electronics,2020,67(2):1376 − 1386. doi: 10.1109/TIE.2019.2898599 [3] THRUN S, MONTEMERLO M, DAHLKAMP H, et al. Stanley: The robot that won the darpa grand challenge[J] . Journal of field Robotics,2006,23(9):661 − 692. doi: 10.1002/rob.20147 [4] NORMEY-RICO J E, ALCALÁ I, GÓMEZ-ORTEGA J, et al. Mobile robot path tracking using a robust pid controller[J] . Control Engineering Practice,2001,9(11):1209 − 1214. doi: 10.1016/S0967-0661(01)00066-1 [5] 彭传颂, 赖杰, 潘鲁彬. 基于lqr与前向增益的无人车辆轨迹跟踪控制[J] . 农业装备与车辆工程,2021,59(4):40 − 43. [6] HU C, CHEN Y M, WANG J M. Fuzzy observer-based transitional path-tracking control for autonomous vehicles[J] . IEEE Transactions on Intelligent Transportation Systems,2021,22(5):3078 − 3088. doi: 10.1109/TITS.2020.2979431 [7] HU C, WANG Z F, QIN Y C, et al. Lane keeping control of autonomous vehicles with prescribed performance considering the rollover prevention and input saturation[J] . IEEE Transactions on Intelligent Transportation Systems,2020,21(7):3091 − 3103. doi: 10.1109/TITS.2019.2924937 [8] GUO N Y, LENZO B, ZHANG X D, et al. A real-time nonlinear model predictive controller for yaw motion optimization of distributed drive electric vehicles[J] . IEEE Transactions on Vehicular Technology,2020,69(5):4935 − 4946. doi: 10.1109/TVT.2020.2980169 [9] 谢辉, 刘爽爽. 基于模型预测控制的无人驾驶汽车横纵向运动控制[J] . 汽车安全与节能学报,2019,10(3):326 − 333. doi: 10.3969/j.issn.1674-8484.2019.03.008 [10] 陈无畏, 谈东奎, 汪洪波, 等. 一类基于轨迹预测的驾驶员方向控制模型[J] . 机械工程学报,2016,52(14):106 − 115. [11] 李红志, 李亮, 宋健, 等. 预瞄时间自适应的最优预瞄驾驶员模型[J] . 机械工程学报,2010,46(20):106 − 111. [12] CUI Q J, DING R J, WEI C F, et al. Path-tracking and lateral stabilisation for autonomous vehicles by using the steering angle envelope[J] . Vehicle System Dynamics,2021,59(11):1672 − 1696. doi: 10.1080/00423114.2020.1776344 [13] 张栩源, 李军. 基于lqr双pid的智能电动汽车轨迹跟踪横纵向协同控制[J] . 汽车安全与节能学报,2021,12(3):346 − 354. doi: 10.3969/j.issn.1674-8484.2021.03.009 -
下载:
点击查看大图
计量
- 文章访问数: 301
- HTML全文浏览量: 93
- PDF下载量: 50
- 被引次数: 0
