改进多步长蚁群算法移动机器人路径规划研究

马滕; 茅健

doi:10.12299/jsues.22-0174

改进多步长蚁群算法移动机器人路径规划研究

doi: 10.12299/jsues.22-0174

马滕,
茅健^,

上海工程技术学机械与汽车工程学院, 上海 201620

详细信息

作者简介:
马滕（1996−），男，在读硕士，研究方向为移动机器人路径规划. E-mail：ail：tmasues@163.com

通讯作者:
茅健（1972−），男，教授，博士，研究方向为精密检测与控制. E-mail：ail：jmao@sues.edu.cn

中图分类号: TP242
计量
- 文章访问数: 152
- HTML全文浏览量: 38
- PDF下载量: 26
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-01
- 刊出日期: 2023-09-30

Research on path planning of mobile robot based on improved multi-step ant colony algorithm

MA Teng,
MAO Jian^,

School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

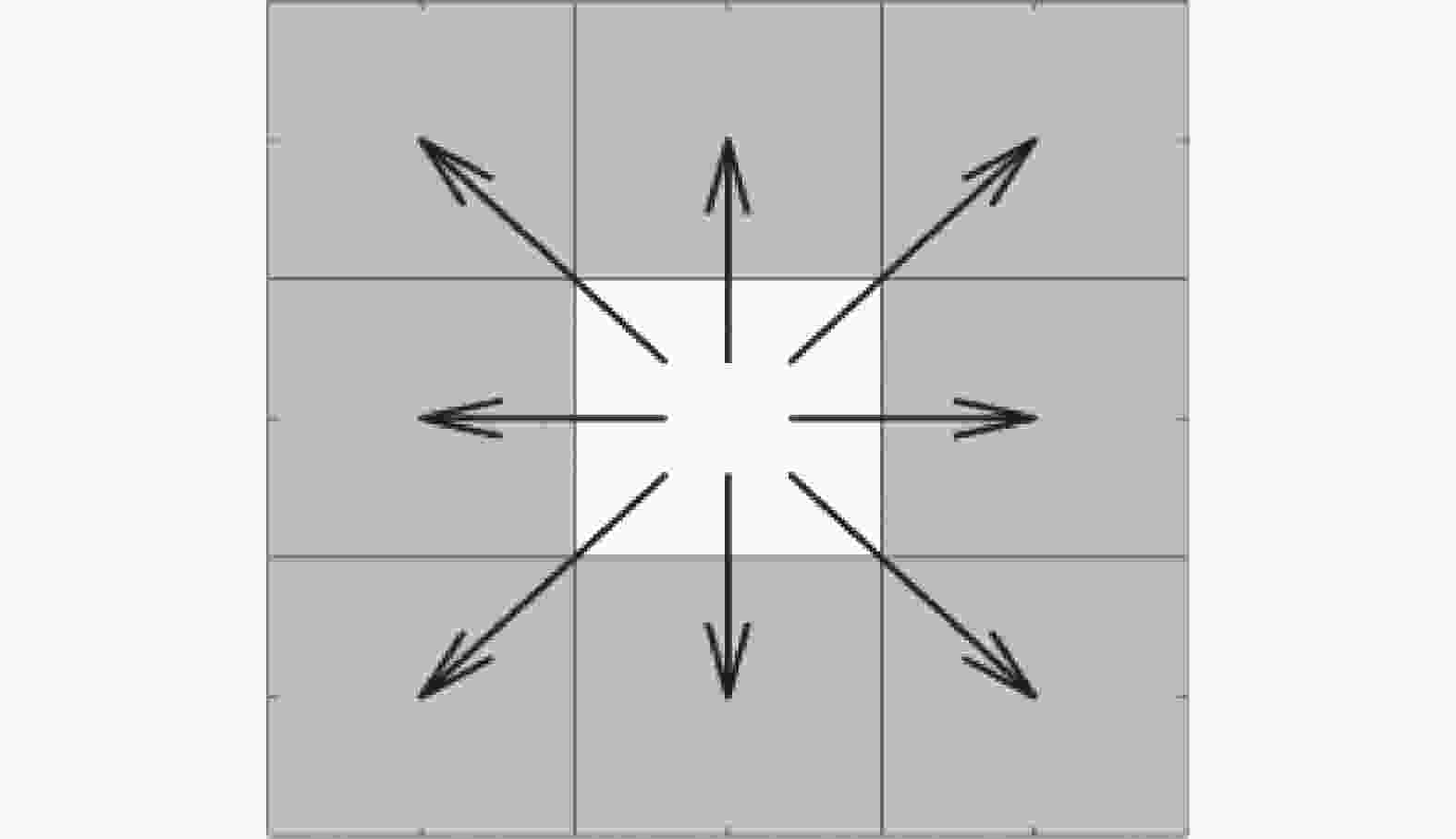
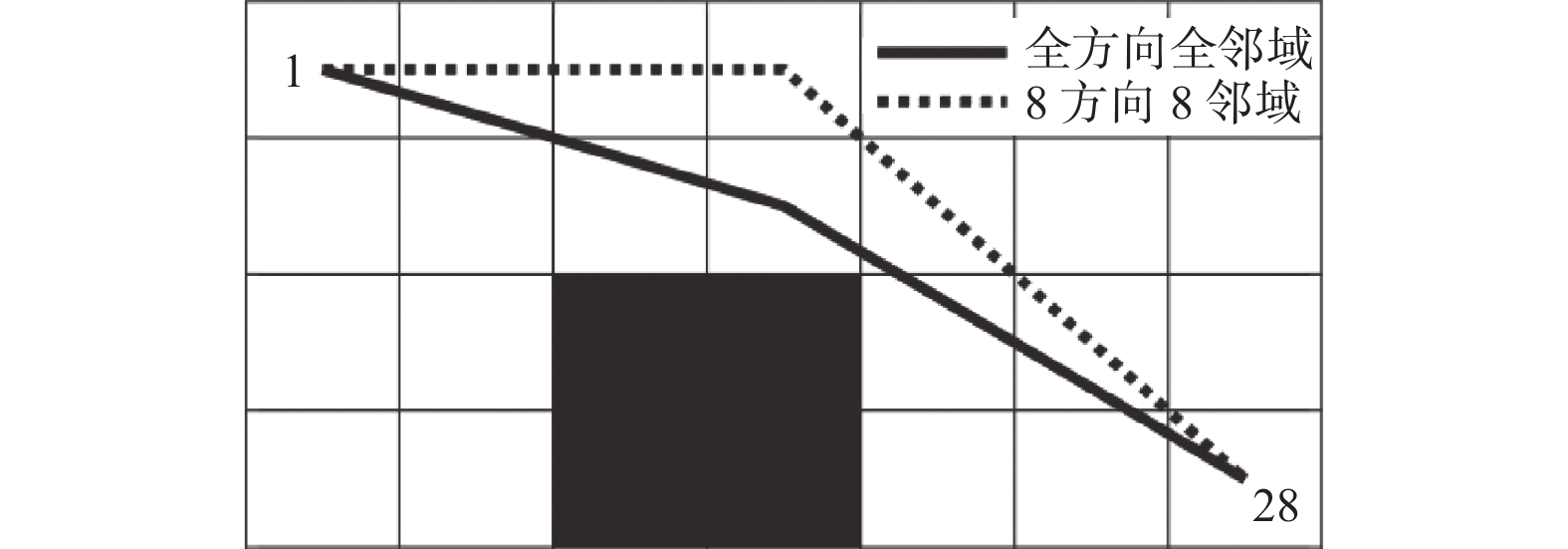
摘要: 为改善传统蚁群算法在路径规划中存在的规划路径实用性差、收敛速度慢、易陷入局部最优等问题，提出一种改进多步长蚁群算法. 改进算法以移动机器人视野域内所有可直达节点作为下一步可选节点集，采用多步长移动方式以任意方向任意步长寻找下一节点，提高算法寻优效率和路径规划多样性；节点之间初始信息素依各节点与当前节点和目标节点连线的距离采取不均匀分布，降低蚁群在算法初期搜索的盲目性；通过路径长度增大优质路径与劣质路径的信息素更新差距，改进启发函数，提高算法收敛速度. 仿真结果表明，改进算法规划路径具有长度短、路径平滑度高、步数少的优点，更符合移动机器人实际使用需求，收敛速度明显加快，路径规划效果提升显著.
- 路径规划 /
- 蚁群算法 /
- 多步长 /
- 路径平滑度 /
- 信息素
Abstract: Improved multi-step ant colony algorithm was proposed to solve the problems of traditional ant colony algorithm in path planning, such as poor practicability, slow convergence speed and local optimization. All the direct nodes in the field of view of the mobile robot for the improved algorithm were taken as the next optional node set, the multi-step moving method was used to find the next node in any direction and at any step length, and the optimization efficiency of the algorithm and the diversity of path planning was improved. The initial pheromones among nodes were unevenly distributed according to the distance between each node and the connecting line between current and target node, the blindness of ant colony search in the initial stage of the algorithm was reduced. By increasing the pheromone update gap between the high-quality path and the low-quality path through the path length, the heuristic function and the convergence speed of the algorithm was improved. The simulation results show that the improved algorithm has the advantages of short length, high smoothness and less steps, which are more in line with the actual needs of mobile robots. The convergence speed and the effect of path planning are significantly improved.
- path planning /
- ant colony algorithm /
- multi-step /
- path smoothness /
- pheromone

HTML全文

图 1 栅格地图

Figure 1. Grid map

下载: 全尺寸图片幻灯片

图 2 8方向8邻域搜索方式

Figure 2. 8-direction 8-neighborhood search method

下载: 全尺寸图片幻灯片

图 3 两种搜索方式规划路径

Figure 3. Two search methods for path planning

下载: 全尺寸图片幻灯片

图 4 路径平滑度

Figure 4. Path smoothness

下载: 全尺寸图片幻灯片

图 5 可选节点集

Figure 5. Optional node set

下载: 全尺寸图片幻灯片

图 6 初始信息素不均匀分布

Figure 6. Uneven distribution of initial pheromone

下载: 全尺寸图片幻灯片

图 7 最短路径比较

Figure 7. Shortest path comparison

下载: 全尺寸图片幻灯片

图 8 20 × 20地图模型仿真结果

Figure 8. 20 × 20 map model simulation results

下载: 全尺寸图片幻灯片

图 9 最优路径仿真结果对比

Figure 9. Comparison of optimal path simulation results

下载: 全尺寸图片幻灯片

图 10 30 × 30地图模型仿真结果

Figure 10. 30 × 30 map model simulation results

下载: 全尺寸图片幻灯片

表 1 各参数不同取值实验结果

Table 1. Experimental results of different values of parameters

参数	参数设定值及实验结果
$ \alpha $	0.5	1.0	1.5	2.0	3.0
路径长度均值	29.73	29.68	29.40	30.17	30.76
平均收敛迭代次数	39.3	13.6	4.2	7.9	7.0
$ \beta $	1	3	5	7	10
路径长度均值	32.92	32.86	32.90	30.98	33.38
平均收敛迭代次数	8.3	14.9	8.6	6.6	9.8
$ \rho $	0.1	0.3	0.5	0.7	0.9
路径长度均值	32.88	32.93	33.07	32.84	33.05
平均收敛迭代次数	21.8	19.4	9.7	8.5	9.8
$ x $	2	3	4	5	6
路径长度均值	33.08	32.87	32.71	32.62	33.11
平均收敛迭代次数	12.4	9.7	7.9	6.8	6.3

下载: 导出CSV

表 2 各参数设置

Table 2. Parameter settings

参数	参数值
最大迭代次数 N_cmax	100
蚂蚁数量 M	50
信息素重要程度因子$ \alpha $	1.5
启发函数重要程度因子$ \beta $	7
信息素挥发系数$ \rho $	0.7
信息素强度 Q	1
信息素更新放大控制因子$ x $	5

下载: 导出CSV

表 3 20 × 20栅格地图仿真数据

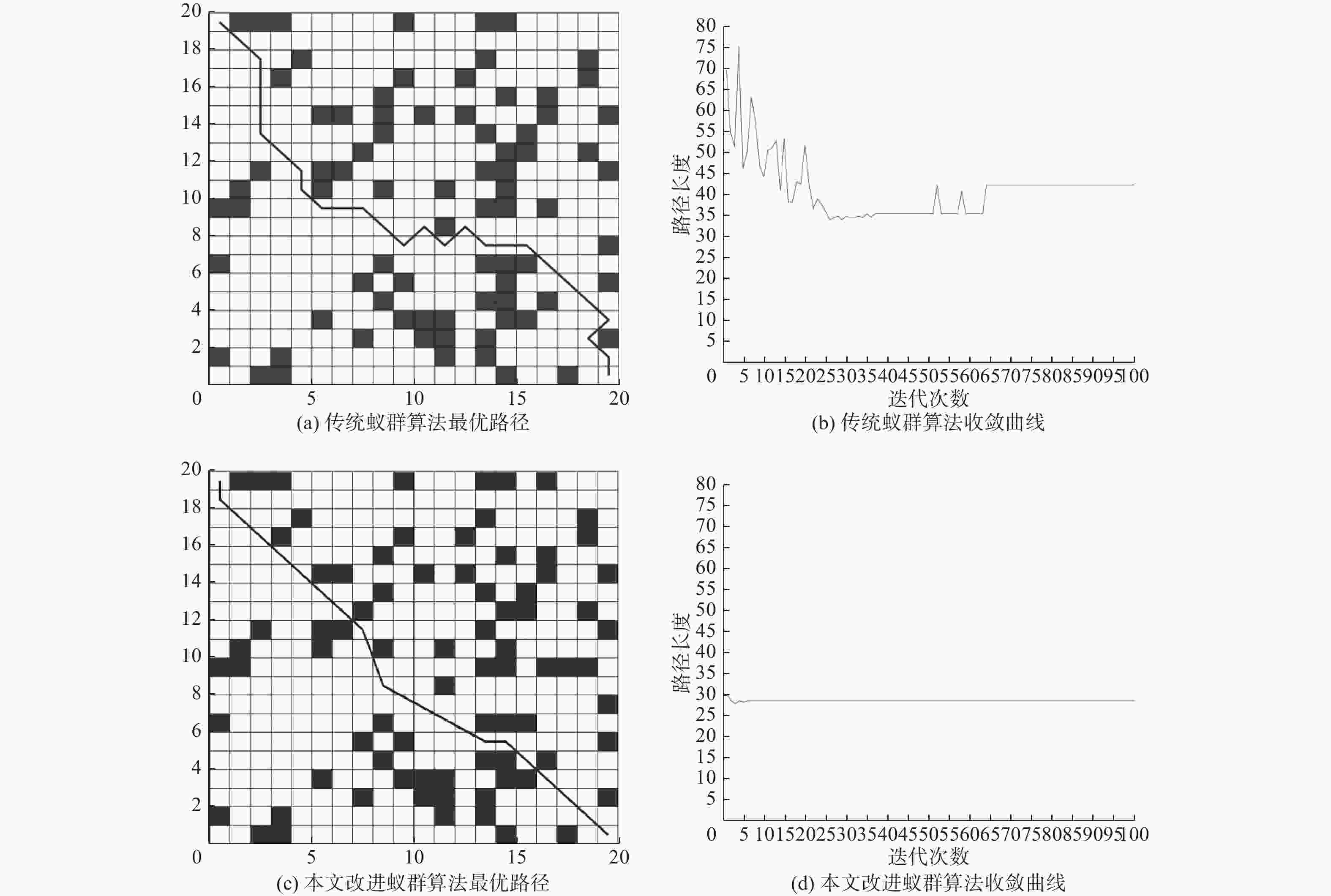
Table 3. 20 × 20 grid map simulation data

算法	路径平均长度	平均收敛迭代次数	路径平均转弯次数	最优路径长度	最优路径转弯次数	最优路径迭代次数
传统蚁群算法	35.25	57.6	16.8	34.04	15	64
本研究改进算法	28.40	5.2	3.7	27.96	5	6

下载: 导出CSV

表 4 30 × 30栅格地图仿真数据

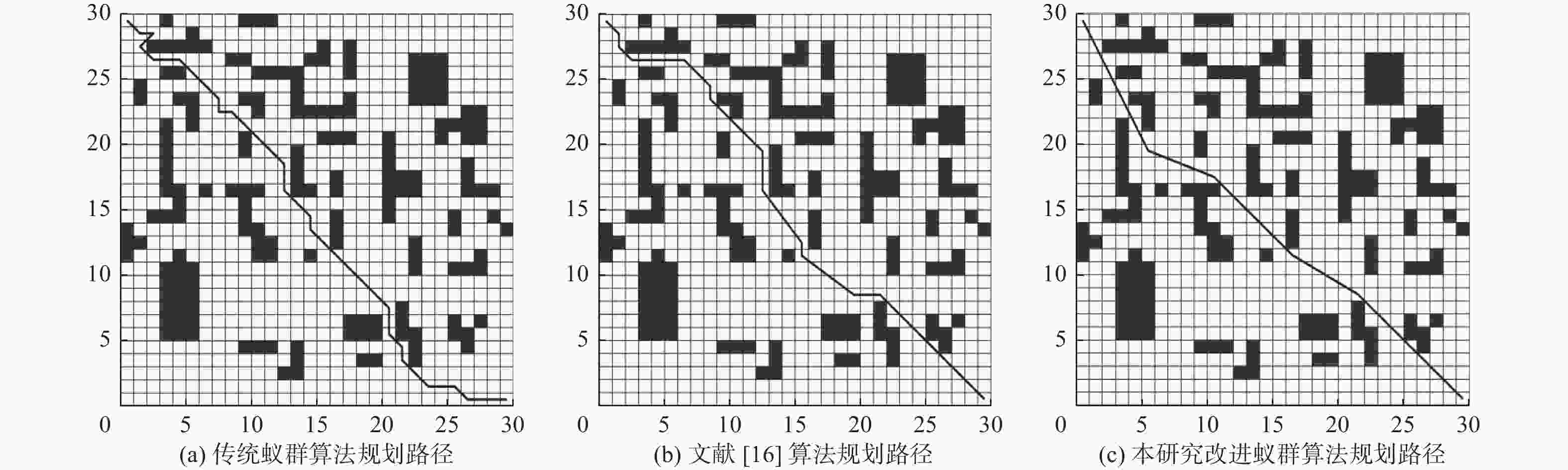
Table 4. 30 × 30 grid map simulation data

算法	最优路径长度	路径转弯次数	收敛迭代次数
传统蚁群算法	47.11	19	68
文献[16]算法	44.53	12	9
本研究改进蚁群算法	42.20	4	6

下载: 导出CSV

参考文献(16)

[1]	LIU J H, YANG J G, LIU H P, et al. An improved ant colony algorithm for robot path planning[J] . Soft Computing,2016,21(19):1 − 11.
[2]	陈继清, 谭成志, 莫荣现, 等. 基于人工势场的A ~ *算法的移动机器人路径规划[J] . 计算机科学,2021,48(11):327 − 333. doi: 10.11896/jsjkx.200900170
[3]	刘子豪, 赵津, 刘畅, 等. 基于改进A*算法室内移动机器人路径规划[J] . 计算机工程与应用,2021,57(2):186 − 190.
[4]	LUO M, HOU X, YANG J. Surface optimal path planning using an extended Dijkstra algorithm[J] . IEEE Access,2020,8:147827 −38.
[5]	MUR-ARTAL R, MONTIEl J M M, TARDOS J D. ORB-SLAM: A versatile and accurate monocular SLAM system[J] . IEEE Transactions on Robotics,2015,31(5):1147 − 1163. doi: 10.1109/TRO.2015.2463671
[6]	张菁, 何友, 彭应宁, 等. 基于神经网络和人工势场的协同博弈路径规划[J] . 航空学报,2019,40(3):228 − 238.
[7]	高岳林, 武少华. 基于自适应粒子群算法的机器人路径规划[J] . 郑州大学学报(工学版),2020,41(4):46 − 51.
[8]	巫光福, 万路萍. 粒子群算法优化机器人路径规划的研究[J] . 机械科学与技术,41,11:1759 − 1764.
[9]	杨立炜, 付丽霞, 王倩, 等. 多层优化蚁群算法的移动机器人路径规划研究[J] . 电子测量与仪器学报,2021,35(9):10 − 18. doi: 10.13382/j.jemi.B2104304
[10]	张晓莉, 杨亚新, 谢永成. 改进的蚁群算法在机器人路径规划上的应用[J] . 计算机工程与应用,2020,56(2):29 − 34. doi: 10.3778/j.issn.1002-8331.1907-0104
[11]	曾明如, 徐小勇, 罗浩, 等. 多步长蚁群算法的机器人路径规划研究[J] . 小型微型计算机系统,2016,37(2):366 − 369. doi: 10.3969/j.issn.1000-1220.2016.02.033
[12]	许凯波, 鲁海燕, 黄洋, 等. 基于双层蚁群算法和动态环境的机器人路径规划方法[J] . 电子学报,2019,47(10):2166 − 2176. doi: 10.3969/j.issn.0372-2112.2019.10.019
[13]	张恒, 何丽, 袁亮, 等. 基于改进双层蚁群算法的移动机器人路径规划[J] . 控制与决策,2022,37(2):303 − 313.
[14]	史恩秀, 陈敏敏, 李俊, 等. 基于蚁群算法的移动机器人全局路径规划方法研究[J] . 农业机械学报,2014,45(6):53 − 57. doi: 10.6041/j.issn.1000-1298.2014.06.009
[15]	袁福龙, 朱建平. 基于改进蚁群算法的移动机器人最优路径规划[J] . 现代制造工程,2021(7):38 − 47,65. doi: 10.16731/j.cnki.1671-3133.2021.07.006
[16]	马小陆, 梅宏. 基于改进势场蚁群算法的移动机器人全局路径规划[J] . 机械工程学报,2021,57(1):19 − 27.