Fe-Ti二元系热力学评估比较

金宗啸; 苏钰; 李军; 杨慧文

doi:10.12299/jsues.22-0254

Fe-Ti二元系热力学评估比较

doi: 10.12299/jsues.22-0254

上海工程技术大学材料科学与工程学院, 上海 201620

基金项目: 国家自然科学基金项目资助（51301105、51471105）；上海市自然科学基金项目资助（20ZR1422200）

详细信息

作者简介:
金宗啸（1998−），男，在读硕士，研究方向为CALPHAD优化方法. E-mail：1727756490@qq.com

通讯作者:
苏　钰（1977−），女，副教授，博士，研究方向为材料计算与金属强韧性. E-mail：suyu@sues.edu.cn

中图分类号: TG146.22
计量
- 文章访问数: 304
- HTML全文浏览量: 129
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-19
- 刊出日期: 2023-09-30

Comparison of Fe-Ti binary system thermodynamic assessments

School of Materials Science and Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

摘要: Fe-Ti二元系作为多组元Fe合金和多组元Ti合金的子系统，其热力学性质研究是将其拓展到多维应用的基础. 利用CALPHAD方法，选取近几十年来最具代表性的5篇Fe-Ti二元系评估研究论文，复现各评估研究的计算结果，比较不同评估对稳定相的热力学建模的相异性和对最终评估结果的影响，同时指出某些评估中存在的问题.
- Fe-Ti二元系 /
- 热力学评估 /
- 亚点阵模型 /
- CALPHAD方法 /
- 相稳定性
Abstract: As a subsystem of multi-principal-elements Fe alloys and multi-principal-elements Ti alloys, the thermodynamic properties of the Fe-Ti binary system are the basis for expanding it to multi-dimensional applications. By using CALPHAD method, five of the most representative Fe-Ti binary system assessment research articles in recent decades were selected and the calculation conclusions of these research were reproduced. Meanwhile, the dissimilarities of the thermodynamic modeling of stable phases of different assessments and the impact on the final evaluation results were compared, and some problems in the evaluation were pointed out.
- Fe-Ti binary system /
- thermodynamic assessment /
- sublattice model /
- CALPHAD method /
- phase stability

HTML全文

图 1 1 873 K时，Fe-Ti二元系液相混合焓

(a) Kumar等^[2]、Dumitrescu等^[4]、Wang等^[9]、Thiedemann等^[10]试验数据 (b) Bo等^[6]、Kriegel等^[8]、Wang等^[9]、Thiedemann等^[10]试验数据

Figure 1. Enthalpy of mixing in liquid phase at 1 873 K of Fe-Ti system

下载: 全尺寸图片幻灯片

图 2 1 873 K时，Fe-Ti二元系中Fe、Ti在液相中的活度

（a） Kumar等^[2]、Dumitrescu等^[4]、Furukawa等^[11]、Fruehan^[12]试验数据（b） Bo等^[6]、Kriegel等^[8]、Furukawa等^[11]、Fruehan^[12]试验数据

Figure 2. Activity of Fe and Ti in liquid phase at 1 873 K of Fe-Ti system

下载: 全尺寸图片幻灯片

图 3 文献中计算的生成焓

Figure 3. Calculated enthalpy of formation in the literatures

下载: 全尺寸图片幻灯片

图 4 Fe-Ti二元计算相图与试验数据对比图

Figure 4. Comparison of calculated value of Fe-Ti binary phase diagram with experimental data

下载: 全尺寸图片幻灯片

图 5 Fe-Ti二元系统中的富Ti侧平衡相图的试验数据

Figure 5. Experimental data of Ti-rich side phase diagram in Fe-Ti binary system

下载: 全尺寸图片幻灯片

图 6 Fe-Ti二元系统中的富Fe侧gamma-loop的试验数据

Figure 6. Experimental data of Gamma-loop at Fe-rich side in Fe-Ti binary system

下载: 全尺寸图片幻灯片

表 1 溶液相热力学参数计算值

Table 1. Calculated thermodynamic parameters of solution phase

相	参数	Kumar等^[2]	Jonsson^[3]	Dumitrescu等^[4]	Keyzer等^[5]	Bo等^[6]
LIQUID	L⁰	$ -6\;758 + 9.809T $	$ -64\;457 $	$ -71\;374 + 8.25T $	$ -76\;247 + 17.845T $	$ -74\;300 + 17.839T $
	L¹	$ -4\;731 $		$ 7\;434-4.5T $	$ 7\;900-6.069T $	$ 8\;299.849-6.101T $
	L²			$ 12\;155 + 0.25T $	$ 4\;345-2.844T $
BCC_A2	L⁰	$ -579 + 14.954T $	$ -58\;134 + 6.887T $	$ -59\;098 + 11.5T $	$ -68\;488 + 23.825T $	$ -69\;241.924 + 25.246T + $ $0.000\;1{T}^{2} + 120\;000{T}^{-1}$
	L¹	$ -6\;059 $	$ -12\;879 + 6.828T $	$ -1\;769 + T $	$ 5\;467-5.083T $	$ 5\;018.986-4.992T $
	L²			$ 5\;602 + 3.5T $	$ 25\;262-15.83T $	$ 23\;028.241-13.110T $
FCC_A1	L⁰	$ -5\;030 + 5.487T $	$ -50\;400 $	$ -51\;625 + 11T $	$ -56\;022 + 8.356T $	$ -52\;149.856 + 9.265T $
	L¹			$ -1\;950-6T $	$ 4\;773-4.029T $	$ 4\;755.9-4.982T $
	L²			$ 14\;875 $	$ 30\;021-12.614T $	$ 29\;205.228-11.046T $
HCP_A3	L⁰	$ 15\;132-8.668T $	$ -20\;019 + 23.08T $	$ -28\;750 + 11T $	$ -10\;000 + 15T $	$ -2\;500 + 35.004T $
	L¹			$ -1\;700-6T $
	L²			$ 15\;000 $

下载: 导出CSV

表 2 FeTi相热力学参数计算值

Table 2. Calculated thermodynamic parameters of FeTi phase

作者	FeTi相描述形式	热力学参数
Kumar等^[2]	化学计量化合物	$-53\;650 + 7.495T + {H}^{\mathrm{S}\mathrm{E}\mathrm{R} } + \displaystyle \sum { {}_{}{}^{0}G}^{\mathrm{S}\mathrm{E}\mathrm{R} }$
Jonsson^[3]	化学计量化合物	$-63\;646 + 243.681T-449\;929T{\rm{ln}}T-0.00\;843{T}^{2} + 102\;000{T}^{-1} + {H}^{\mathrm{S}\mathrm{E}\mathrm{R} }$
Dumitrescu等^[4]	化学计量化合物	$-90\;800 + 409T-73.5\;538T{\rm{ln}}T-0.01\;017{T}^{2} +$ $ 124\;200{T}^{-1} + {H}^{\mathrm{S}\mathrm{E}\mathrm{R}} $
Keyzer等^[5]	双亚点阵模型	${G}_{\mathrm{F}\mathrm{e}:\mathrm{T}\mathrm{i} }^{}=76\;218-46.685T + 8.663T\rm{ln}T-0.007\;151{T}^{2} + 1.121\;169{\text{×} } {10}^{-6}{T}^{3}$
Keyzer等^[5]	双亚点阵模型	$ {L}_{\mathrm{F}\mathrm{e},\mathrm{T}\mathrm{i}:\mathrm{F}\mathrm{e}}^{1}=-13\;764 $ $ {L}_{\mathrm{F}\mathrm{e},\mathrm{T}\mathrm{i}:Ti}^{0}=-6\;097 $ $ {L}_{\mathrm{F}\mathrm{e},\mathrm{T}\mathrm{i}:\mathrm{T}\mathrm{i}}^{1}=12\;256 $ $ {\mathrm{T}\mathrm{C}}_{\mathrm{B}2}=-1\;325 $
Bo等^[6]	双亚点阵模型	$ -30\;028.003 + 4.495T $
Bo等^[6]	双亚点阵模型	$ {L}_{\mathrm{F}\mathrm{e},\mathrm{T}\mathrm{i}:\mathrm{F}\mathrm{e}}=-5\;001.5 $ $ {L}_{\mathrm{F}\mathrm{e},\mathrm{T}\mathrm{i}:\mathrm{T}\mathrm{i}}=11\;000 $

下载: 导出CSV

表 3 Fe₂Ti相热力学参数计算值

Table 3. Calculated thermodynamic parameters of Fe₂Ti phase

作者	热力学模型	亚点阵点位	热力学参数
Kumar等^[2]	三亚点阵模型	Fe:Ti:Fe	$ -429\;782 + 120.875T $
		Fe:Fe:Fe	$ 69\;869 $
		Va:Ti:Fe	$-3\;556\;573 + 109.065T$
		Va:Fe:Fe	$ 60\;724 $
Josson^[3]	三亚点阵模型	Fe:Fe:Fe	$12{\text{×} }({}_{}{}^{0}{G}_{\mathrm{F}\mathrm{e} }^{} + 8\;426)$
		Fe:Ti:Fe	$12{\text{×} }(-34\;938 + 137.773-24.517\;77T\mathrm{l}\mathrm{n}T$ $-0.003\;39{T}^{2} + 41\;400{T}^{-1})$
		Fe:Fe:Ti	$2{G}_{\mathrm{F}\mathrm{e}:\mathrm{T}\mathrm{i}:\mathrm{F}\mathrm{e} }^{ {\mathrm{F}\mathrm{e} }_{2}\mathrm{T}\mathrm{i} }-{G}_{\mathrm{F}\mathrm{e}:\mathrm{T}\mathrm{i}:\mathrm{T}\mathrm{i} }^{ {\mathrm{F}\mathrm{e} }_{2}\mathrm{T}\mathrm{i} } + 2.4{\text{×} }{10}^{6} + 46.105T$
		Fe:Ti:Ti	$ 6{G}^{\mathrm{F}\mathrm{e}\mathrm{T}\mathrm{i}} + 28\;193 $
Dumitrescu等^[4]	双亚点阵模型	Fe:Fe	$ 15\;000 $
		Ti:Fe	$ 15\;000 $
		Fe:Ti	$-90\;800 + 409T-73.553\;18-0.010\;17{T}^{2}$ $ + 124\;200{T}^{-1} $
		Ti:Ti	$ 15\;000 $
		Fe,Ti:Va	$ -38\;000 $
		Va:Fe,Ti	$ 16\;000 $
Keyzer等^[5]	三亚点阵模型	摩尔吉布斯自由能函数G	$-78\;603 + 349.967\;5T-64.502T\mathrm{l}\mathrm{n}T$ $-0.0241\;491{T}^{2} + 3.936\;825{\text{×} }10^{-6}{T}^{3} + 7\;620{T}^{-1}$
		Fe,Ti:Fe:Fe	$ 3\;177 $
		Fe:Fe,Ti:Fe	$ 18\;000 $
		Fe:Fe:Fe,Ti	$ 6\;000 $
Bo等^[6]	双亚点阵模型	摩尔吉布斯自由能函数G	$ -85\;500 + 410.041T-73.553T\mathrm{l}\mathrm{n}T $ $-0.010\;17{T}^{2} + 124\;212.42{T}^{-1}$

下载: 导出CSV

表 4 Kriegel等^[8]计算的压力相关参数

Table 4. Pressure-related parameter calculated by Kriegel等^[8]

相	$ {\beta }_{0} $	$ {\beta }_{1} $	$ {\beta }_{2}^{} $	$ {\beta }_{3}^{} $	$ {K}_{T}^{\text{'}} $
FeTi	$5.164 \;3{\text{×} }{10}^{12}$	$9.329{\text{×} }{10}^{14}$	$-12.781 \;5{\text{×} }{10}^{19}$	$423.456{\text{×} }{10}^{23}$	$ 3.1 $
Fe₂Ti	$4.971 \;7{\text{×} }{10}^{12}$	$5.245{\text{×} }{10}^{14}$	$0.322 \;8{\text{×} }{10}^{19}$	$1.237 \;8{\text{×} }{10}^{23}$	$ 4 $

下载: 导出CSV

表 5 金属间相生成焓计算值与实验数据对比

Table 5. Comparation between calculated enthalpy of formation and experimental data in intermetallic phases

相	x(Ti)	温度/K	生成焓 $\Delta H$/(kJ•mol⁻¹)
相	x(Ti)	温度/K	Kumar等^[2]	Jonsson^[3]	Dumitrescu等^[4]	试验值及来源
FeTi	$0.500$	$ 1\;450 $	$ -27.51 $	$-31.691$	$ -29.868 $	$ -31.1 $，Gacchon等^[13]
FeTi	$0.500$	$ 1\;513 $	$ -27.29 $	$-31.639$	$ -29.816 $	$ -27.8 $，Dinsdale等^[14]
Fe₂Ti	$0.311$	$ 1\;514 $	$ -31.81 $	$-31.510$	$ -26.863 $	$ -27.6 $，Gacchon等^[13]
Fe₂Ti	$0.330$	$ 1\;413 $	$ -34.52 $	$-33.930$	$ -29.273 $	$ -25.4 $，Dinsdale等^[14]

下载: 导出CSV

表 6 Fe-Ti二元系中温度和摩尔分数计算值与试验测量值

Table 6. Calculated values and experimental measured value of temperature and mole fraction of Fe-Ti system

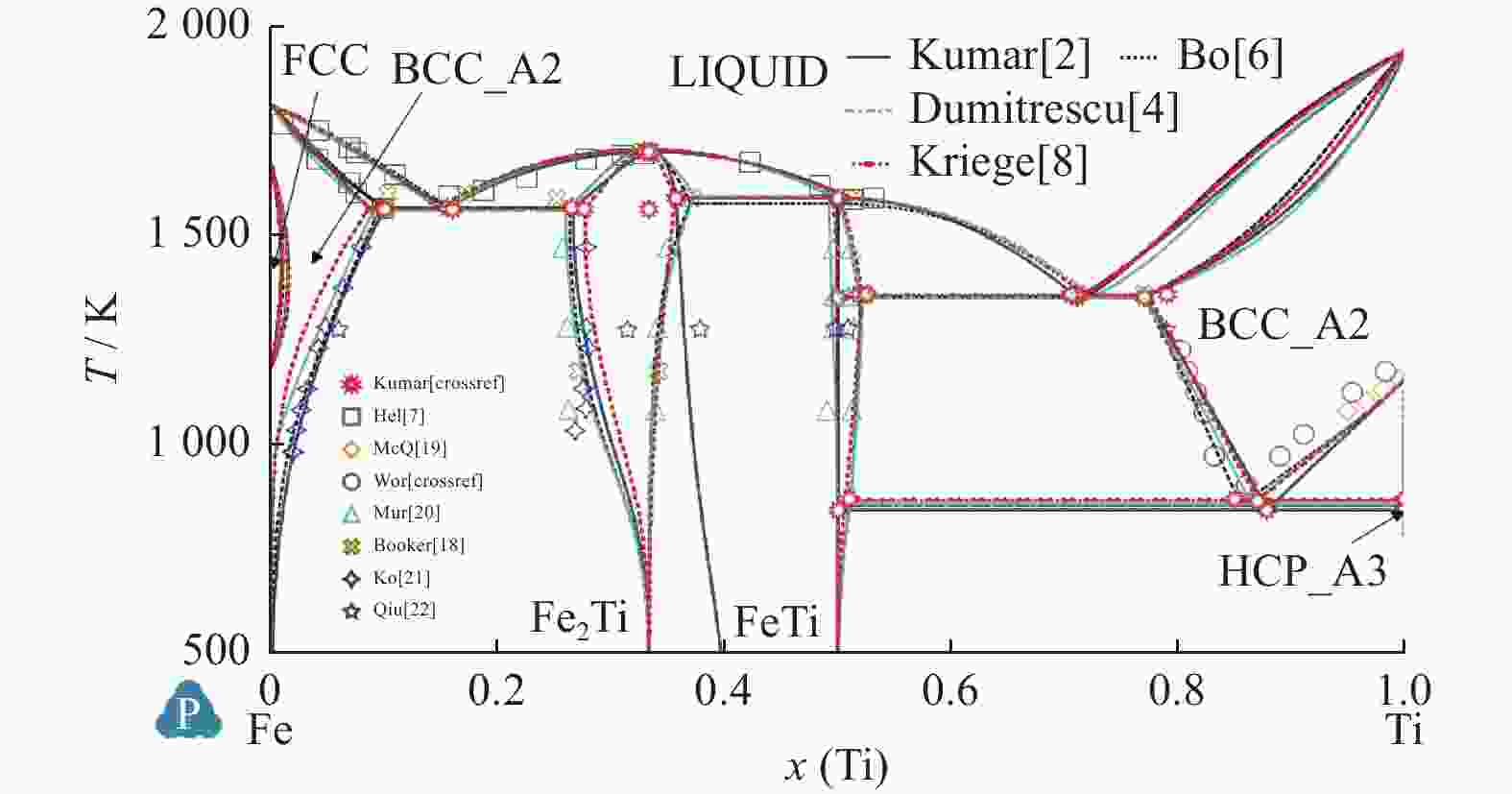
平衡反应	Kumar等^[2]	Jonsson^[3]	Dumitrescu等^[4]	Bo等^[6]	Kriegel等^[8]	试验^[15]	试验^[16]	试验^[17]
L$ \leftrightarrow $BCC_Fe + Fe₂Ti	T=1 565.4 K	T=1 564 K	T=1 562 K	T=1 559 K x(Ti)=0.26	T=1 564.3 K x(Ti)=0.277	T=1 562 K	T=1 599 K x_Ti=0.25
Cong.melt Fe₂Ti	T=1 699.5 K	T=1 704 K	T=1 692.5 K	T=1 706 K x(Ti)=0.329	T=1 700.8 K x(Ti)=0.333	T=1 700 K	T=1 696 K
FeTi$ \leftrightarrow $Fe₂Ti + L	T=1 589.5 K	T=1 593 K	T=1 612 K	T=1 592 K x(Ti)=0.492	T=1 588.4 K x(Ti)=0.356	T=1 590 K	T=1 589 K x(Ti)=0.37
L$ \leftrightarrow $FeTi + BCC_Ti	T=1 351 K	T=1 346 K	T=1 355 K	T=1 352 K x(Ti)=0.77	T=1 356.5 K x(Ti)=0.774			T=1 353 K x(Ti)=0.78
BCC_Ti$ \leftrightarrow $FeTi + HCP_Ti	T=840.65 K	T=859 K	T=856.4 K	T=856 K x(Ti)=0.9 995	T=864.8 K			T=848 K x(Ti)>0.99

下载: 导出CSV

参考文献(35)

[1]	KAUFMAN L, NESOR H. Coupled phase diagrams and thermochemical data for transition metal binary systems — I[J] . Calphad,1978,2(1):55 − 80. doi: 10.1016/0364-5916(78)90005-6
[2]	KUMAR K C H, WOLLAIITS P, DELAEY L. Thermodynamic reassessment and calculation of Fe-Ti phase diagram[J] . Calphad,1994,18(2):223 − 234. doi: 10.1016/0364-5916(94)90028-0
[3]	JONSSON S. Assessment of the Fe-Ti system[J] . Metallurgical and Materials Transactions B,1998,29(2):361 − 370. doi: 10.1007/s11663-998-0113-z
[4]	DUMITRESCU L F S, HILLERT M, SOUNDERS N. Comparison of Fe-Ti assessments[J] . Journal of Phase Equilibria,1998,19(5):441 − 448. doi: 10.1361/105497198770341923
[5]	De KEYZER J, CACCIAMANI G, DUPIN N, et al. Thermodynamic modeling and optimization of the Fe–Ni–Ti system[J] . Calphad,2009,33(1):109 − 123. doi: 10.1016/j.calphad.2008.10.003
[6]	BO H, WANG J, DUARTE L, et al. Thermodynamic re-assessment of Fe–Ti binary system[J] . Transactions of Nonferrous Metals Society of China,2012,22(9):2204 − 2211. doi: 10.1016/S1003-6326(11)61450-7
[7]	GRIMVALL G. Thermophysical Properties of Materials[M]. Elsevier, 1999. https://doi.org/10.1016/B978-044482794-4/50007-3.
[8]	KRIEGEL M J, WETZEL M H, FABRICHNAYA O, et al. Binary Ti–Fe system. Part II: Modelling of pressure-dependent phase stabilities[J] . Calphad,2022,76:102383. doi: 10.1016/j.calphad.2021.102383
[9]	WANG H, LÜCK R, PREDEL B. Calorimetric determination of the enthalpy of mixing of liquid iron-titanium alloys[J] . Zeitschrift fuer Metallkunde,1991,82(8):659 − 665.
[10]	THIEDEMANN U, QIN J, SCHAEFERS K, et al. Mixing enthalpy measurements of liquid Fe-Ti alloys by levitation alloying calorimetry and calculation of the thermodynamic properties of mixing.[J] . ISIJ International,1995,35(12):1518 − 1522. doi: 10.2355/isijinternational.35.1518
[11]	FURUKAWA T, KATO E. Thermodynamics of binary liquid iron-titanium alloys by mass spectrometry[J] . Transactions of the Iron and Steel Institute of Japan,1976,16(7):382 − 387. doi: 10.2355/isijinternational1966.16.382
[12]	FRUEHAN R J. Activities in liquid Fe-AI-O and Fe-Ti-O alloys[J] . Metallurgical Transactions,1970,1:3403 − 3410.
[13]	GACHON J C, NOTIN M, HERTZ J. The enthalphy of mixing of the intermediate phases in the systems FeTi, CoTi, and NiTi by direct reaction calorimetry[J] . Thermochimica Acta,1981,48(1/2):155 − 164. doi: 10.1016/0040-6031(81)87031-1
[14]	DINSDALE A T, CHART T G, PUTLAND F H. Enthalpies of formation of binary phases in the Fe-Ni system[R]. National Physical Laboratory: Middlesex, 1985.
[15]	MURRAY J L. The Fe−Ti (iron-titanium) system[J] . Bulletin of Alloy Phase Diagrams,1981,2(3):320 − 334. doi: 10.1007/BF02868286
[16]	BOOKER P H. Ternary phase equilibria in the systems Ti-Fe-C, Ti-Co-C and Ti-Ni-c : Phase equilibria of the type metal carbonitride + graphite + nitrogen in the systems Ti-C-N, Zr-C-N, and Hf-C-N[EB/OL]. 1979.
[17]	VANTHYNE R J, KESSLER H D, HANSEN M. The systems titanium-chromium and titanium-iron[J] . Transactions of the American Society for Metals,1952,44:974 − 989.
[18]	HELLAWELL A. The constitution of manganese base alloys with metals of the second transition series[J] . Journal of the Less Common Metals,1959,1(5):343 − 347. doi: 10.1016/0022-5088(59)90036-0
[19]	MCQUILLAN A D. The application of hydrogen equilibriumpressure measurements to the investigation of titanium alloy systems[J] . Journal of the Japan Institute of Metals,1951(79):73 − 88.
[20]	MURAKAMI Y, KIMURA H, NISHIMURA Y. An investigation on the titanium-iron-carbon system (1st report). on the titanium-iron system[J] . Journal of the Japan Institute of Metals,1957,21(11):665 − 669.
[21]	KO M, NISHIZAWA T. Effect of magnetic transition on the solubility of alloying elements in alpha iron[J] . Journal of the Japan Institute of Metals,1979,43(2):118 − 126.
[22]	QIU C, JIN Z P. An experimental study and themodynamic evaluation of the Fe-Ti-W system at 1 000°C[J] . Scripta Metallurgica et Materialia,1993,28(1):85 − 90. doi: 10.1016/0956-716X(93)90542-Z
[23]	RAUB E, RAUB C J, RÖSCHEL E, et al. The α-Ti-Fe solid solution and its superconducting properties[J] . Journal of the Less Common Metals,1967,12(1):36 − 40. doi: 10.1016/0022-5088(67)90066-5
[24]	MATYKA J, FAUDOT F, BIGOT J. Study of iron solubility in α titanium[J] . Scripta Metallurgica,1979,13(7):645 − 648. doi: 10.1016/0036-9748(79)90126-1
[25]	BALESIUS A, GONSER U. Precision phase analysis[J] . Journal de Physique: Colloque,1976,37:C6 − 397.
[26]	STUPEL M M, BAMBERGER M, RON M. The solubility of iron in α-titanium in the temperature range 360~580 °C[J] . Journal of the Less Common Metals,1986,123(1/2):1 − 7. doi: 10.1016/0022-5088(86)90109-8
[27]	MOLL S, OGILVIE R. Solubility and diffusion of titanium in iron[J] . Transactions of AIME,1959,215:613 − 618.
[28]	FISCHER W, LORENTZ K, FABRITIUS H, et al. Investigation of phase transformations in iron alloys using a magnetic balance[J] . Arch Eisenhüttenwes,1966,37:78 − 87.
[29]	DUMITRESCU L, HILLERT M. Reassessment of the solubility of TiC and TiN in Fe[J] . Isij International,1999,39:84 − 90. doi: 10.2355/isijinternational.39.84
[30]	FENG Q, DUAN B, MAO L, et al. Thermodynamic assessment of Ti-Al-Fe-V quaternary system applied to novel titanium alloys designing[J] . Metals,2022,12(3):444. doi: 10.3390/met12030444
[31]	ZHANG G, ZHENG W, ZHAO Z, et al. Thermodynamic modeling of the Fe-Mn-Ti system[J] . Journal of Phase Equilibria and Diffusion,2021,42(3):363 − 372. doi: 10.1007/s11669-021-00889-7
[32]	WITUSIEWICZ V T, BONDAR A, HECHT U, et al. Experimental study and thermodynamic re-modelling of the constituent binaries and ternary B–Fe–Ti system[J] . Journal of Alloys and Compounds,2019,800:419 − 449. doi: 10.1016/j.jallcom.2019.05.341
[33]	HU T, ZENG Y, HUANG X M, et al. Experimental investigation of phase relationship in Ti–Fe-Hf ternary system[J] . Calphad,2019,67:101669. doi: 10.1016/j.calphad.2019.101669
[34]	CHEN Y, CHENG L, TANG B. Binary diffusion behaviour in Ti– X (X = Al, Mo, V, Cr, Fe) alloys[J] . International Journal of Materials Research,2018,109(6):569 − 572. doi: 10.3139/146.111642
[35]	LU X G, Selleby M, Sundman B. Implementation of a new model for pressure dependence of condensed phases in Thermo-Calc[J] . Calphad,2005,29(1):49 − 55. doi: 10.1016/j.calphad.2005.04.001