磁化史瓦西黑洞的有效势与稳定圆轨道

刘文芳; 周娜英; 张洪星; 孙鑫

doi:10.12299/jsues.22-0338

磁化史瓦西黑洞的有效势与稳定圆轨道

doi: 10.12299/jsues.22-0338

刘文芳^{1a, 1b,},
周娜英^{1a, 1b,},
张洪星^{1a, 1b},
孙鑫²

1a.
数理与统计学院
1b.
计算物理与应用研究中心, 上海 201620
2.
广西大学物理科学与工程技术学院, 南宁 530004

详细信息

作者简介:
刘文芳（1970−），女，实验师，本科，研究方向为天文科普与天体力学数值方法. E-mail：21200007@sues.edu.cn

中图分类号: P138
计量
- 文章访问数: 255
- HTML全文浏览量: 141
- PDF下载量: 40
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-11
- 刊出日期: 2023-09-30

Effective potential and stable circular orbits in magnetized Schwarzschild spacetime

LIU Wenfang^{1a, 1b
,},
ZHOU Naying^{1a, 1b
,},
ZHANG Hongxing^{1a, 1b},
SUN Xin²

1a.
School of Mathematics, Physics and Statistics
1b.
Center of Application and Research of Computational Physics, Shanghai University of Engineering Science, Shanghai 201620, China
2.
School of Physical Science and Technology, Guangxi University, Nanning 530004, China

摘要

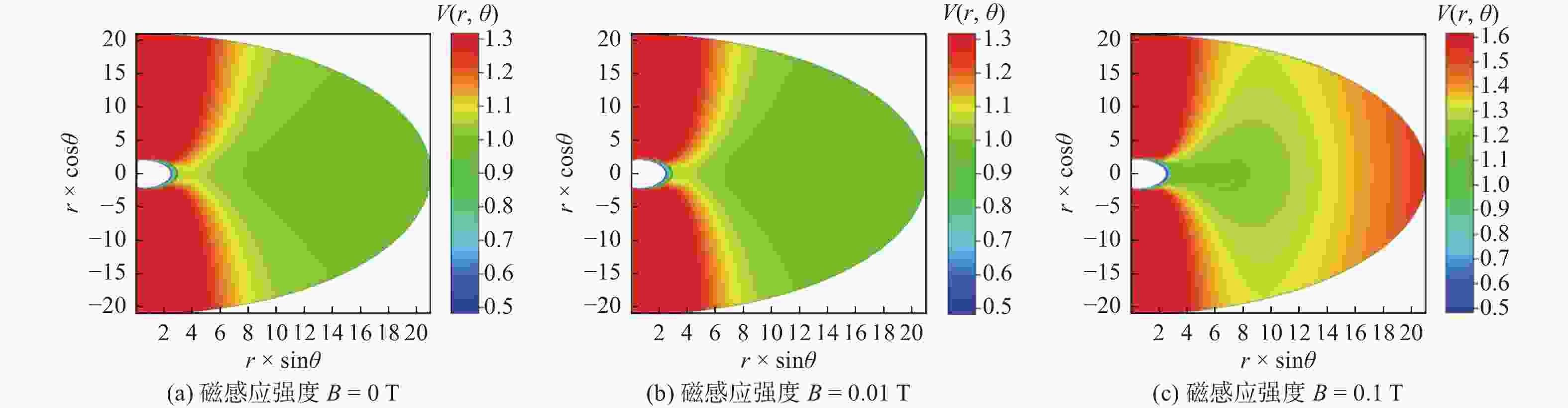
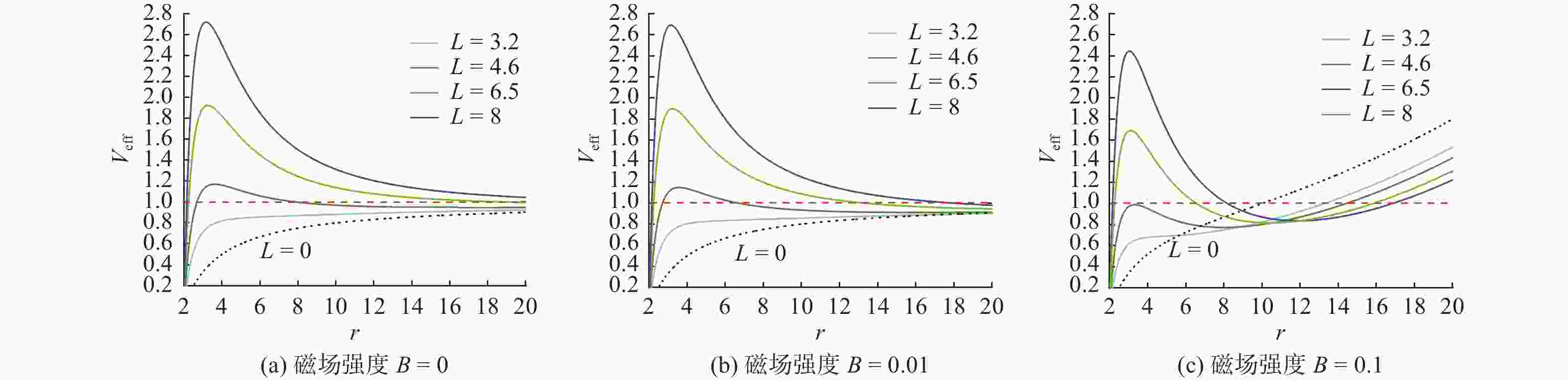
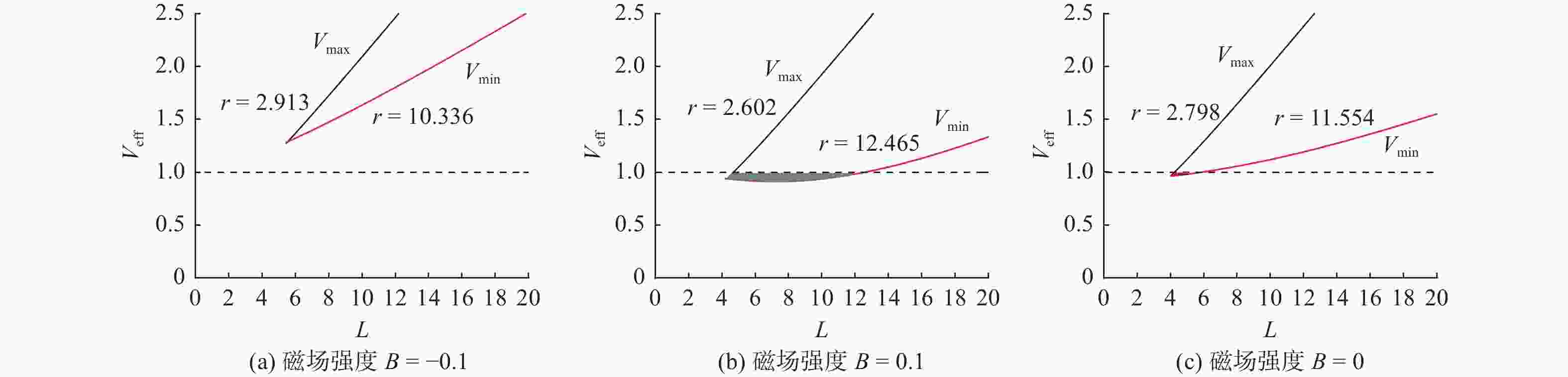
摘要: 利用赤道平面上的径向有效势研究带电粒子在有外部磁场的史瓦西黑洞附近的圆轨道运动，发现针对某特定的角动量和较小的外部磁场，稳定圆轨道很难存在；但随着磁感应强度的增大，稳定圆轨道容易形成，并且磁感应强度的增大会导致稳定圆轨道半径逐渐减小. 稳定圆轨道半径随着角动量的增大而逐渐增大. 角动量和径向距离函数曲线与径向距离和有效势在讨论圆轨道性质上具有同等效果.
- 黑洞 /
- 磁场 /
- 有效势 /
- 稳定圆轨道
Abstract: An effective potential in the equatorial plane was used to study the circular motion of charged particles near the Schwarzschild black hole immersed into an external magnetic field. It is found that no stable circular orbits exist for some angular momenta and small magnetic fields. However, the stable circular orbit easily occurs and has small radius when the magnetic induction increases. The radius of stable circular orbit increases with an increase of the angular momentum. The relation between the angular momentum and a radial distance can show the features of circular orbits, as the relation between the effective potential and the radial distance can.
- black hole /
- magnetic field /
- effective potential /
- stable circular orbits

HTML全文

图 1 3个不同磁感应强度的有效势分布

Figure 1. Effective potential distribution of three different magnetic induction

下载: 全尺寸图片幻灯片

图 2 2维有效势能级分布

Figure 2. 2D effective potential energy level distribution

下载: 全尺寸图片幻灯片

图 3 不同的磁感应强度下，有效势随着试验粒子角动量变化的分布

Figure 3. Distribution of effective potential with angular momentum of the test particle under different magnetic induction

下载: 全尺寸图片幻灯片

图 4 与有效势对应的角动量L与轨道半径r的函数关系曲线

Figure 4. Functional relationship curve between angular momentum L and orbital radius r corresponding to effective potential

下载: 全尺寸图片幻灯片

图 5 在不同能量和磁感应强度情况下的角动量L与轨道半径r的函数关系曲线

Figure 5. Functional relation curve of angular momentum L and orbital radius r under different energy and magnetic field intensity

下载: 全尺寸图片幻灯片

图 6 不稳定圆轨道对应的有效势$ {V}_{{\rm{max}}} $和稳定圆轨道对应的有效势$ {V}_{{\rm{min}}} $与$ L $的函数关系

Figure 6. Functional relationship between effective potential $ {V}_{{\rm{min}}} $ corresponding to unstable circular orbits and effective potential $ {V}_{{\rm{max}}} $ corresponding to stable circular orbits and $ L $

下载: 全尺寸图片幻灯片

表 1 与图1对应的圆轨道半径r值

Table 1. Radii r of circular orbit corresponding to Fig.1

磁感应强度	r	$ E^{2}\left(V_{\text {eff }}\right) $	$V_{\text {eff } }^{\prime \prime}$	稳定性
B=0	3.618937	1.170126	−0.162335	不稳定
B=0	17.541063	0.946911	0.000294	稳定
B=0.01	3.577530	1.149839	−0.174817	不稳定
B=0.01	16.351999	0.912641	0.000519	稳定
B=0.1	3.313035	0.988926	−0.272909	不稳定
B=0.1	7.986825	0.772967	0.016335	稳定

下载: 导出CSV

表 2 与图3对应的圆轨道半径r值

Table 2. Radii r of circular orbit corresponding to Fig.3

磁感应强度	L=6.5				L=8
磁感应强度	r	$ E^{2}\left(V_{\text {eff }}\right) $	$V_{\text {eff } }^{\prime \prime}$	稳定性	r	$ E^{2}\left(V_{\text {eff }}\right) $	$V_{\text {eff } }^{\prime \prime}$	稳定性
B=0	3.250000	1.923077	−0.640874	不稳定	3.155590	2.719855	−1.163588	不稳定
B=0	39.000000	0.975071	0.000030	稳定	60.844410	0.983849	0.000008	稳定
B=0.01	3.231197	1.898294	−0.664131	不稳定	3.141993	2.690759	−1.194549	不稳定
B=0.01	26.817870	0.936274	0.000273	稳定	32.780111	0.945019	0.000238	稳定
B=0.1	3.090400	1.692793	−0.860438	不稳定	3.035547	2.445489	−1.460505	不稳定
B=0.1	10.398772	0.816597	0.017095	稳定	11.870141	0.836892	0.017346	稳定

下载: 导出CSV

表 3 不同磁感应强度影响下最内稳定圆轨道半径(r_ISCO)、最内稳定圆轨道角动量(L_ISCO)及E²的值

Table 3. Values of r_ISCO, L_ISCO and value E² under influence of different magnetic field intensities

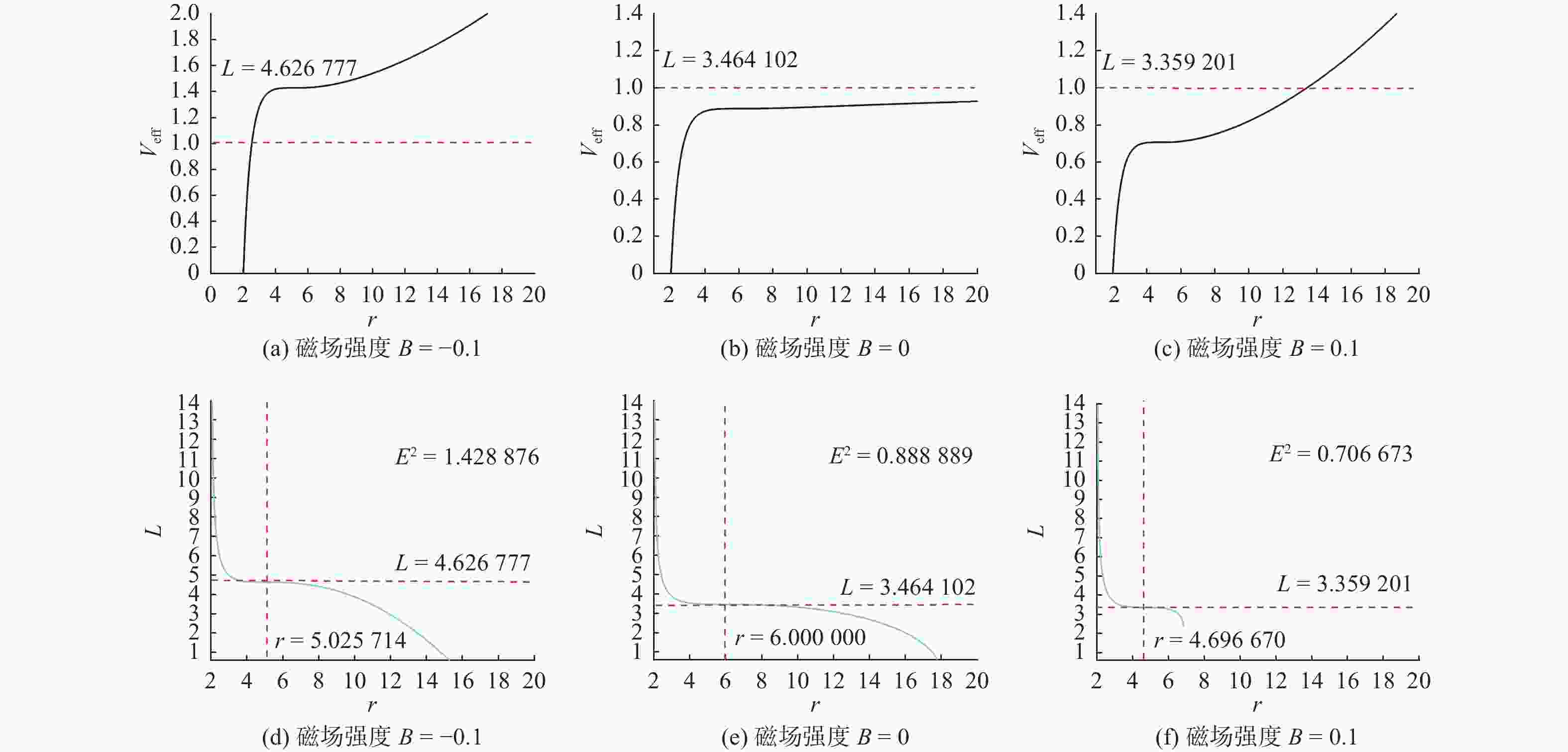
参数	${\mathit{r} }_{{\rm{ISCO}} }$	${\mathit{L} }_{\rm{ISCO} }$	$ {\mathit{E}}^{2} $	${ {L}_{{\rm{ISCO}}} }^{\prime \prime}$
B=−0.1	5.025714	4.626777	1.428876	−4.560000×10⁻⁸
B=0	6.000000	3.464102	0.888889	−3.608436×10⁻⁸
B=0.1	4.696670	3.359201	0.706673	−6.101820×10⁻⁷

下载: 导出CSV

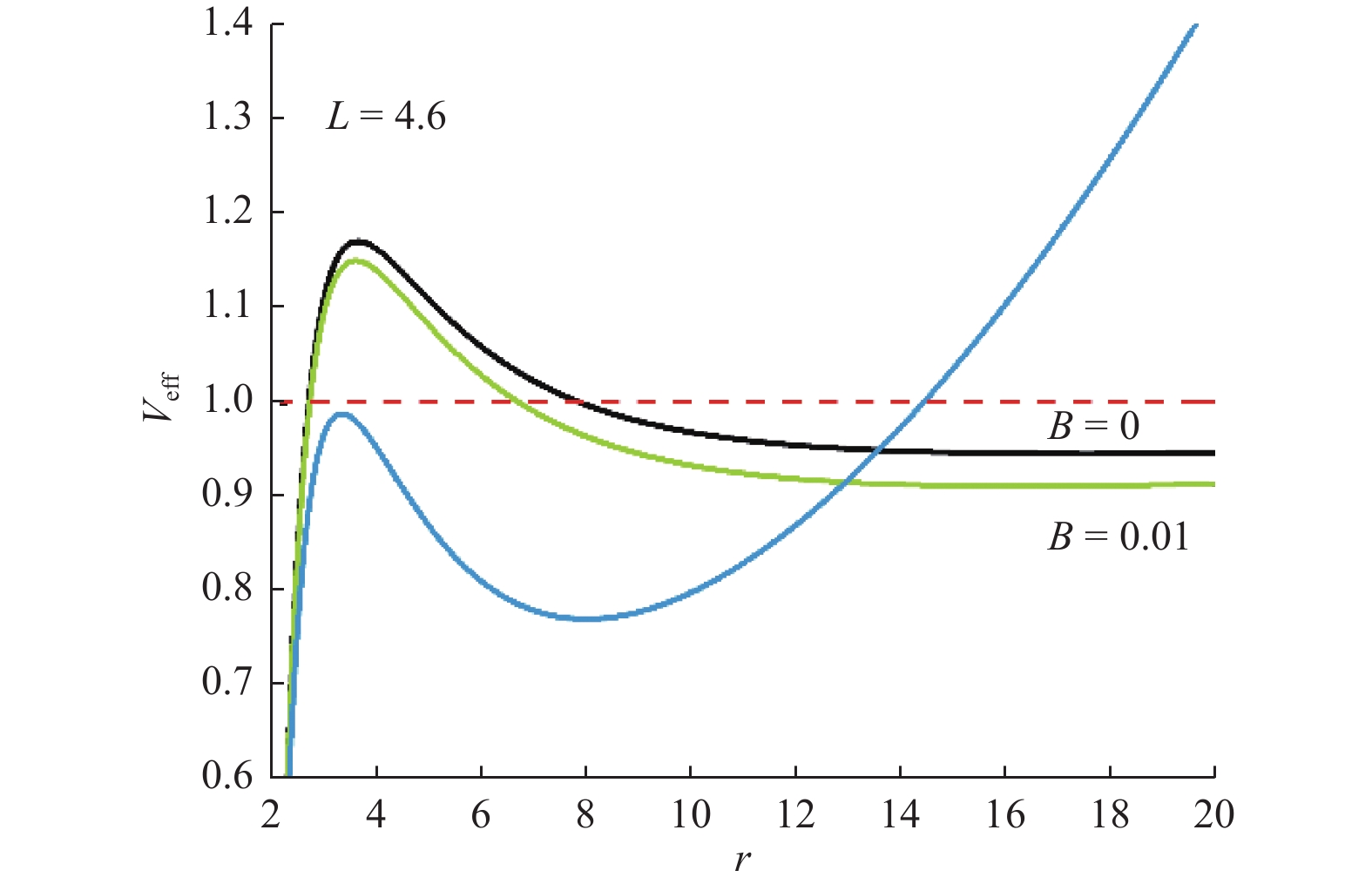
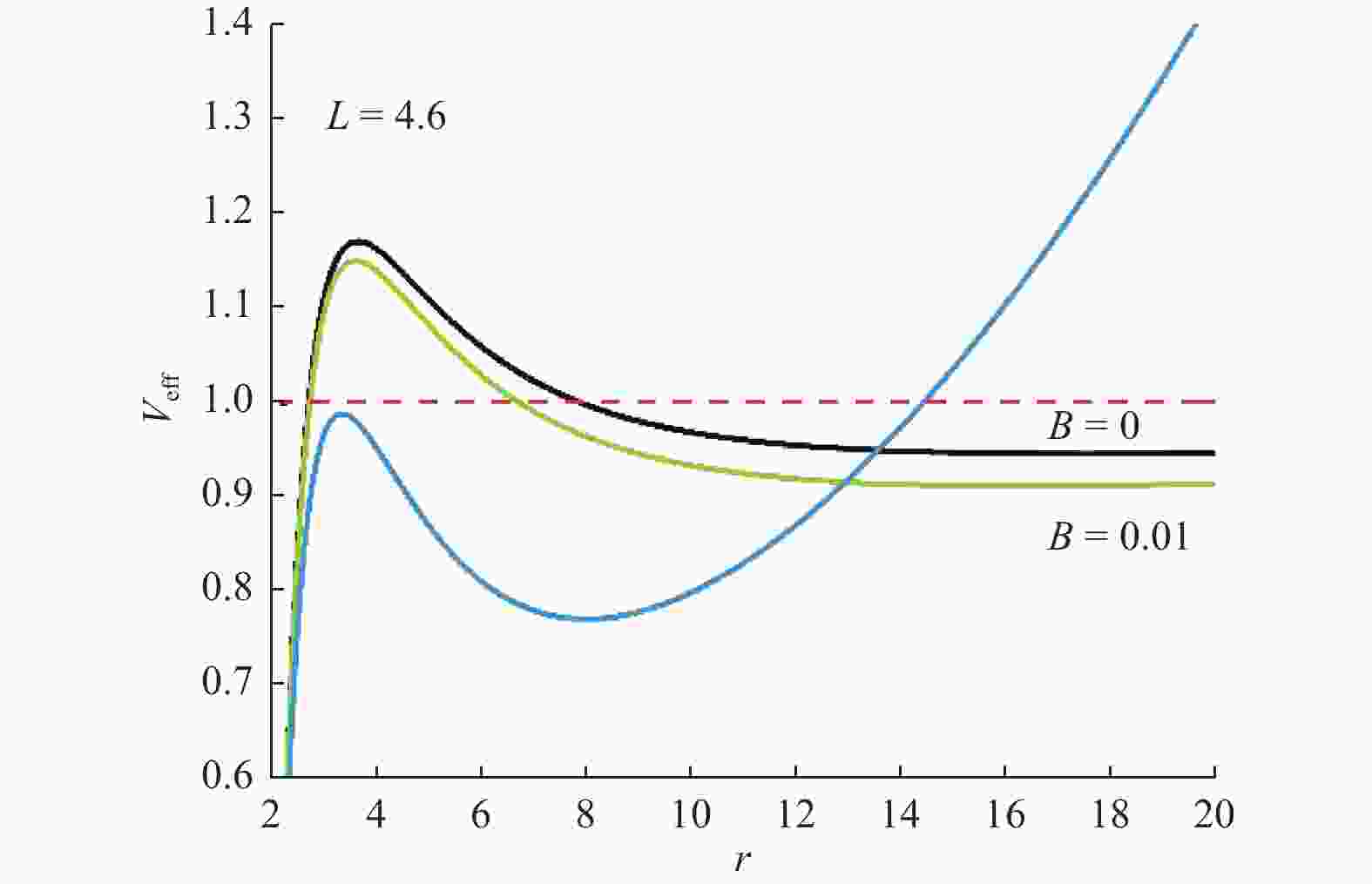
表 4 角动量$L=4.6$不同磁感应强度影响下$ { r} $及$ {E}^{2} $值

Table 4. values of$ r $ and $ {E}^{2} $under influences of different magnetic induction with angular momentum $ L=4.6 $

参数	r	$ {\mathit{E}}^{2} $
B=0	3.618937	1.170126
B=0	17.541063	0.946911
B=0.01	3.577530	1.149839
B=0.01	16.351999	0.912641
B=0.1	3.313035	0.988926
B=0.1	7.986825	0.772967

下载: 导出CSV

表 5 不同磁感应强度下$ r$、$ {E}^{2} $及对应$ L $值

Table 5. $ r $, $ {E}^{2} $ and corresponding $ L $ under different magnetic induction

参数	r	$ \mathit{L} $	$ {\mathit{L}}^{\prime \prime} $	稳定性
B=0, $ {\mathit{E}}^{2}=0.946911 $	4.295401	3.773997	0.151900	不稳定
B=0, $ {\mathit{E}}^{2}=0.946911 $	17.541063	4.599999	−0.011102	稳定
B=0.01, $ {\mathit{E}}^{2}=0.942903 $	4.295814	3.706091	0.152276	不稳定
B=0.01, $ {\mathit{E}}^{2}=0.942903 $	16.351999	4.599998	−0.024210	稳定
B=0.1, $ {\mathit{E}}^{2}=0.772967 $	3.705074	3.740838	0.389130	不稳定
B=0.1, $ {\mathit{E}}^{2}=0.772967 $	7.986825	4.599998	−0.492759	稳定

下载: 导出CSV

参考文献(27)

[1]	EINSTEIN A. Sitzungsberichte der köiglich preuschen $ \beta $ akademie der wissenschaften [M]. Berlin: Deutsche Akademie der Wissenschaften zu Berlin, 1915: 425.
[2]	EINSTEIN A, SITZUNGSBER K. Eine neue formale deutung der maxwellschen feldgleichungen der elektrodynamik [M]. New York: Sons John Wiley and Sons, 1916: 688.
[3]	EATOUGH R P, FALCKE H, KARUPPUSAMY R. A strong magnetic field around the supermassive black hole at the centre of the Galaxy[J] . Nature,2013,501:391 − 394. doi: 10.1038/nature12499
[4]	ZHANG H X, ZHOU N Y, LIU W F, et al. Charged particle motions near non-Schwarzschild black holes with external magnetic fields in modified theories of gravity[J] . Universe,2021,7(12):488. doi: 10.3390/universe7120488
[5]	SUN W, WANG Y, LIU F Y, et al. Applying explicit symplectic integrator to study chaos of charged particles around magnetized Kerr black hole[J] . European Physical Journal C,2021,81:785.
[6]	LI D, WANG Y, DENG C, et al. Coherent post-Newtonian Lagrangian equations of motion[J] . European Physical Journal Plus,2020,135:390. doi: 10.1140/epjp/s13360-020-00407-7
[7]	WU X, ZHANG H. Chaotic dynamics in a superposed Weyl spacetime[J] . The Astrophysical Journal,2006,652(2):1466. doi: 10.1086/508129
[8]	WANG Y, SUN W, LIU F Y, et al. Construction of explicit symplectic integrators in general relativity. I. Schwarzschild black holes[J] . The Astrophysical Journal,2021,907(2):66. doi: 10.3847/1538-4357/abcb8d
[9]	WANG Y, SUN W, LIU F Y, et al. Construction of explicit symplectic integrators in general relativity. III. Reissner–Nordström-(anti)-de sitter black holes[J] . The Astrophysical Journal Supplement Series,2021,254(1):8. doi: 10.3847/1538-4365/abf116
[10]	WU X, WANG Y, SUN W, et al. Construction of explicit symplectic integrators in general relativity. IV. Kerr black holes[J] . The Astrophysical Journal,2021,914(1):63. doi: 10.3847/1538-4357/abfc45
[11]	ZHOU N Y, ZHANG H X, LIU W F, et al. A note on the construction of explicit symplectic integrators for Schwarzschild spacetimes[J] . The Astrophysical Journal,2022,927(2):160. doi: 10.3847/1538-4357/ac497f
[12]	YANG D Q, CAO W F, ZHOU N Y, et al. Chaos in a magnetized modified gravity Schwarzschild spacetime[J] . Universe,2022,8(6):320. doi: 10.3390/universe8060320
[13]	HU A R, HANG G Q. Dynamics of charged particles in the magnetized γ spacetime[J] . European Physical Journal Plus,2021,136:1210. doi: 10.1140/epjp/s13360-021-02194-1
[14]	SUN X, WU X, WANG Y, et al. Dynamics of charged particles moving around Kerr black hole with inductive charge and external magnetic field[J] . Universe,2021,7:410. doi: 10.3390/universe7110410
[15]	YI M, WU X. Dynamics of charged particles around a magnetically deformed Schwarzschild black hole[J] . Physica Scripta,2020,95:085008. doi: 10.1088/1402-4896/aba4c2
[16]	NARAYAN R, JOHNSON M D, GAMMIE C F. The shadow of a spherically accreting black hole[J] . The Astrophysical Journal Letters,2019,885:L33. doi: 10.3847/2041-8213/ab518c
[17]	GRALLA S E, HOLZ D E, WALD R M. Black hole shadows, photon rings, and lensing rings[J] . Physical Review D,2019,100:024018. doi: 10.1103/PhysRevD.100.024018
[18]	PENG J, GUO M Y, FENG X H. Influence of quantum correction on the black hole shadows, photon rings and lensing rings[J] . Chinese Physics C,2021,45:085103.
[19]	HU S Y, DENG C, LI D, et al. Observational signatures of Schwarzschild-MOG black holes in scalar -tensor -vector gravity: shadows and rings with different accretions[J] . European Physical Journal C,2022,82:885. doi: 10.1140/epjc/s10052-022-10868-y
[20]	ZHANG H X, ZHOU N Y, LIU W F, et al. Equivalence between two charged black holes in dynamics of orbits outside the event horizons[J] . General Relativity and Gravitation,2022,54:110. doi: 10.1007/s10714-022-02998-1
[21]	CAO W F, LIU W F, WU X. Integrability of Kerr-Newman spacetime with cloud strings, quintessence and electromagnetic field[J] . Physical Review D,2022,105:124039. doi: 10.1103/PhysRevD.105.124039
[22]	KOVÁŘ J, SLANÝ P, CREMASCHINI C, et al. Electrically charged matter in rigid rotation around magnetized black hole[J] . Physical Review D,2014,90:044029. doi: 10.1103/PhysRevD.90.044029
[23]	HAWLEY J F, BALBUS S A. A powerful local shear instability in weakly magnetized disks. I-Linear analysis. II-Nonlinear evolution[J] . The Astrophysical Journal,1991,376:223. doi: 10.1086/170271
[24]	CAEMASCHINI C, STUCHLÍK Z. Magnetic loop generation by collisionless gravitationally bound plasmas in axisymmetric tori[J] . Physical Review E,2013,87:043113. doi: 10.1103/PhysRevE.87.043113
[25]	KOLOŠ. Quasi-harmonic oscillatory motion of charged particles around a Schwarzschild black hole immersed in a uniform magnetic field[J] . Classical Quantum Gravity,2015,32:165009. doi: 10.1088/0264-9381/32/16/165009
[26]	WANG Y, SUN W, LIU F Y, et al. Construction of explicit symplectic integrators in general relativity. II. Reissner–Nordström black holes[J] . The Astrophysical Journal,2021,909(1):22. doi: 10.3847/1538-4357/abd701
[27]	Wald R M. General Relativity [M]. Chicago: University of Chicago Press, 1984: 317.