Capacitance status identification of subway vehicles based on optimized VMD and energy relative entropy
-
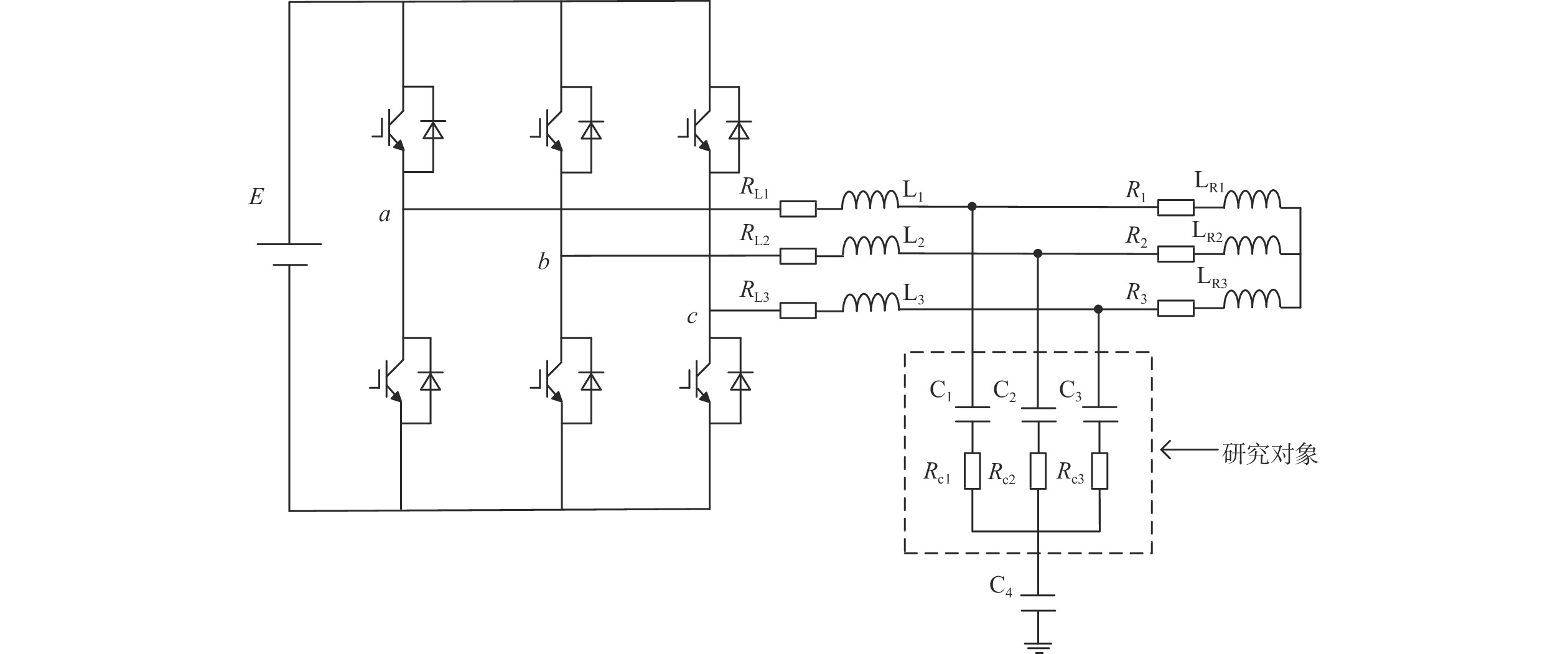
摘要: 针对地铁车载电容性能退化无明显征兆这一现状，提出一种基于优化变分模态分解(variational mode decomposition, VMD)和能量相对熵的电容状态识别方法。通过Matlab仿真建模，提取电容在正常状态和不同退化情况下负载侧输出电压信号并利用优化VMD进行分解得到若干模态分量。将其作为特征样本，对上述各状态的本征模态分量的能量特征向量进行相对熵分析，得到电容退化识别阈值。实际应用时，将待测电路的能量相对熵值与识别阈值进行比较从而完成电容状态识别。分析结果表明，此方法简单有效，判断正确率为93.3%。Abstract: Aiming at the problem that there is no obvious symptom of capacitance performance degradation on subway vehicles, a capacitance status identification method based on optimized variational mode decomposition (VMD) and energy relative entropy was proposed. By establishing a Matlab circuit model, the output voltage signals of the capacitance at normal status or different degradation conditions were extracted, then the characteristic samples were obtained by decomposition of optimized VMD. And the relative entropy analysis of the energy eigenvectors of the eigenmode components at the above status was carried out to obtain the identification threshold of capacitance degradation. In practical application, the relative entropy value of the energy of the circuit under test and the normal status was compared with the identification threshold to complete the capacitance status identification. The analysis result shows that this method can identify the capacitance status simply and effectively, and the accuracy is 93.3%.
-
图 3 电容3种状态下电路信号的VMD分解结果及频谱图
Figure 3. Results of VMD decomposition and spectrum diagram of circuit signal in three states of capacitance
表 1 故障模式表
Table 1. Failure mode table
故障模式 C/μF ESR值/Ω c退化程度/％ f0(正常状态) 78 0.2 0 f1 76.44 0.22 2 f2 74.88 0.24 4 f3 73.32 0.26 6 f4 71.76 0.28 8 f5 70.2 0.3 10 f6 68.64 0.32 12 f7 67.08 0.34 14 f8 65.52 0.36 16 f9 63.96 0.38 18 f10 62.4 0.4 20 f11 60.84 0.42 22 f12 59.28 0.44 24 f13 57.72 0.46 26 f14 56.16 0.48 28 f15 54.6 0.5 30 
下载: 导出CSV
表 2 不同k值下分量能量和的差值η
Table 2. Difference η of component energy sum for different values of k
预设分解数k 正常状态η 软故障η 硬故障η 3 0.0107 0.0167 0.0203 4 0.0071 0.0085 0.0100 5 0.0031 0.0046 0.0059 6 0.0008 0.0052 0.0066 7 0.0038 0.0023 0.0030 8 0.0016 0.0011 0.0011
下载: 导出CSV
表 3 三相电压信号特征参数值
Table 3. Three-phase voltage signal characteristic parameter values
信号位置 IMF1能量值 IMF2能量值 IMF3能量值 f0 a相 399.8052 5.3112 4.0059 f0 b相 402.0965 5.8990 4.1760 f0 c相 400.5862 5.9049 4.1193 f6 a相 417.0651 7.3981 6.0358 f6 b相 393.7950 5.9154 4.1874 f6 c相 393.9093 5.9235 7.8144 f11a相 432.6332 9.3866 2.1068 f11 b相 387.4031 5.9297 4.1996 f11 c相 387.9112 5.9166 4.1930
下载: 导出CSV
表 4 故障阈值
Table 4. Failure threshold
电路状态 能量相对熵值 正常 (0 ~ 0.0305) 软故障 [0.0305 ~ 0.0564) 失效状态 [0.0564 ~ ∞)
下载: 导出CSV
表 5 状态识别汇总表
Table 5. State identification summary table
实际电路状态 能量相对熵值Q 结果 正常1 0.0055 符合 正常2 0.0099 符合 正常3 0.0153 符合 正常4 0.0207 符合 正常5 0.0252 符合 软故障1 0.0293 不符合 软故障2 0.0365 符合 软故障3 0.0399 符合 软故障4 0.0466 符合 软故障5 0.0495 符合 失效状态1 0.0571 符合 失效状态2 0.0616 符合 失效状态3 0.0681 符合 失效状态4 0.0720 符合 失效状态5 0.0778 符合 正确率/％ 93.3
下载: 导出CSV
-
[1] 雷登云, 段孝星, 王力纬, 等. BUCK电源模块输出电容ESR在线检测电路设计[J] . 电子产品可靠性与环境试验,2019,37(2):26 − 30. [2] 孟金磊, 陈旭. 基于状态观测器的电解电容在线状态监测方法[J] . 电力电子技术,2018,52(8):59 − 62. [3] 朱城昊, 王晗, 高少亭, 等. 风电变流器DC-Link电容器准在线状态监测方法[J] . 高电压技术,2023,49(1):373 − 382. [4] 俞珊, 徐志望, 董纪清. 开关电源中电解电容寿命预测分析[J] . 电源学报,2016,14(6):87 − 92, 121. [5] 沈茜, 任磊, 龚春英, 等. 一种基于系统辨识的Buck型变换器特征参数提取方法[J] . 中国电机工程学报,2016,36(20):5624 − 5631. [6] 姜媛媛, 陈李, 魏念巍. 基于时域特征DC_DC电路软故障诊断[J] . 新余学院学报,2020,25(2):11 − 18. [7] 陈李. 变工况Buck电路软故障特征提取方法研究 [D]. 淮南: 安徽理工大学 2020. [8] 姜媛媛. 电力电子电路故障诊断及预测关键技术研究 [D]. 南京: 南京航空航天大学 2018. [9] 吴小涛, 严世伦. 基于相关性的最优变分模态分解算法[J] . 黄冈师范学院学报,2019,39(3):6 − 10. [10] 邓思成, 宋玉琴. 优化VMD在轴承故障诊断中的应用[J] . 科学技术创新,2019(6):16 − 18. [11] 宋玉琴, 邓思成, 路彦刚. K值优化的VMD在轴承故障诊断中的应用[J] . 测控技术,2019,38(4):117 − 121. [12] 陈剑, 夏康, 黄凯旋, 等. 基于VMD相对能量熵和自适应ARMA模型的轴承性能退化趋势动态预警[J] . 电子测量与仪器学报,2020,34(8):116 − 123. [13] 徐艳春, 赵彩彩, 孙思涵, 等. 基于改进LMD和能量相对熵的主动配电网故障定位方法[J] . 中国电力,2021,54(11):133 − 143. -
下载:
点击查看大图
计量
- 文章访问数: 212
- HTML全文浏览量: 63
- PDF下载量: 326
- 被引次数: 0
