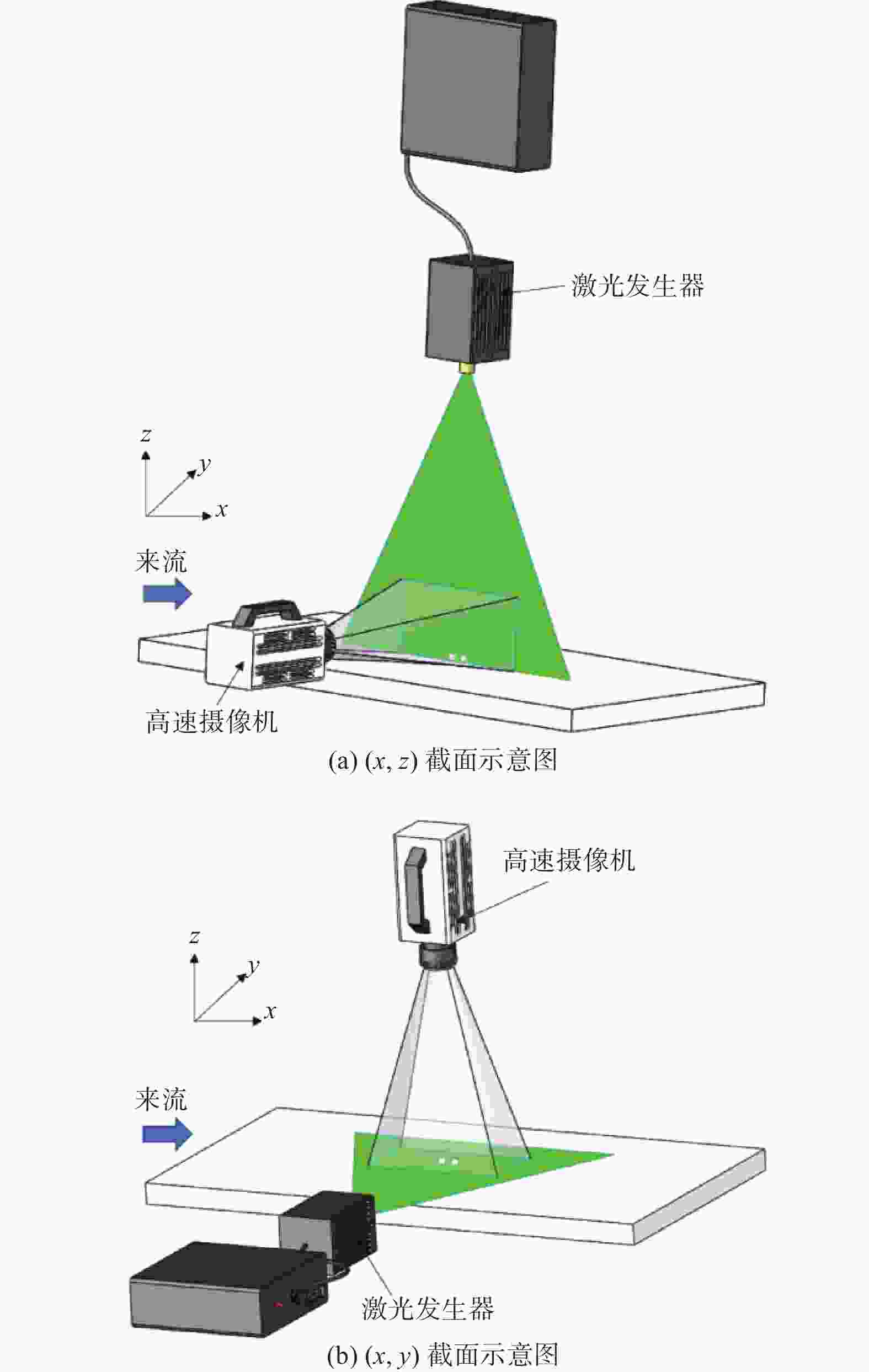
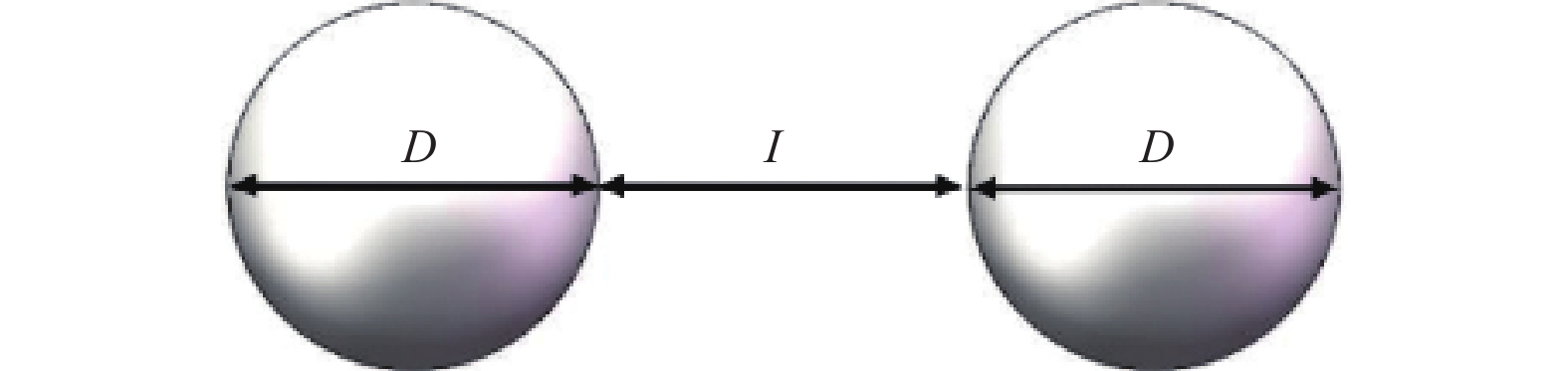
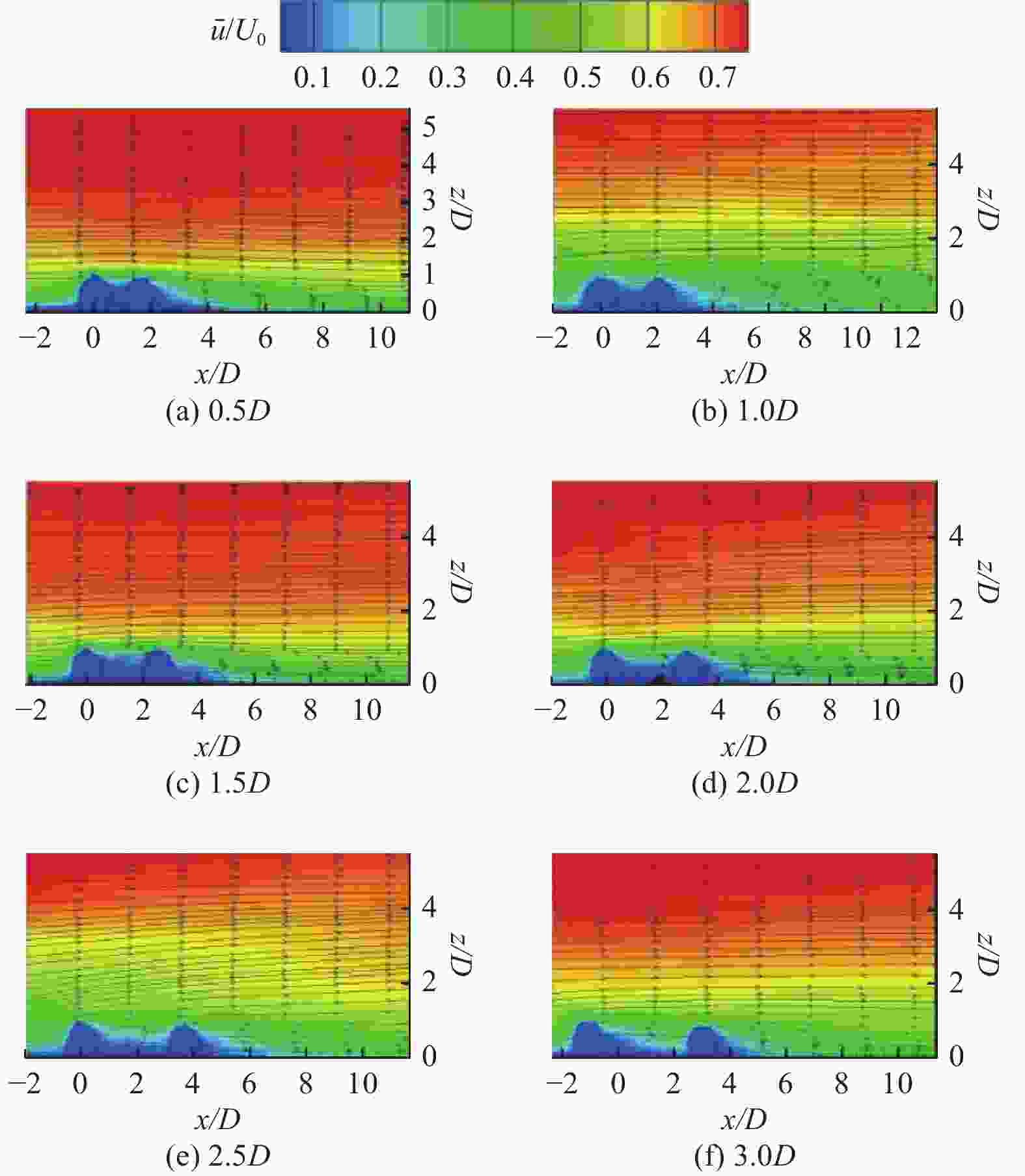
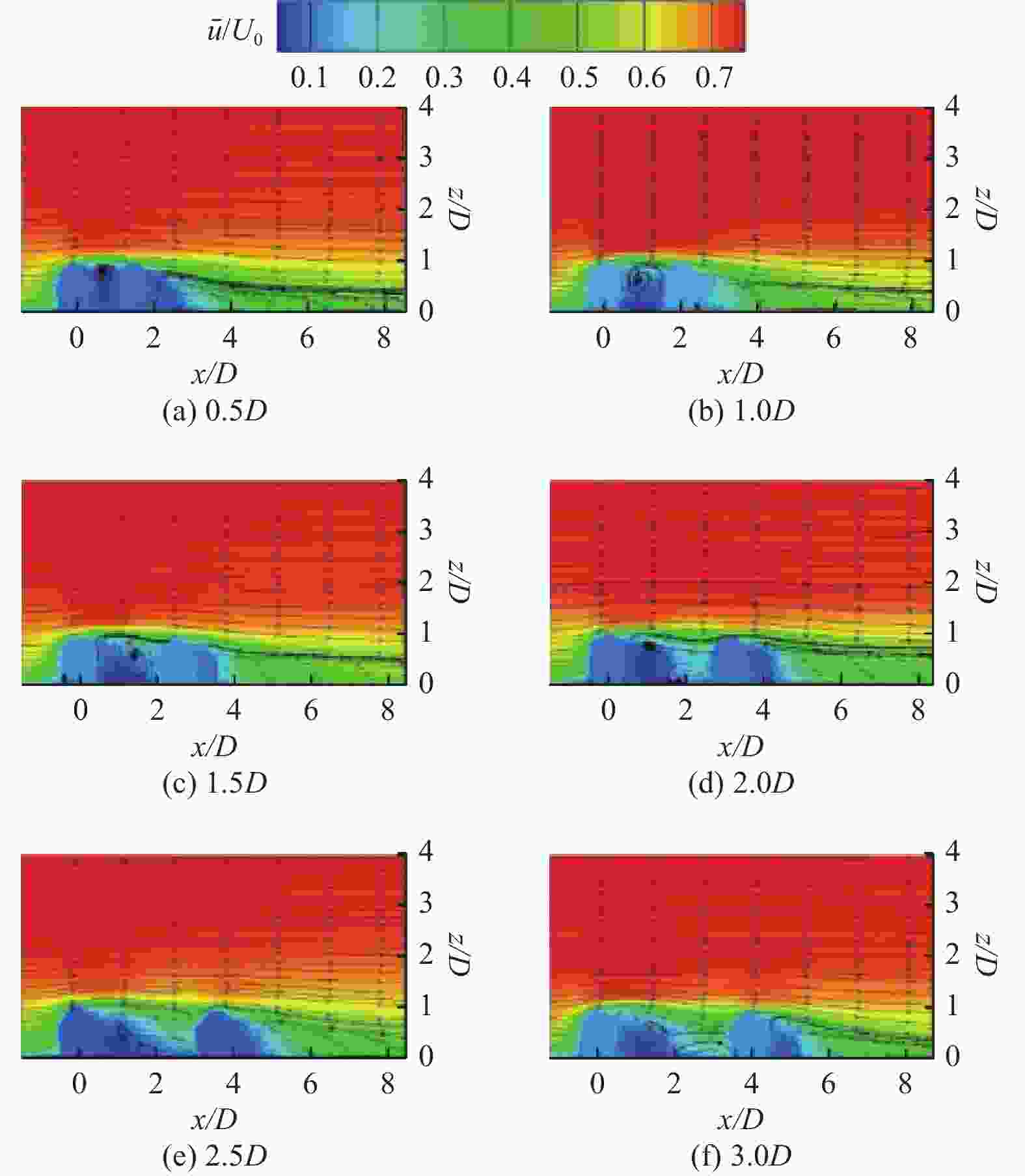
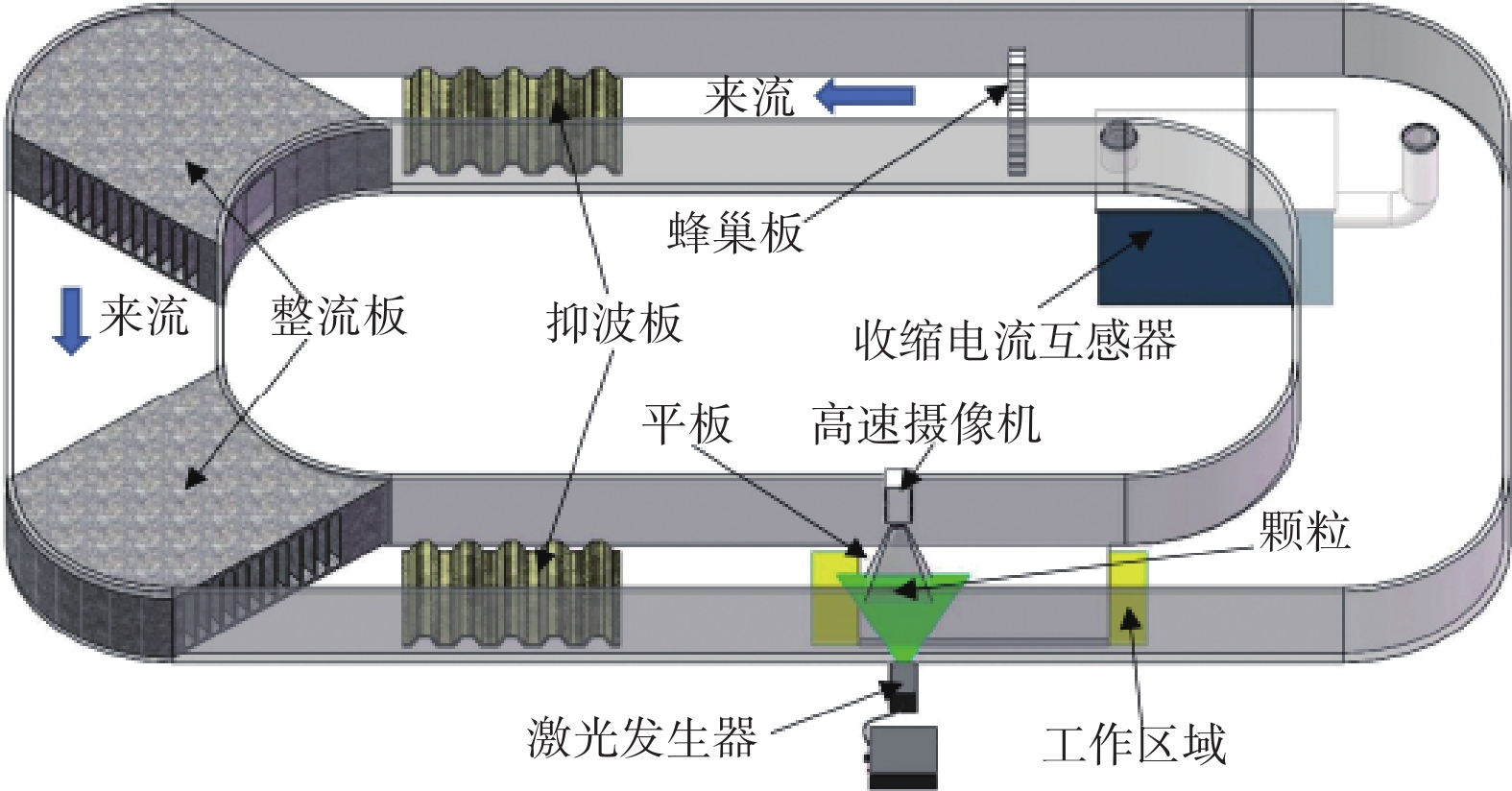
Effect of two-sphere particles on flow field structure of flat plate boundary layer
-
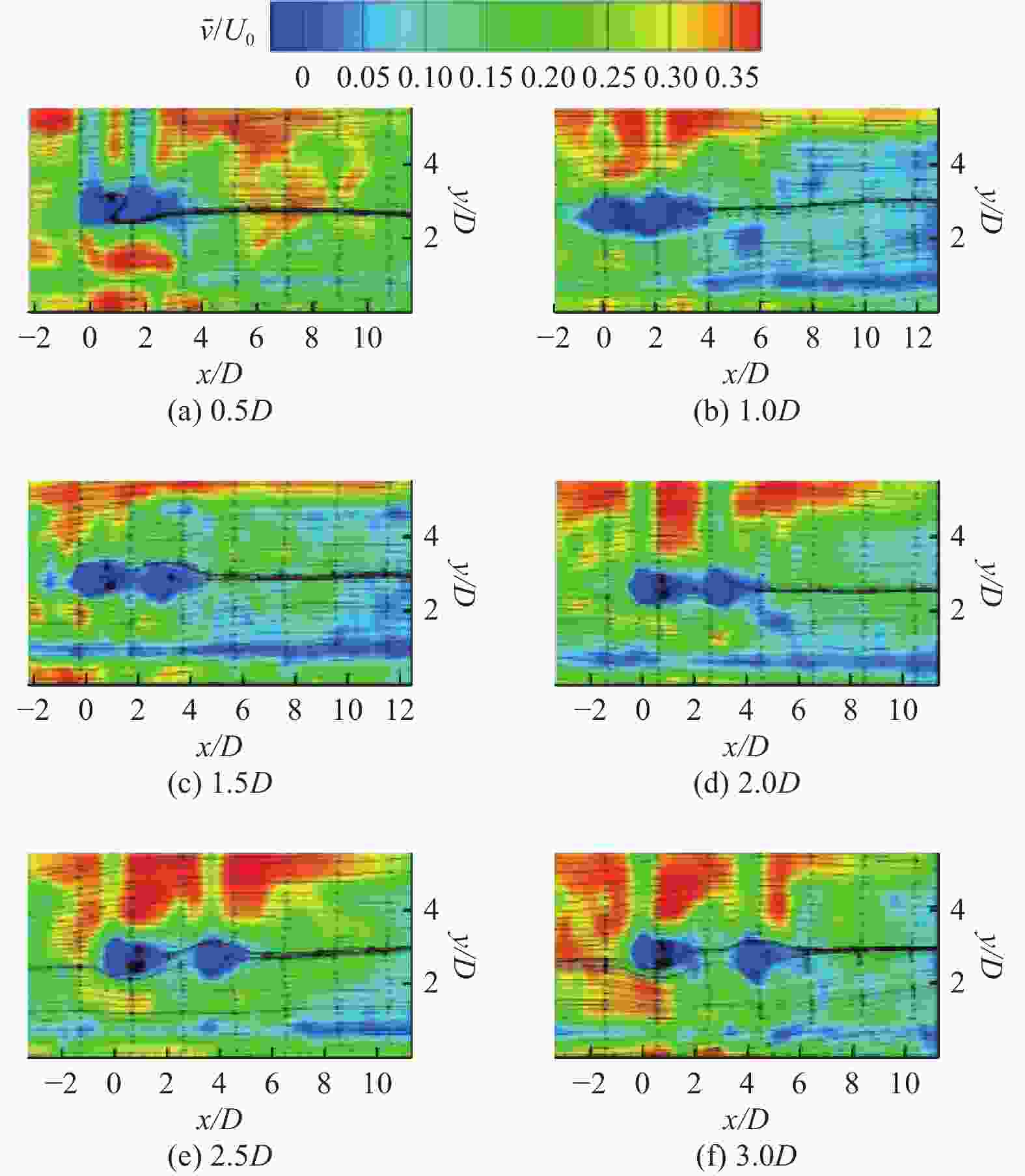
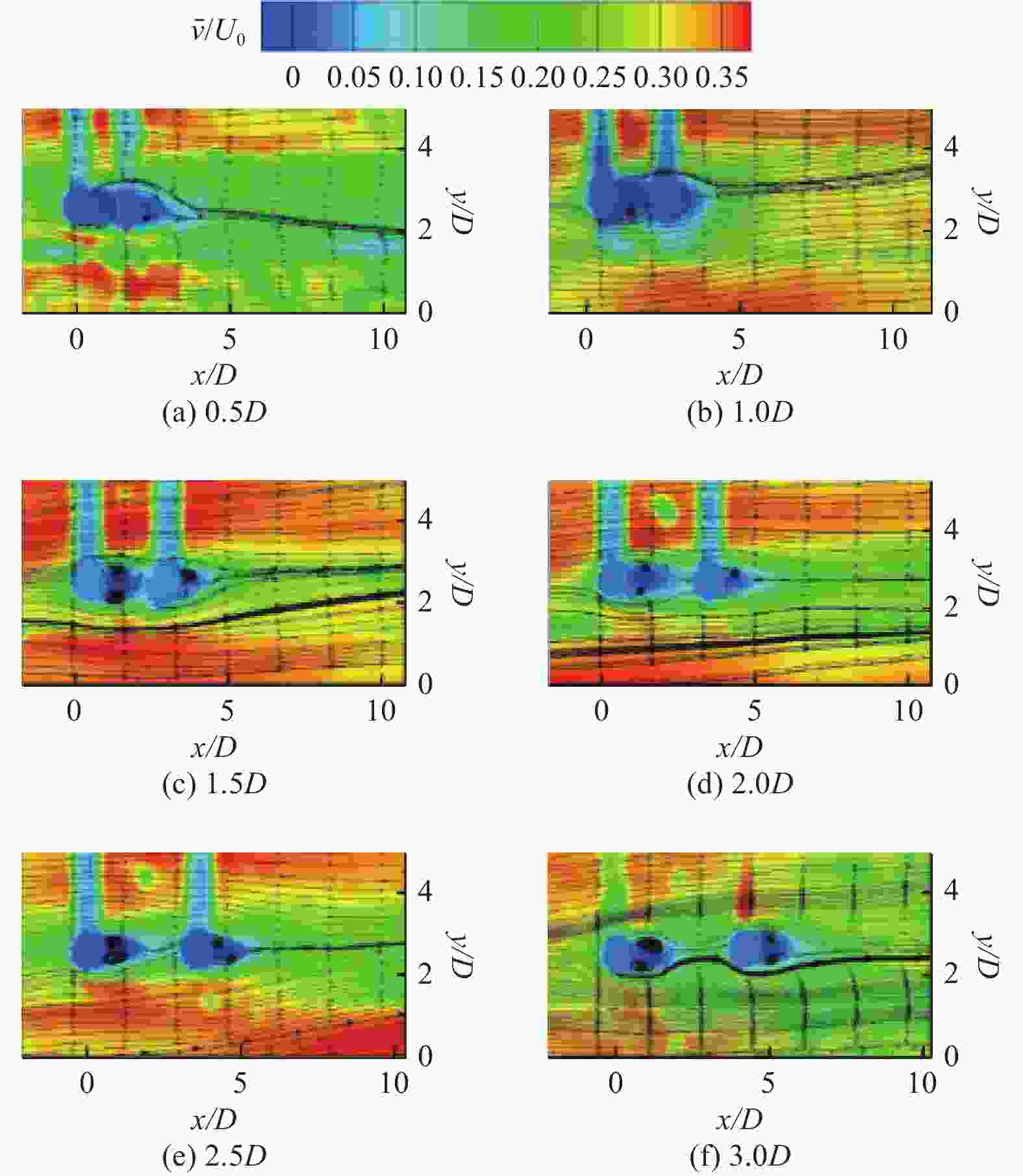
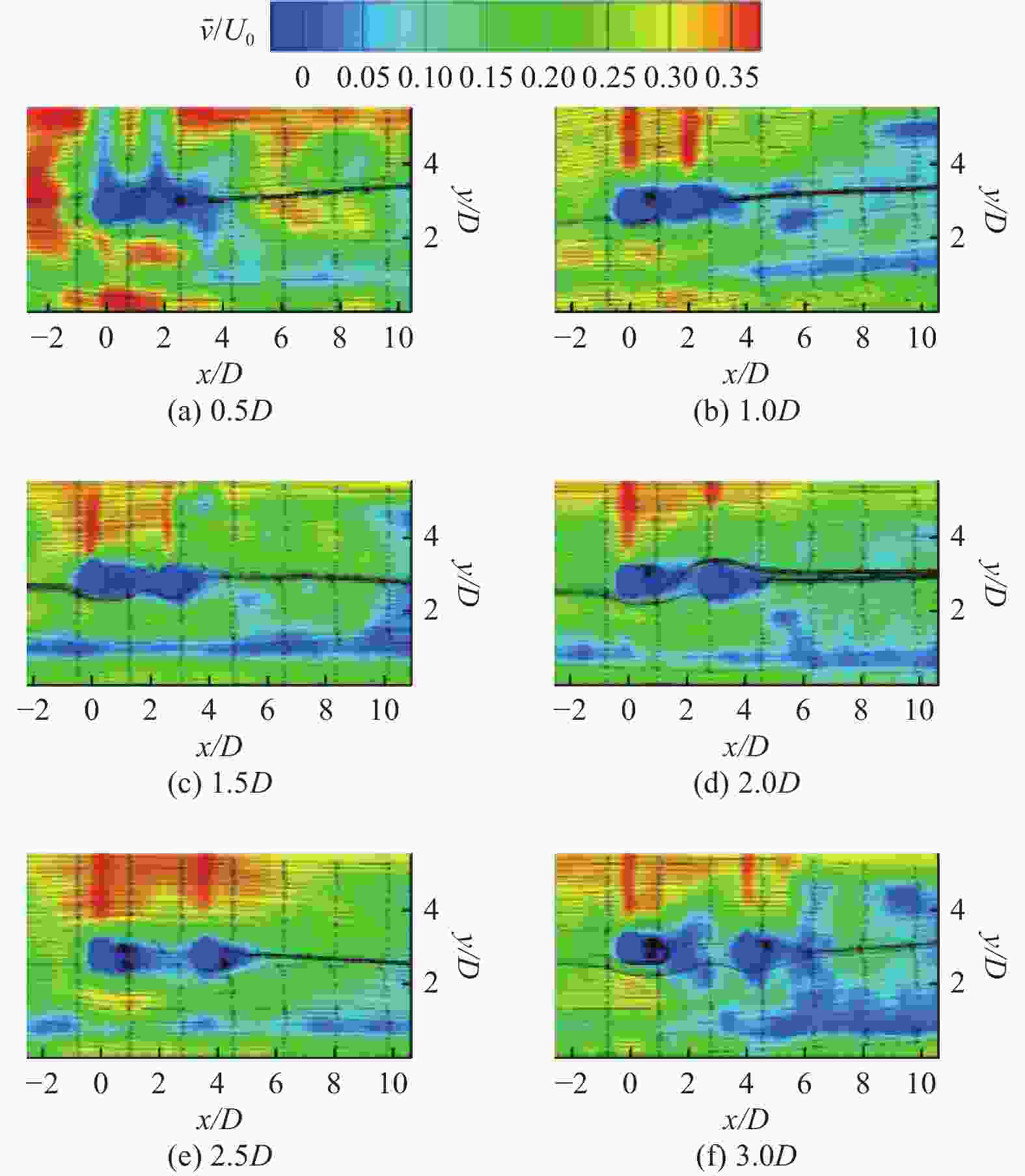
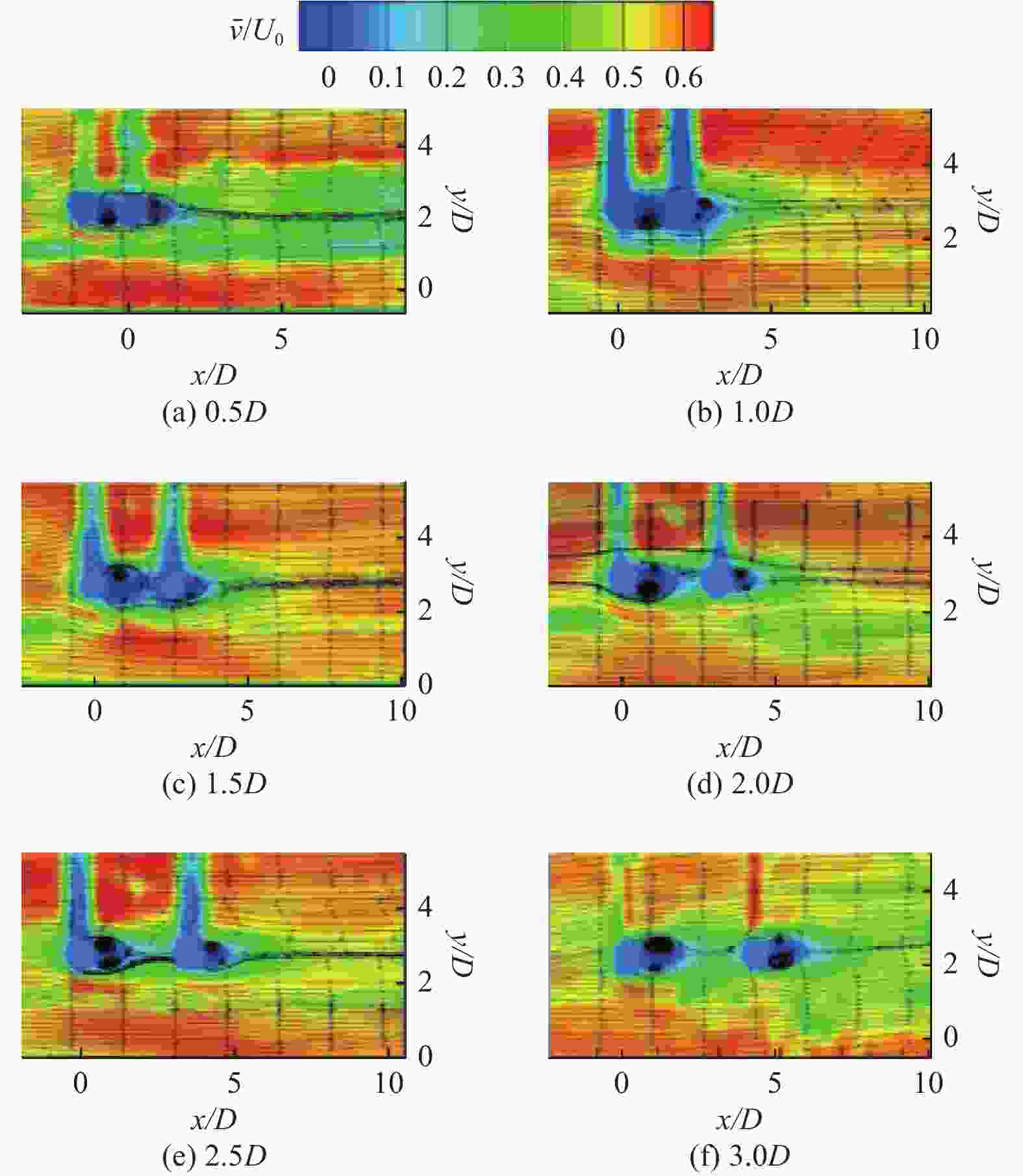
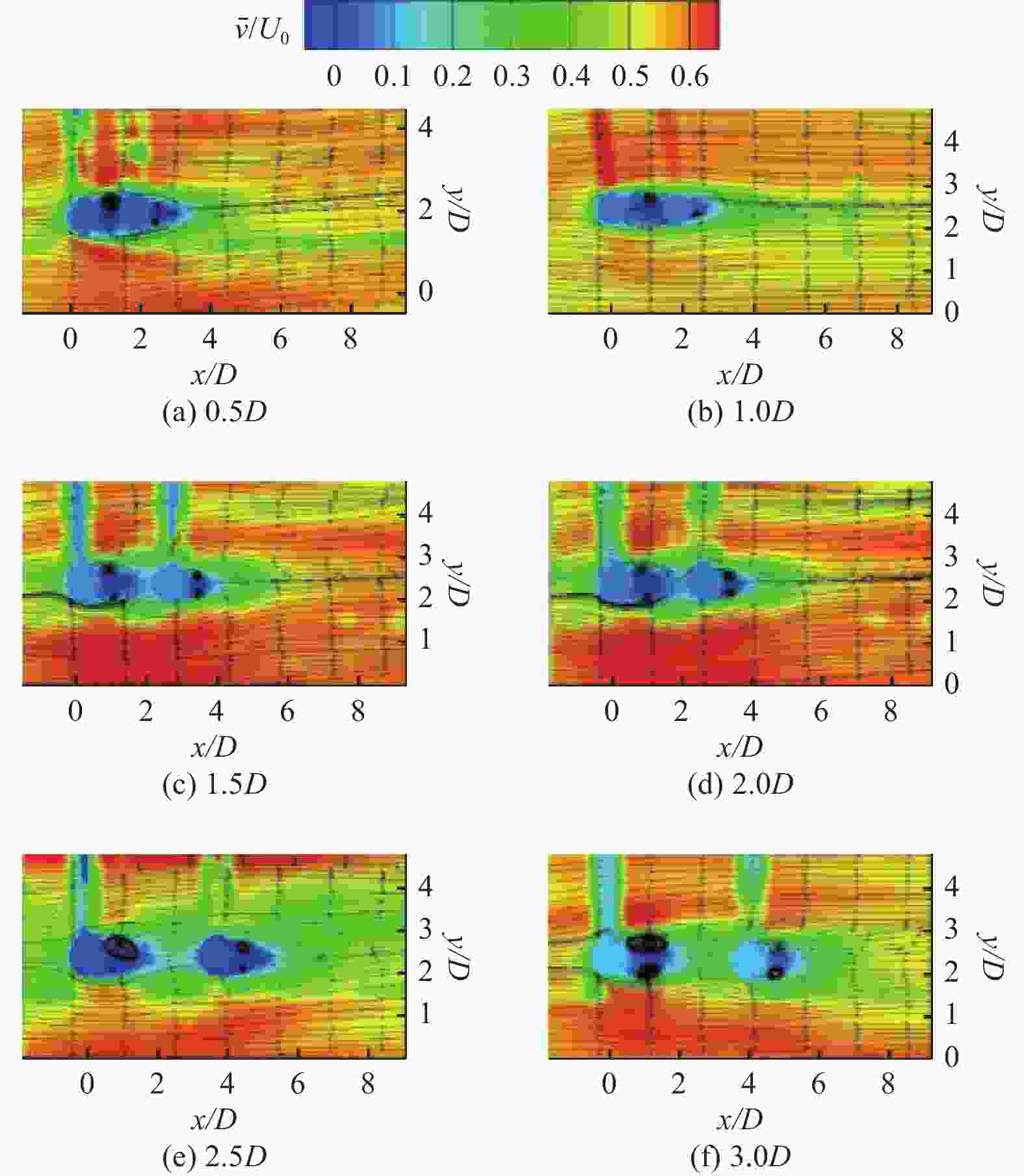
摘要: 为掌握边界层粒子周围的流动结构，利用粒子图层测速(PIV)技术在雷诺数为500 ~ 2000范围内，对3种不同直径、6种不同间距下的粒子周围的流场特性进行了测量. 对流场特性分析的结果表明，随着流体速度和粒子直径的增加，粒子后端的漩涡区域逐渐被增强，会形成单个漩涡、镜像对称漩涡、一大一小旋向相反漩涡3种模式. 在观测的试验粒子中，10 mm粒子后端的漩涡区域最为显著；当粒子间距增大到一定阈值后，粒子后端的漩涡区域便不再随着间距的增大而被增强. 研究结果为进一步揭开边界层粒子周围的流动结构提供了试验依据.Abstract: To comprehend the flow structures surrounding particles within the boundary layer, particle image velocimetry (PIV) technique was employed to measure the flow field characteristics around particles of three distinct diameters and six different spacings within the Reynolds number range of 500 to 2000. The analysis results of the flow field characteristics reveal that with escalating fluid velocity and particle diameter, the vortex region behind the particles progressively intensified, exhibiting three distinctive modes: a singular vortex, mirror-symmetric vortices, and large-small oppositely rotating vortices. Among the observed experimental particles, the vortex region behind 10 mm particles displayed the most pronounced characteristics. However, upon reaching a certain threshold of particle spacing, the enhancement of the vortex region behind the particles ceased with further increases in spacing. These research findings serve as experimental evidence toward further elucidating the flow structures around particles within the boundary layer.
-
Key words:
- boundary layer /
- particle image velocimetry (PIV) /
- flow characteristics /
- vortex /
- particles
-
边界层的流动在自然界中十分常见，而含有固体颗粒的流动也常出现在各种领域，如管道内和槽内的流动、各种气−固两相流、液−固两相流以及钝体绕流等. 已有相关研究表明[1-2]，物质的动量和流体运输会受到由固体颗粒和壁面而产生的边界层的显著影响. 各领域对边界层以及伴随边界层产生的流动现象也进行了研究. 在边界层这一复杂的流场中开展详细的可视化、阐明构造的基础研究，同样也对改善环境和工业问题有积极作用.
唐扬杨等[1]通过模拟在方柱中心开孔通入旋流气体，探究钝体绕流漩涡脱落规律，结果发现漩涡脱落的主导原因为中心通孔引起的旋流涡，且脱落涡的尺度变大. 于定勇等[2]利用Fluent软件模拟正方形排列四圆柱在Re = 3900条件下，间距比与升、阻力系数以及斯特劳哈尔数之间的关系. Wang 等[3]在Re = 8000时，对不同间距比和来流角度进行四圆柱绕流物理模型试验，详细研究间距比和角度对升、阻力系数以及漩涡脱落形态的影响. 陆雨洲等[4]通过粒子图层测速（Particle Image Velocimetry，PIV）技术对直径与厚度比为5的圆盘近尾迹流场结构的研究. 发现在Re = 22400时，回流区具有较好的对称性，且通过本征正交分解 ( Proper Orthogonal Decomposition，POD )重构后的数据发现流向雷诺正应力和切应力峰值出现在回流区两侧剪切层，横向雷诺正应力峰值出现在回流区驻点附近. 杨纪伟等[5]归纳总结了流场中放置双圆柱、三圆柱、四圆柱和、一主一副或一主两副圆柱时，流场结构随圆柱相对位置的变化规律. 许相辉等[6]利用层析PIV技术，观测直径为12 mm的圆柱三维尾流场，成功获得圆柱体后方典型的三维卡门涡流场. 王勇等[7]利用PIV技术测量Re = 27400下直径为20 mm的圆柱后方绕流尾迹，得到圆柱后方存在低速回流区，绕流尾迹中漩涡脱落频率对应的斯特劳哈尔数在0.2左右. 王轩等[8]利用高时间分辨率PIV技术对凹壁面上下游湍流边界层进行研究，对湍流边界层内的相干结构进行了阐释.孙姣等[9]利用PIV技术在平板湍流边界层内对颗粒的运动行为进行研究，发现大颗粒在湍流度、雷诺应力、脉动速度、喷射数目以及动量交换等方面都强于小颗粒. Ramezani等[10]利用PIV技术对5个球形颗粒在方形管道内，Re = 100时的流动进行试验测量，并与直接数值模拟(PR-DNS)的结果进行详细比较. 同时对I/Dp (为相邻颗粒之间的中心距与粒子直径的比值)为1.38和2.19的两种不同颗粒分离距离的结果比较，用PIV试验数据验证了PR-DNS数值计算结果，两者结果吻合良好. Piotr [11]在恒定的管径下，对5种不同直径的球和9种不同间距的球周围的流动进行研究，得到带有球镶件扰流的圆管内流动的计算机模拟结果. 分析球直径和它们的纵向距离对湍流压降的影响结果表明，对于整个测试范围的球直径和它们的纵向排列，存在解析依赖性. Nino等[12]对明槽水流近壁区颗粒与湍流的相互作用的研究发现，颗粒在流体夹带作用下流向速度分量小于当地流体速度流向分量，法向速度分量则大于当地流体法向速度. Muammer [13]通过PIV技术研究单球布置和等边三角形三球布置的流动结构，得到在两个下游球体上的平均流型大多数情况下几乎是对称的，但剪切现象和脱落涡的相互作用依旧可导致整个流场的高波动率.
由上述研究可知，国内外对于边界层流动中引起的扰动研究对象前期多选取圆柱体，后面开始转向球形颗粒，而对球形颗粒在边界层的流动特性研究还处于探索阶段，关于固定圆形颗粒在流场中的作用还需做大量研究，以将其流动特性的优点发挥到更多领域. 本研究将球形粒子设置在一个固定尺寸的平板上，通过改变来流速度和在平板上平行移动粒子来改变粒子之间的间距作为本研究的自变量，并利用PIV技术对含有固体粒子的复杂边界层中的流动进行可视化分析，得到实际的流场数据，进而比较相同直径不同粒子间隔下的情况，再比较不同直径和流体速度的情况，考察流体流经球形颗粒后流动行为的不同，以阐明流动结构的变化.
1. 试验设置与参数
1.1 试验模型
本试验在回流水槽内进行，如图1所示. 水槽工作段宽400 mm，高200 mm，长1000 mm，在摄影区域内设置尺寸分别为4、7和10 mm，材质为钢材的球形模型以及长为750 mm、宽为400 mm的平板，如图2所示. 第一个球形模型设置在距离平板前端100 mm的中心位置，此处受水槽内外侧壁面影响较小. 水槽内水流速度的改变通过控制水泵叶轮转速来实现.
在回流水槽内放入水作为工作流体，并混入示踪粒子. 试验中来流速度为0.16和0.21 m/s，环境温度为20 ℃，选用三菱化学 Sepabeads SP20SS示踪粒子，粒子直径15%为 63 μm以下，55%为63 ~ 75 μm，30%为75 μm以上. PIV分析软件采用IDT ProVision分析工具，激光发生器为二极管泵浦固体激光器(Diode Pumped Solid State Laser，DPSSL)，高速摄像机型号为Photoron FASTCAM SA3，设置快门速度为1/500 s，帧率为500 帧/s，采集样本数为6000张. 在对象模型及平板上照射激光薄片光，用高速摄像机拍摄通过照射表面的示踪粒子，试验示意图和试验场景如图3、图4所示. 在试验中，进行(x,z)截面和(x,y)截面2个截面的可视化试验. 激光薄片的光照射(x,z)截面和(x,y)截面并都穿过模型中心.
设置多个模型进行拍摄时，将粒子间隔设定为I，如图5所示.
图中：D为球形粒子直径；I为球形粒子模型间隔，I = xD (x = 0.5 ~ 3.0).
1.2 PIV解析条件
PIV分析条件见表1. 根据1.1节设置试验高速摄像机，拍摄条件见表2. 不同转速下工作流体流经不同直径粒子模型时的雷诺数见表3.
表 1 PIV分析条件Table 1. Analysis condition of PIV分析条件 方向 (x,y)截面 (x,z)截面 图片分析数量 1000 1000 网格节点数 110 × 50 110 × 50 表 2 拍摄条件Table 2. Filming conditions相机设置 方向 (x,y)截面 (x,z)截面 帧率/(帧·s-1) 500 500 快门速度/s 1/500 1/500 图像大小 1024 × 416 1024 × 416 平均流速/(m·s-1) 0.16 , 0.21 0.16 , 0.21 图片数量 3000 3000 表 3 雷诺数Table 3. Reynolds number模型尺寸/mm 转速/(r·min−1) 2000 2500 4 562 737 7 983 1291 10 1405 1844 为方便后续对PIV 试验结果进行分析，对PIV计算得到的测量值进行无量纲化. U0为主速度，x方向上的平均速度无量纲化的结果为
$ \bar{u} / U_0 $ ，y方向上的平均速度无量纲化的结果为$\bar{v} / U_0$ .2. 试验结果与分析
2.1 低流速(x,z)截面平均流速及流线分析
图6为观测区域内4 mm颗粒在不同粒子间距，流体速度为0.16 m/s时(x,z)截面的瞬时平均流速及流线分布图. 由图可知，4 mm两粒子的后端在I/D = 0.5 ~ 3.0均发生明显的剥离现象，且在同一间距下，前后两粒子剥离形成的伴流区域较相似. 剥离现象产生原因是由于物体黏性的影响，流体不能沿着物体表面流动而从物体上剥离. 随着两粒子之间的间距逐渐增大，粒子后端剥离形成的伴流区域也逐渐变长. 同时部分粒子后端会形成漩涡. 两粒子之间所形成漩涡最显著，漩涡中心位于x/D=2.0处（图6(d)）. 图中还可以看出粒子对来流产生阻力，形成显著的减速区域，且减速区域多分布于z/D=2.0之下；2.5D粒子间距时减速区域最宽泛，减速区域分布在z/D=4.0之下.
图 6 4 mm粒子平均流体速度和(x,z)平面流线分布图（0.16 m/s）Figure 6. Mean fluid velocity and streamlines in (x,z)-plane (0.16 m/s) of 4 mm particle图7为观测区域内7 mm颗粒在不同粒子间距，流体速度为0.16 m/s时，(x,z)截面的瞬时平均流速及流线分布图. 对比图6和图7可知：粒子直径为7 mm时，两粒子后端剥离形成的伴流区域变得更长，且在I/D≤2.0的条件下，两粒子之间形成明显的漩涡区域，I/D=1.5时最为显著，漩涡中心大致位于x/D=1.8处. I/D=0.5和I/D=1.0时，减速区域分布于z/D=3.0之下；I/D=1.5 ~ 3.0时，几乎分布于z/D=2.0以下.
图 7 7 mm粒子平均流体速度和(x,z)平面流线分布(0.16 m/s)Figure 7. Mean fluid velocity and streamlines in (x,z)-plane (0.16 m/s) of 7 mm particle图8为观测区域内10 mm颗粒在不同粒子间距，流体速度为0.16 m/s时(x,z)截面的瞬时平均流速及流线分布图. 由图可见，当粒子直径变为10 mm时，与4 mm 和7 mm的粒子相比，两粒子之间形成更加明显的漩涡区域，在I/D=0.5 ~ 3.0时均有出现. I/D=0.5 ~ 1.5时两粒子间均有较明显漩涡区域，I/D=2.0 ~ 3.0时两粒子间有形成交错涡的趋势. 10 mm粒子所造成的减速区域均分布于z/D=1.0以下.
图 8 10 mm粒子平均流体速度和(x,z)平面流线分布(0.16 m/s)Figure 8. Mean fluid velocity and streamlines in (x,z)-plane (0.16 m/s) of 10 mm particle粒子之间形成漩涡的原因是流体接触粒子受阻后动能和压能相互转换，且压强沿粒子周向及边界层的厚度方向发生变化. 同时在边界层外部流体以及后面粒子前端的较大压强作用下，迫使两粒子之间边界层内部压强较小的质点向相反方向流动，从而使边界层增厚，形成漩涡. 而当混合流体流经此区域时将会达到更好的掺混效果.
2.2 高流速(x,z)截面平均流速及流线分析
图9为观测区域内4 mm颗粒在不同粒子间距，流体速度为0.21 m/s时(x,z)截面的瞬时平均流速及流线分布图. 由图可知，当流体速度由0.16 m/s变为0.21 m/s，对于4 mm粒子剥离形成的伴流区域影响效果不显著，整体变化趋势几乎相同，依旧是I/D=1.5时，两粒子间的漩涡区域最显著，漩涡中心大致位于x/D=1.7处. 但I/D=1.0 ~ 2.0 时，两粒子之间的伴流区域开始转变为漩涡区域. 减速区域在I/D=0.5和I/D=1.0时，分布于z/D=3.0以下，相较于低流速的情况，减速区域反而变得宽泛. 在I/D=1.5 ~ 3.0时，减速区域分布在z/D=2.0以下.
图 9 4 mm粒子平均流体速度和(x,z)平面流线分布(0.21 m/s)Figure 9. Mean fluid velocity and streamlines in (x,z)-plane (0.21 m/s) of 4 mm particle图10为观测区域内7 mm颗粒在不同粒子间距，流体速度为0.21 m/s时(x,z)截面的瞬时平均流速及流线分布图. 由图可知，对于7 mm粒子I/D≤2.0的情况来说，两粒子之间的漩涡区域变得更加明显，特别是I/D=1.0时，漩涡区域明显增强. 同时，在I/D=2.5 和I/D=3.0粒子间距时，首次分别在第1个粒子后端和第2个粒子后端出现漩涡区域，漩涡中心分别位于x/D=1.0和x/D=5.2处. 流速变为0.21 m/s后，7 mm粒子所造成的减速区域基本分布在z/D=1.0以下.
图 10 7 mm粒子平均流体速度和(x,z)平面流线分布(0.21 m/s)Figure 10. Mean fluid velocity and streamlines in (x,z)-plane (0.21 m/s) of 7 mm particle图11为不同粒子间距，流体速度为0.21 m/s时(x,z)截面的瞬时平均流速及流线分布图. 由图可知，对于10 mm粒子来说，两粒子之间的漩涡区域变得更加显著，伴流区域并无明显变化，减速区域依旧分布在z/D=1之下. 综合图9 ~ 图11可知，增加流体流速至0.21 m/s，对于粒子后端的伴流区域无显著影响，对于两粒子之间边界层形成的漩涡区域有一定的增强作用，对减速区域在(x,z)截面起到削弱作用.
图 11 10 mm粒子平均流体速度和(x,z)平面流线分布(0.21 m/s)Figure 11. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 10 mm particle根据(x,z)截面的平均流速分布情况可以得出，当粒子直径逐渐增大时，在(x,z)截面中所造成的流速减小的区域变得越来越小.
2.3 低流速(x,y)截面平均流速及流线分析
图12为观测区域内4 mm颗粒在不同粒子间距，流体速度为0.16 m/s时(x,y)截面的瞬时平均流速及流线分布图. 由图可知，(x,y)截面整体流向与(x,z)截面一致，均为从左至右. 与图6对比，(x,y)截面在第1个粒子后端出现漩涡区域，第2个粒子后端大多数为伴流，个别出现未完全形成的漩涡区域. I/D≥1.5 时出现旋向相反的对称漩涡，在I/D=2.5 时，漩涡区域最为显著，漩涡中心位于x/D=0.8处. 且发现随着粒子的间距增大，低速区域范围呈现一种先增大后减小的趋势.
图 12 4 mm粒子平均流体速度和(x,y)平面流线分布(0.16 m/s)Figure 12. Mean fluid velocity and streamlines in (x,y)-plane (0.16 m/s) of 4 mm particle图13为观测区域内7 mm颗粒在不同粒子间距，流体速度为0.16 m/s时(x,y)截面的瞬时平均流速及流线分布图. 由图可知，7 mm粒子在I/D≥1.0时，在第1个粒子后端出现漩涡区域（I/D≥1.5时，漩涡区域旋向相反），I/D=3.0时最为显著，漩涡中心位于x/D=1.0处. 除I/D=1.0之外，第2个粒子后端均出现漩涡区域. I/D=2.5时，漩涡区域的旋向相反并呈现错位对称的现象. I/D=3.0时，漩涡区域出现类似卡门涡街，此时漩涡区域最为显著，漩涡中心位于x/D=5.0处. 该条件下低速区域较图12显著减少，且主要集中在粒子周围.
图 13 7 mm粒子平均流体速度和(x,y)平面流线分布(0.16 m/s)Figure 13. Mean fluid velocity and streamlines in (x,y)-plane (0.16 m/s) of 7 mm particle图14为观测区域内10 mm颗粒在不同粒子间距，流体速度为0.16 m/s时(x,y)截面的瞬时平均流速及流线分布图. 由图可知，10 mm两个粒子的后端均出现漩涡区域. 当 I/D =1.0和 I/D =2.5时，第1个粒子后端出现一大一小旋向相反的漩涡区域，原因是大漩涡侧湍流边界层流速差较大，导致更大的压强差，从而形成较大的漩涡区域；第2个粒子后端出现镜像对称的漩涡区域. 当I/D=2.5时，第1个粒子后端的漩涡区域最为显著，漩涡中心位于x/D=1.0处；当I/D=3.0时，第2个粒子后端的漩涡区域最为显著，漩涡中心位于x/D=4.8处. 同时，低速区域进一步减少，表明粒子直径对流场流速的影响是较为显著的，小粒子直径反而能造成更大范围的减速.
图 14 10 mm粒子平均流体速度和(x,y)平面流线分布(0.16 m/s)Figure 14. Mean fluid velocity and streamlines in (x,y)-plane (0.16 m/s) of 10 mm particle2.4 高流速(x,y)截面平均流速及流线分析
图15为观测区域内4 mm颗粒在不同粒子间距，流体速度为0.21 m/s时(x,y)截面的瞬时平均流速及流线分布图. 由图可知，4 mm粒子在第1个粒子后端，除当I/D=1.5之外，均出现漩涡区域，I/D=3.0时，漩涡区域最为显著，漩涡中心位于x/D=0.8处. 在第2粒子后端，当I/D=0.5、2.5和3.0时，出现漩涡区域，I/D=2.5时，漩涡区域最为显著，漩涡中心位于x/D=4.3处.
图 15 4 mm粒子平均流体速度和(x,y)平面流线分布(0.21 m/s)Figure 15. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 4 mm particle图16为观测区域内7 mm颗粒在不同粒子间距，流体速度为0.21 m/s时(x,y)截面的瞬时平均流速及流线分布图. 由图可知，对于7 mm粒子，当I/D=0.5和I/D=1.0时，两粒子后端的漩涡区域变得更加显著，同时两粒子后端所形成的大多数为一大一小的漩涡区域. 当I/D=2.5时，第1个粒子后端的漩涡区域最为显著，漩涡中心位于x/D=0.8处；当I/D=3.0时，第2个粒子后端的漩涡区域最为显著，漩涡中心位于x/D=4.0处.
图 16 7 mm粒子平均流体速度和(x,y)平面流线分布(0.21 m/s)Figure 16. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 7 mm particle图17为观测区域内10 mm颗粒在不同粒子间距，流体速度为0.21 m/s时(x,y)截面的瞬时平均流速及流线分布图. 由图可知，对于10 mm粒子，观测区域整体变化不大. 但当I/D=3.0时，整个观测流场的低速区域明显减少. 同时，两个粒子后端漩涡区域都最为显著，漩涡中心分别位于x/D=1.2、x/D=4.8处.
图 17 10 mm粒子平均流体速度和(x,y)平面流线分布(0.21 m/s)Figure 17. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 10 mm particle2.5 结果讨论
通过上述的结果分析，对于串列放置的双球颗粒在不同间距比的条件下对边界层流场结构所造成的影响，与Summer等[14]所描述的在0°攻角条件下，双圆柱绕流流态较为相似. 本研究中提出在间距比I/D<1.0时，前端粒子所形成的剥离区域会包裹在后端粒子周围；I/D=1.0 ~ 1.5时，后端粒子形成的剥离区域会脱落；I/D≥2.0时，前端粒子周围形成的剥离区域会脱落，而后随机从一端附着于后端粒子，后端粒子的剥离区域会完全脱落. 该结论与本试验结果也较为吻合.
3. 结 论
对4 mm、7 mm、10 mm粒子在I/D=0.5 ~ 3.0，两种不同流速0.16 m/s及0.21 m/s条件下，(x,z)截面和(x,y)截面的平均流速
$\bar{u} / U_0 $ 、$\bar{v} / U_0 $ 及流线分布情况分析得出以下结论.1) 当边界层中放置球形粒子后，对边界层结构产生明显影响，在两个粒子模型后方都会产生剥离区域(伴流和漩涡区域)，随着粒子模型之间的间隔增大，剥离区域在外观上是独立的.
2) 随着粒子直径的增大，无论是在(x,z)界面还是(x,y)截面，粒子造成的减速区域会变得越来越小. 同时，在(x,y)截面随着粒子直径的增大，流场的对称性也变得愈加明显.
3) 随着流体速度和粒子直径的增加，粒子后端的漩涡区域逐渐被增强，但不是线性变化的趋势.
颗粒对流场结构的扰动可以用于提高燃烧室燃料的掺混和燃烧的稳定性，同时进一步降低燃烧室污染气体的排放.
-
图 6 4 mm粒子平均流体速度和(x,z)平面流线分布图（0.16 m/s）
Figure 6. Mean fluid velocity and streamlines in (x,z)-plane (0.16 m/s) of 4 mm particle
图 7 7 mm粒子平均流体速度和(x,z)平面流线分布(0.16 m/s)
Figure 7. Mean fluid velocity and streamlines in (x,z)-plane (0.16 m/s) of 7 mm particle
图 8 10 mm粒子平均流体速度和(x,z)平面流线分布(0.16 m/s)
Figure 8. Mean fluid velocity and streamlines in (x,z)-plane (0.16 m/s) of 10 mm particle
图 9 4 mm粒子平均流体速度和(x,z)平面流线分布(0.21 m/s)
Figure 9. Mean fluid velocity and streamlines in (x,z)-plane (0.21 m/s) of 4 mm particle
图 10 7 mm粒子平均流体速度和(x,z)平面流线分布(0.21 m/s)
Figure 10. Mean fluid velocity and streamlines in (x,z)-plane (0.21 m/s) of 7 mm particle
图 11 10 mm粒子平均流体速度和(x,z)平面流线分布(0.21 m/s)
Figure 11. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 10 mm particle
图 12 4 mm粒子平均流体速度和(x,y)平面流线分布(0.16 m/s)
Figure 12. Mean fluid velocity and streamlines in (x,y)-plane (0.16 m/s) of 4 mm particle
图 13 7 mm粒子平均流体速度和(x,y)平面流线分布(0.16 m/s)
Figure 13. Mean fluid velocity and streamlines in (x,y)-plane (0.16 m/s) of 7 mm particle
图 14 10 mm粒子平均流体速度和(x,y)平面流线分布(0.16 m/s)
Figure 14. Mean fluid velocity and streamlines in (x,y)-plane (0.16 m/s) of 10 mm particle
图 15 4 mm粒子平均流体速度和(x,y)平面流线分布(0.21 m/s)
Figure 15. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 4 mm particle
图 16 7 mm粒子平均流体速度和(x,y)平面流线分布(0.21 m/s)
Figure 16. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 7 mm particle
图 17 10 mm粒子平均流体速度和(x,y)平面流线分布(0.21 m/s)
Figure 17. Mean fluid velocity and streamlines in (x,y)-plane (0.21 m/s) of 10 mm particle
表 1 PIV分析条件
Table 1. Analysis condition of PIV
分析条件 方向 (x,y)截面 (x,z)截面 图片分析数量 1000 1000 网格节点数 110 × 50 110 × 50 
下载: 导出CSV
表 2 拍摄条件
Table 2. Filming conditions
相机设置 方向 (x,y)截面 (x,z)截面 帧率/(帧·s-1) 500 500 快门速度/s 1/500 1/500 图像大小 1024 × 416 1024 × 416 平均流速/(m·s-1) 0.16 , 0.21 0.16 , 0.21 图片数量 3000 3000
下载: 导出CSV
-
[1] 唐杨杨, 李志强, 邸亚超, 等. 方柱-强旋组合旋涡脱落机制研究[J] . 推进技术,2014,35(8):1023 − 1029. [2] 于定勇, 张广成, 马朝晖. 湍流场多柱体绕流形态和水动力特性研究[J] . 中国海洋大学学报(自然科学版),2016,46(6):52 − 59. [3] WANG X K, GONG K. Flow around four cylinders arranged in a square configuration[J] . Journal of Fluids and Structures,2013,43:179 − 199. doi: 10.1016/j.jfluidstructs.2013.08.011 [4] 陆雨洲, 徐庶民, 钟伟, 等. 圆盘绕流近尾迹实验研究[J] . 实验流体力学,2013,27(6):19 − 25. [5] 杨纪伟, 滕丽娟, 胥战海. 多圆柱绕流旋涡脱落和流场形态概论[J] . 人民长江,2009,40(3):66 − 68, 86. doi: 10.3969/j.issn.1001-4179.2009.03.025 [6] 许相辉, 蒋甲利, 牛中国, 等. 圆柱尾流场的Tomo-PIV测量[J] . 实验流体力学,2015,29(5):60 − 64. [7] 王勇, 郝南松, 耿子海, 等. 基于时间解析PIV的圆柱绕流尾迹特性研究[J] . 实验流体力学,2018,32(1):64 − 70. [8] 王轩, 范子椰, 陈乐天, 等. 流向凹曲率壁面湍流边界层的TRPIV实验研究[J] . 实验流体力学,2022,36(6):1 − 9. [9] 孙姣, 轩瑞祥, 高天达, 等. 湍流边界层内不同粒径颗粒行为的PIV实验研究[J] . 化学工程,2018,46(12):59 − 63. [10] RAMEZANI M, SUNA B, SUBRAMANIAMA S, et al. Detailed experimental and numerical investigation of fluid-particle interactions of a fixed train of spherical particles inside a square duct[J] . International Journal of Multiphase Flow,2018,103:16 − 29. doi: 10.1016/j.ijmultiphaseflow.2018.01.013 [11] PIOTR B J. Numerical study of the thermo-hydraulic characteristics in a circular tube with ball turbulators. Part 1: PIV experiments and a pressure drop[J] . International Journal of Heat and Mass Transfer,2014,74:48 − 59. doi: 10.1016/j.ijheatmasstransfer.2014.02.074 [12] NINO Y, GARCIA M H. Experiments on particle-turbulence interactions in the near-wall region of an open channel flow: implications for sediment transport[J] . Journal of Fluid Mechanics,2006,326:285 − 319. [13] MUAMMER O, Flow structures around an equilateral triangle arrangement of three spheres[J]. International Journal of Multiphase Flow, 2013, 53: 54-64. [14] SUMMER D, PRICE S, PAÏDOUSSIS M P. Flow-pattern identification for two staggered circular cylinders in cross-flow[J] . Journal of Fluid Mechanics,2000,411:263 − 303. doi: 10.1017/S0022112099008137 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 282
- HTML全文浏览量: 130
- PDF下载量: 63
- 被引次数: 0
