基于视觉的坐便器清洁度检测方法应用研究

彭勇; 张华; 高延峰

doi:10.12299/jsues.23-0209

基于视觉的坐便器清洁度检测方法应用研究

doi: 10.12299/jsues.23-0209

上海工程技术大学机械与汽车工程学院, 上海 201620

基金项目: 国家自然科学基金资助（61763030）；国家重点研发计划“智能机器人”重点专项资助（2018YFB1305304）

详细信息

作者简介:
彭勇：彭　勇（1998−），男，硕士生，研究方向为计算机视觉。E-mail：1137873479@qq.com

通讯作者:
张　华（1964−），男，教授，博士，研究方向为移动机器人、焊接自动化。E-mail：hzhang@sues.edu.cn

中图分类号: TP391
计量
- 文章访问数: 10
- HTML全文浏览量: 6
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-25
- 网络出版日期: 2024-11-14
- 刊出日期: 2024-09-30

Application research of visual-based method for detecting toilet cleanliness

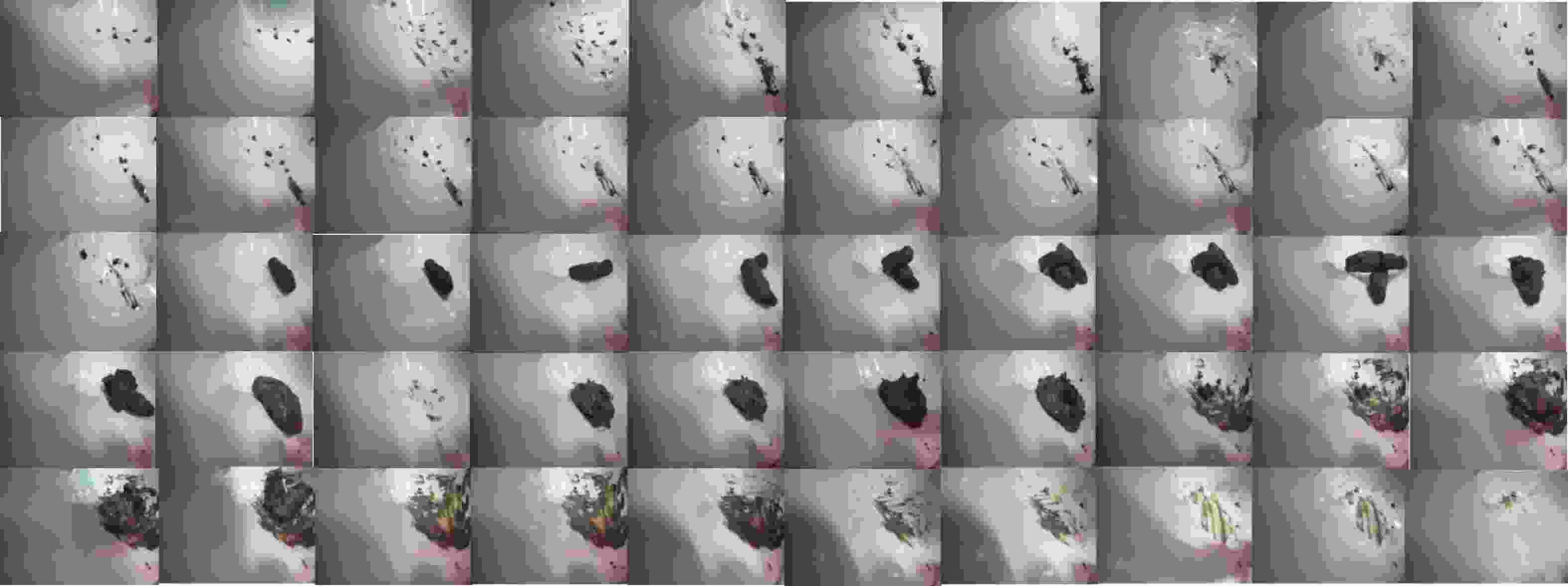
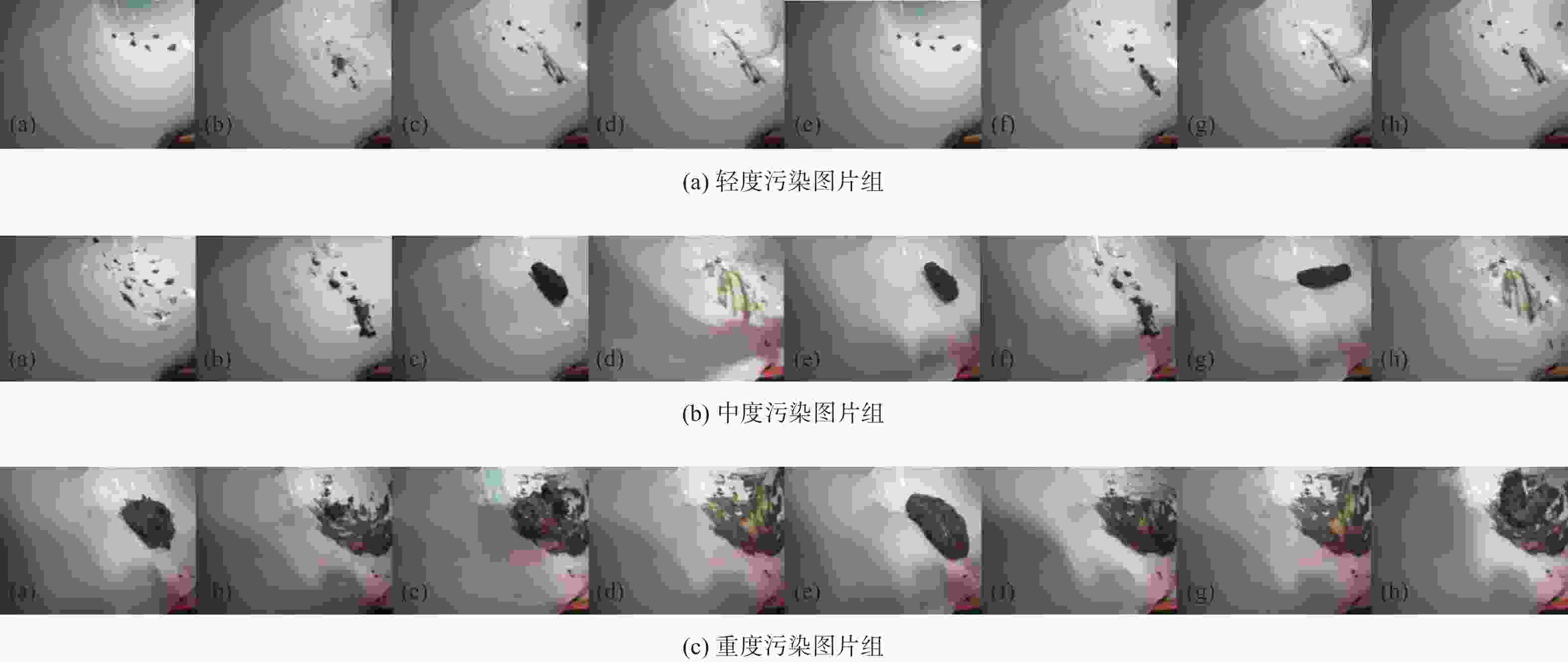
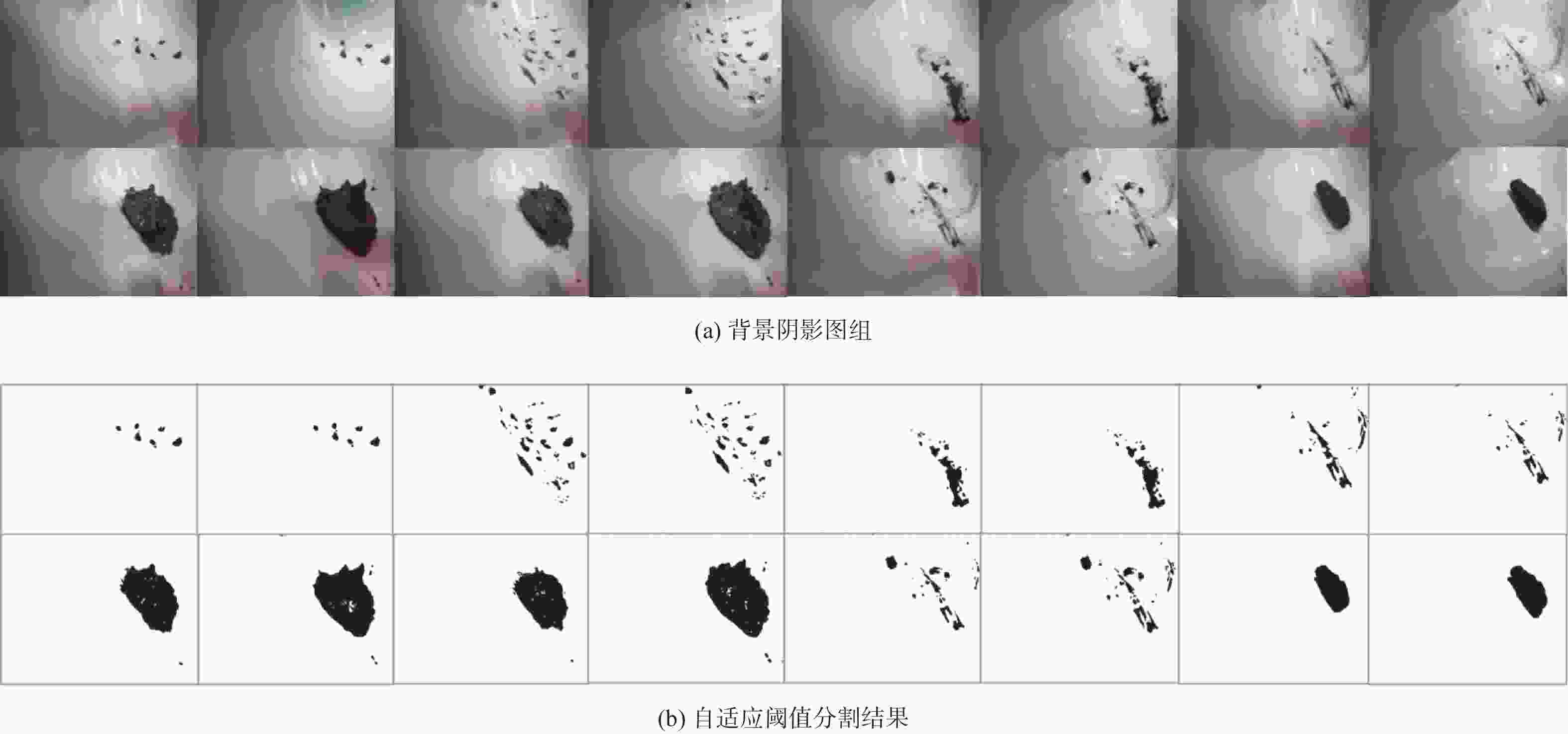
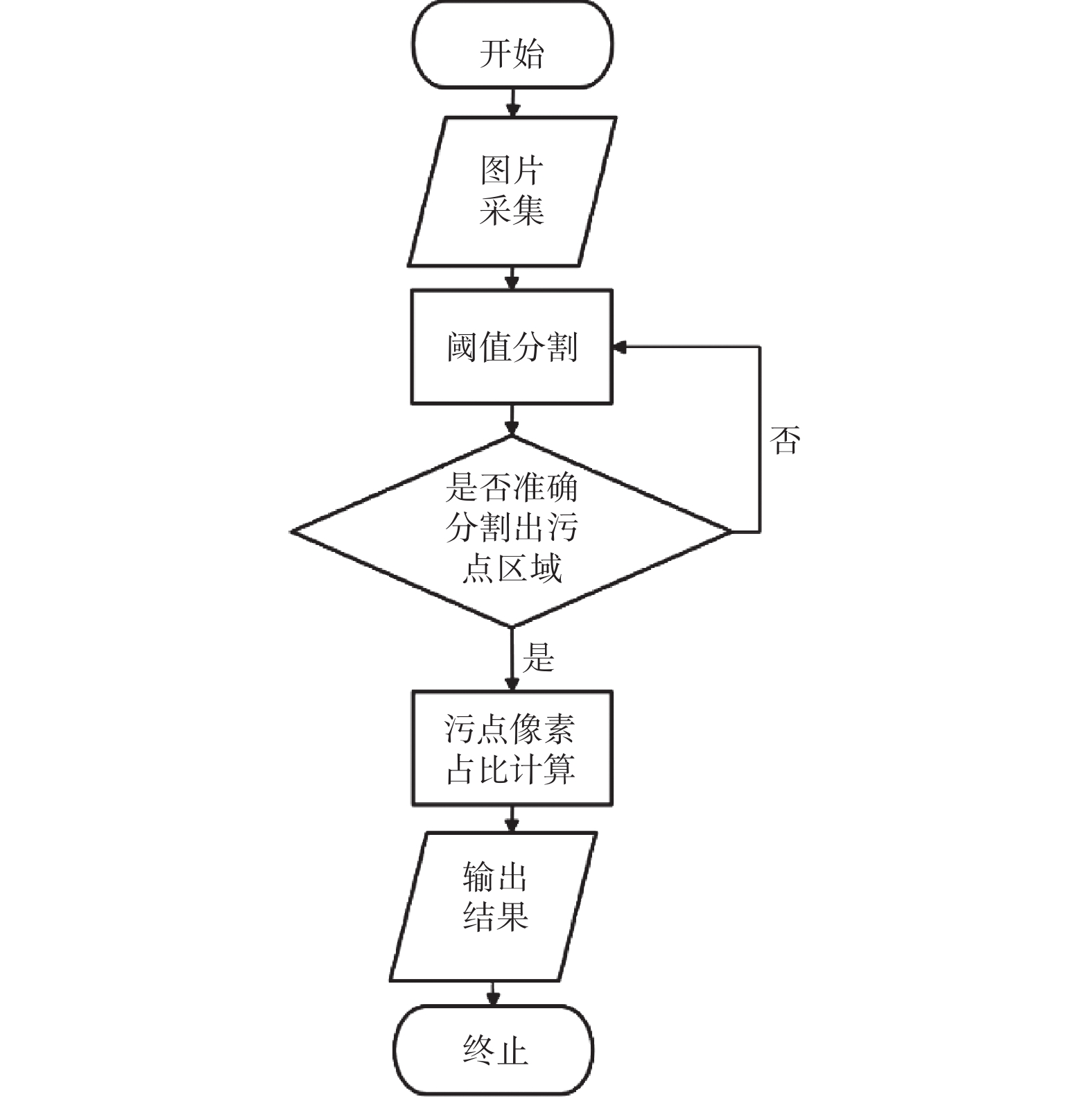
School of Mechanical and Automotive Engineering , Shanghai University of Engineering Science, Shanghai 201620, China

摘要

摘要: 目前二便智能护理机器人只在排便结束后对坐便器斗进行一次恒定大水量冲洗，没有相应清洁度检测环节，导致残存的粪便容易造成空气异味和细菌滋生，甚至疾病传染。针对于此，提出基于视觉的两种清洁度检测方法：一种是通过计算污点像素占比来进行坐便器清洁度的评估，另一种是采用图像模板匹配的方法来检测坐便器的清洁度。试验结果表明：采取自适应阈值分割来计算污点像素占比时能够很好地克服背景阴影的影响，且能够准确地区分出不同污染程度的照片组，达到便斗清洁度检测的目的。
- 清洁度 /
- 图像处理 /
- 图像相似度 /
- 自适应阈值分割
Abstract: At present, intelligent nursing robots for secondary defecation only rinse the bucket with a constant amount of water after defecation, without corresponding cleanliness testing. The remaining feces can easily cause air odor and bacterial growth, and even spread diseases. In response to this, two visual based cleanliness detection methods were proposed: one is to evaluate the cleanliness of the toilet by calculating the proportion of dirty pixels, and the other is to use image template matching method to detect the cleanliness of the toilet. Experimental results show that by using adaptive threshold segmentation to calculate the proportion of dirty pixels, it can effectively overcome the influence of background shadows and accurately distinguish photo groups with different levels of pollution, thus achieving the goal of detecting the cleanliness of the toilet.
- cleanliness /
- image processing /
- image similarity /
- adaptive threshold segmentation

HTML全文

图 1 像素占比算法流程图

Figure 1. Pixel proportion algorithm flowchart

下载: 全尺寸图片幻灯片

图 2 数字图像示意图

Figure 2. Digital image schematic

下载: 全尺寸图片幻灯片

图 3 自适应阈值选取示意图

Figure 3. Schematic diagram of adaptive threshold selection

下载: 全尺寸图片幻灯片

图 4 SSIM算法原理图

Figure 4. Schematic diagram of SSIM algorithm

下载: 全尺寸图片幻灯片

图 5 灰度直方图

Figure 5. Grayscale histogram

下载: 全尺寸图片幻灯片

图 6 试验数据图

Figure 6. Experimental data graph

下载: 全尺寸图片幻灯片

图 7 污染程度图片分组

Figure 7. Pictures grouping by pollution levels

下载: 全尺寸图片幻灯片

图 8 全局阈值分割

Figure 8. Global threshold segmentation

下载: 全尺寸图片幻灯片

图 9 自适应阈值分割及污点像素占比

Figure 9. Adaptive threshold segmentation

下载: 全尺寸图片幻灯片

图 10 背景阴影图组

Figure 10. Background shadow group

下载: 全尺寸图片幻灯片

图 11 模板图像

Figure 11. Template image

下载: 全尺寸图片幻灯片

表 1 3种相似度评估算法匹配得分

Table 1. Matching score results of three similarity evaluation algorithms

图像	SSIM			余弦距离			皮尔逊相关性
图像	组一	组二	组三	组一	组二	组三	组一	组二	组三
a	0.94	0.91	0.86	0.98	0.99	0.91	0.93	0.95	0.56
b	0.92	0.91	0.81	0.92	0.96	0.89	0.93	0.89	0.51
c	0.92	0.92	0.76	0.93	0.93	0.87	0.92	0.75	0.14
d	0.91	0.83	0.78	0.98	0.90	0.92	0.94	0.72	0.34
e	0.94	0.89	0.85	0.98	0.91	0.94	0.94	0.68	0.50
f	0.92	0.87	0.78	0.92	0.93	0.90	0.92	0.79	0.23
g	0.91	0.89	0.78	0.97	0.90	0.92	0.94	0.64	0.35
h	0.93	0.86	0.77	0.94	0.89	0.93	0.93	0.71	0.25

下载: 导出CSV

参考文献(15)

[1]	周祖茗. 智能护理机器人的设计与研究[D]. 南昌: 南昌大学, 2012.
[2]	郝如茜. 白带显微图像中霉菌自动识别及清洁度判定的研究[D]. 成都: 电子科技大学, 2017.
[3]	茅靳丰, 朱国栋, 张虎, 等. 风管清扫机器人智能清洁度评估系统的研究[J] . 建筑热能通风空调,34,1:37 − 41.
[4]	刘翠, 徐立军, 文建鹏, 等. 洗碗机清洁度自动评分[J] . 电子产品可靠性与环境试验,2022,40(1):51 − 54.
[5]	王朝卿, 沈小林, 李磊. 图像相似度计算算法分析[J] . 现代电子技术,2019,42(9):31 − 34.
[6]	徐如如. 基于视觉的街道清洁度智能评估算法研究与实现[D]. 上海: 上海市计算技术研究所, 2021.
[7]	ĆIRIĆ D G. , PERIĆ Z H. , VUČIĆ N J, et al. Analysis of industrial product sound by applying image similarity measures[J] . Mathematics,2023,11(3):498.
[8]	SPYRIDONOS P, GAITANIS G, BASSUKAS I, et al. Gray Hausdorff distance measure for medical image comparison in dermatology: Evaluation of treatment effectiveness by image similarity[J]. Skin Research and Technology, 2013, 19(1). DOI: 10.1111/srt.12001.
[9]	涂德浴, 刘坤, 朱庆, 等. 基于机器视觉的钢管壁厚在线检测方法研究[J] . 计算机工程与应用,2022,58(16):249 − 256. doi: 10.3778/j.issn.1002-8331.2101-0127
[10]	章毓晋. 图像处理和分析教程[M]. 2版. 北京: 人民邮电出版社, 2016: 13−14.
[11]	李世文. 局部自适应分割算法在PCB图像处理中的应用[J] . 顺德职业技术学院学报,2019,17(2):9 − 12. doi: 10.3969/j.issn.1672-6138.2019.02.003
[12]	林恒青, 戴立庆. 基于局部自适应阈值分割和Hough变换的答题卡识别算法[J] . 桂林航天工业学院学报,2021,26(3):280 − 286.
[13]	张富贵, 秦芝乾, 吴雪梅, 等. 基于结构相似度算法的烟叶光照强度研究[J] . 中国农机化学报,2020,41(3):128 − 133.
[14]	孙小琳. 基于余弦相似度的自然计算方法研究及应用[D]. 哈尔滨: 哈尔滨师范大学, 2022.
[15]	张宇, 刘雨东, 计钊. 向量相似度测度方法[J] . 声学技术,2009,28(4):532 − 536.