Improved dragonfly algorithm based on chaos mapping and differential evolution
-
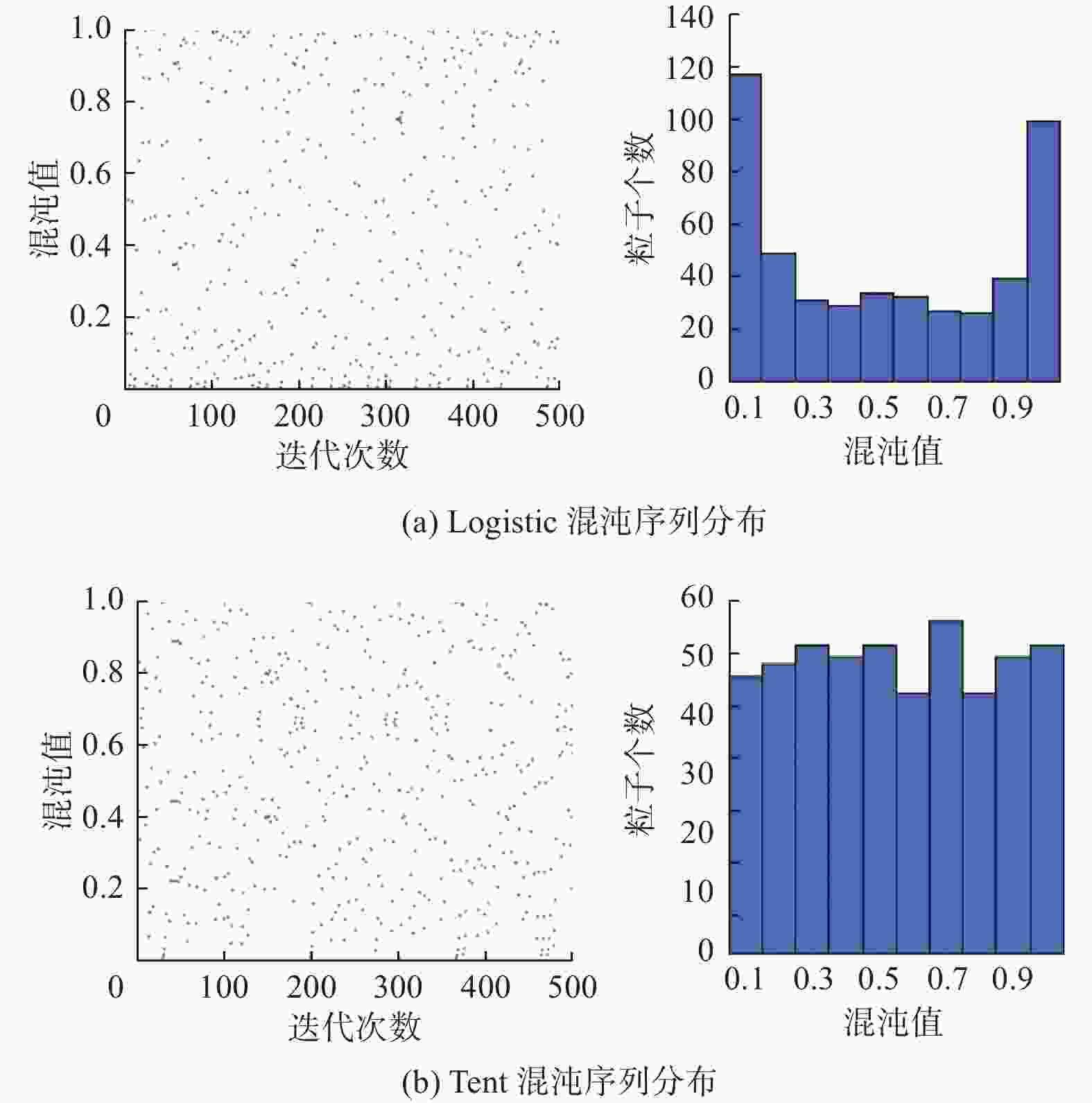
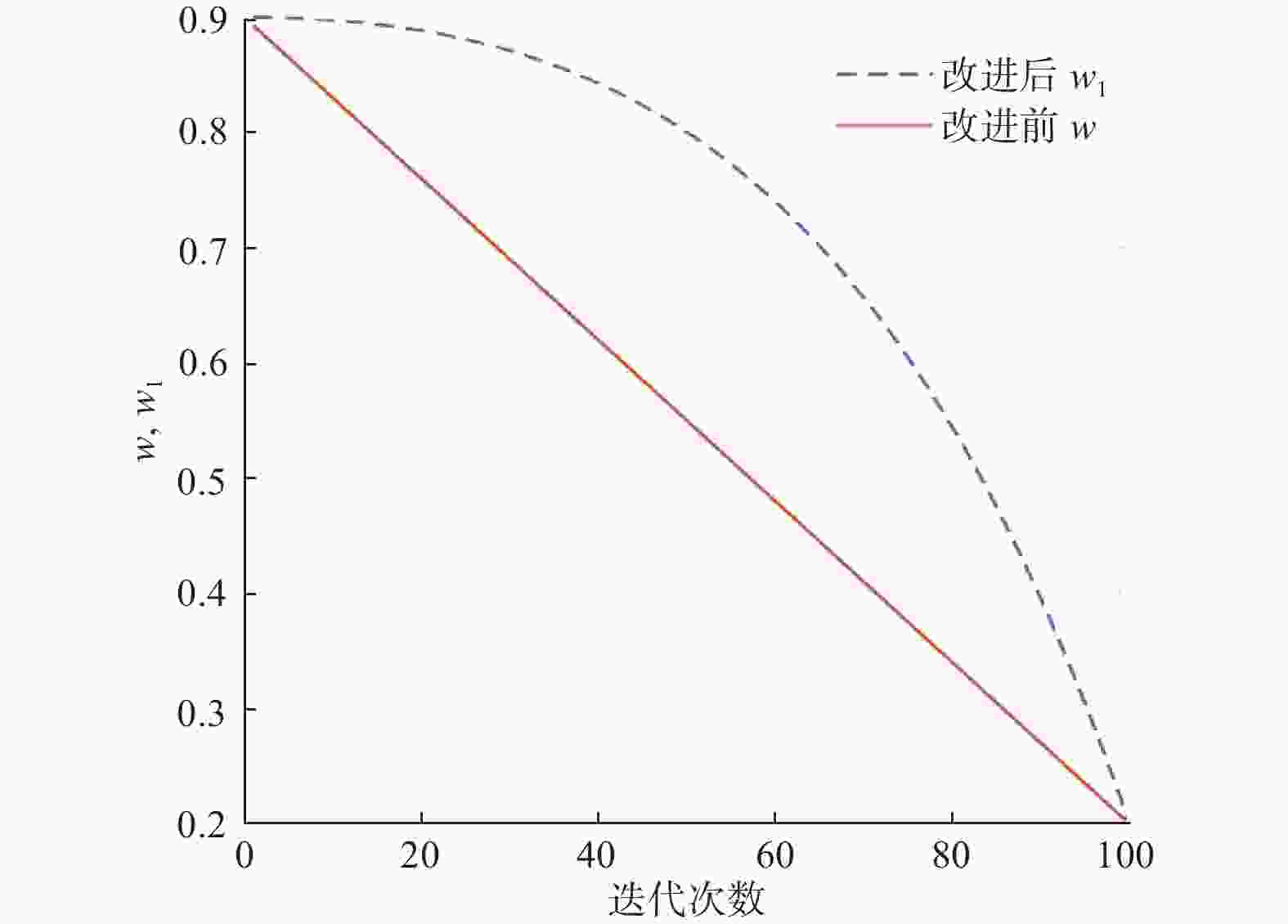
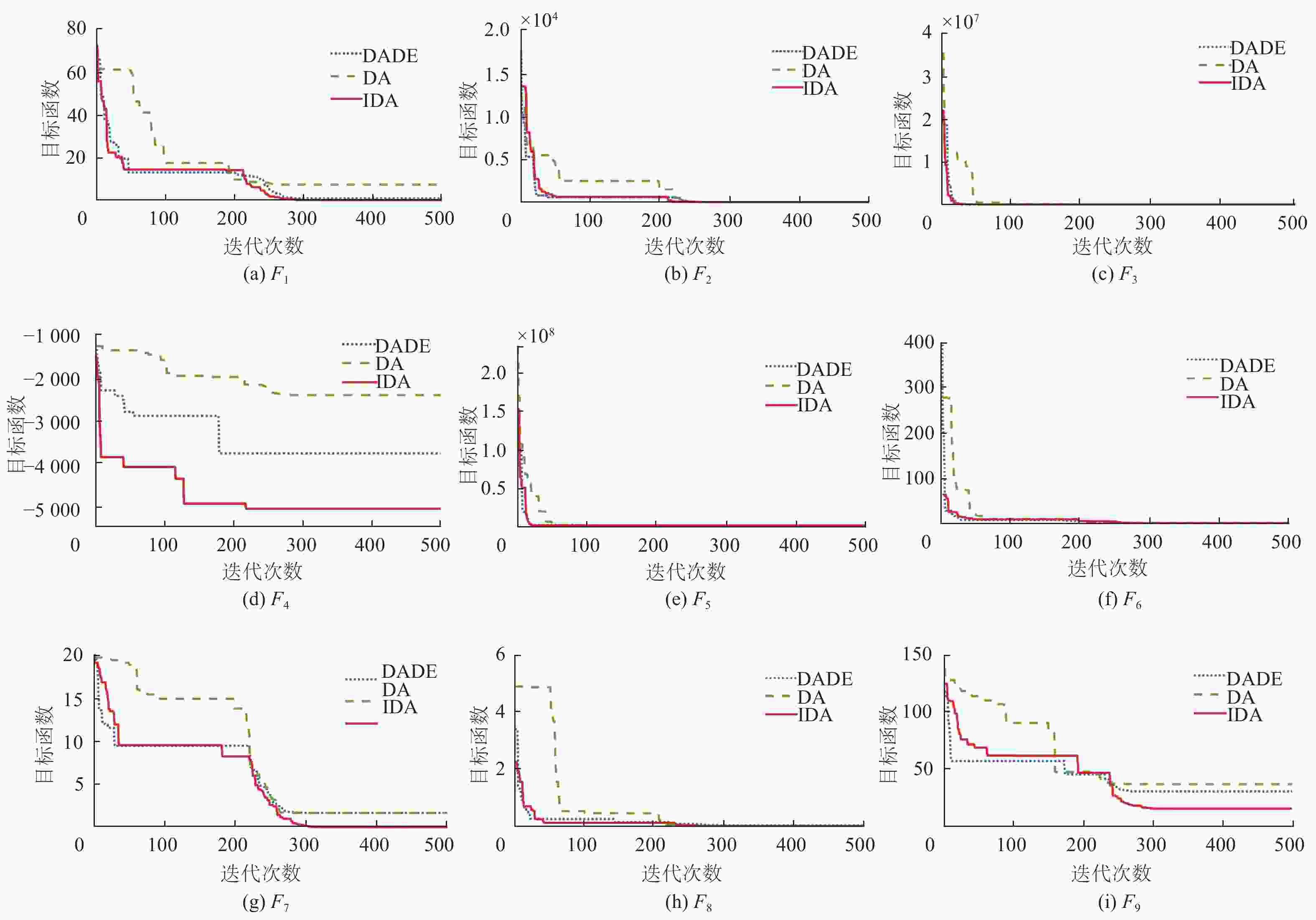
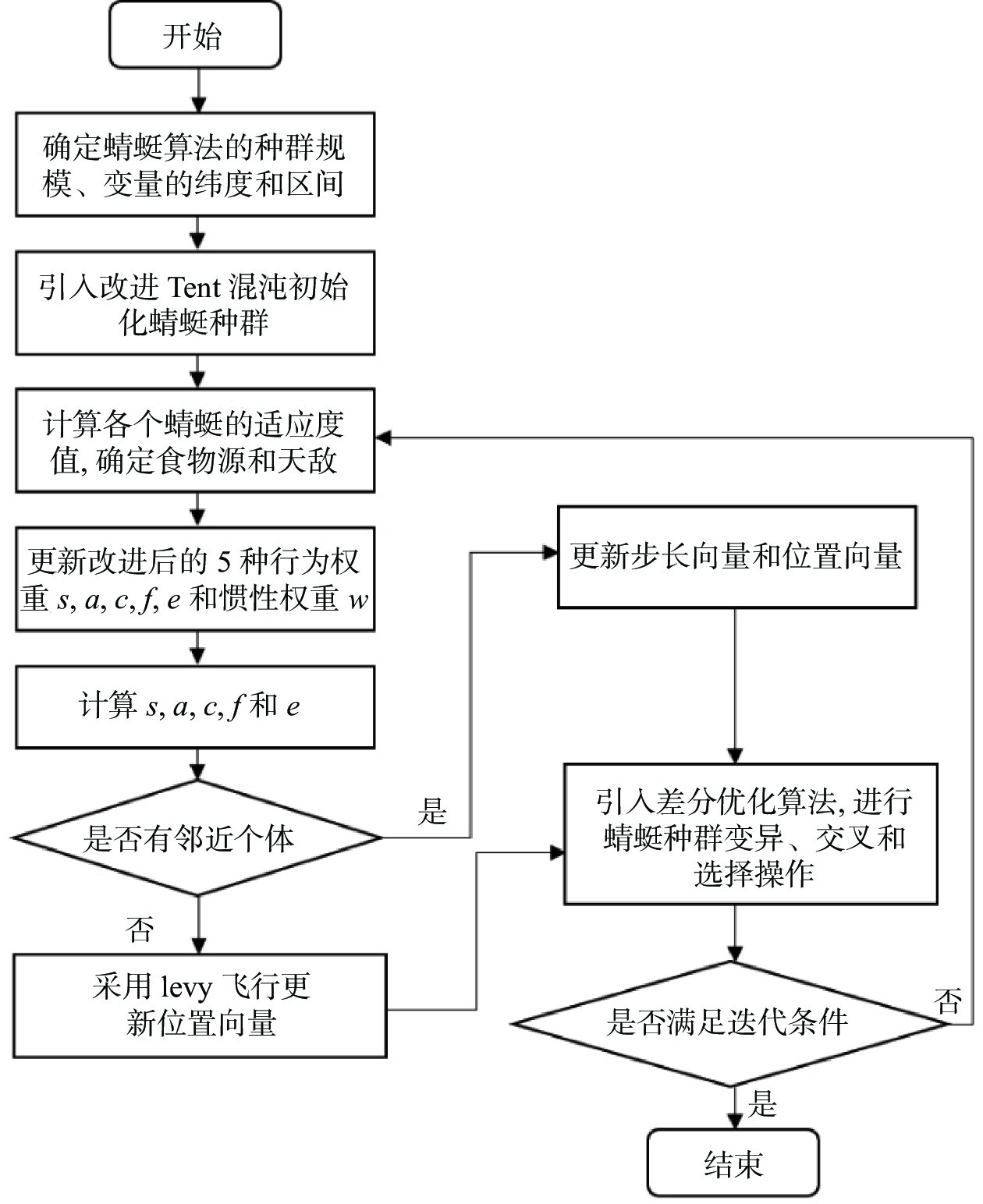
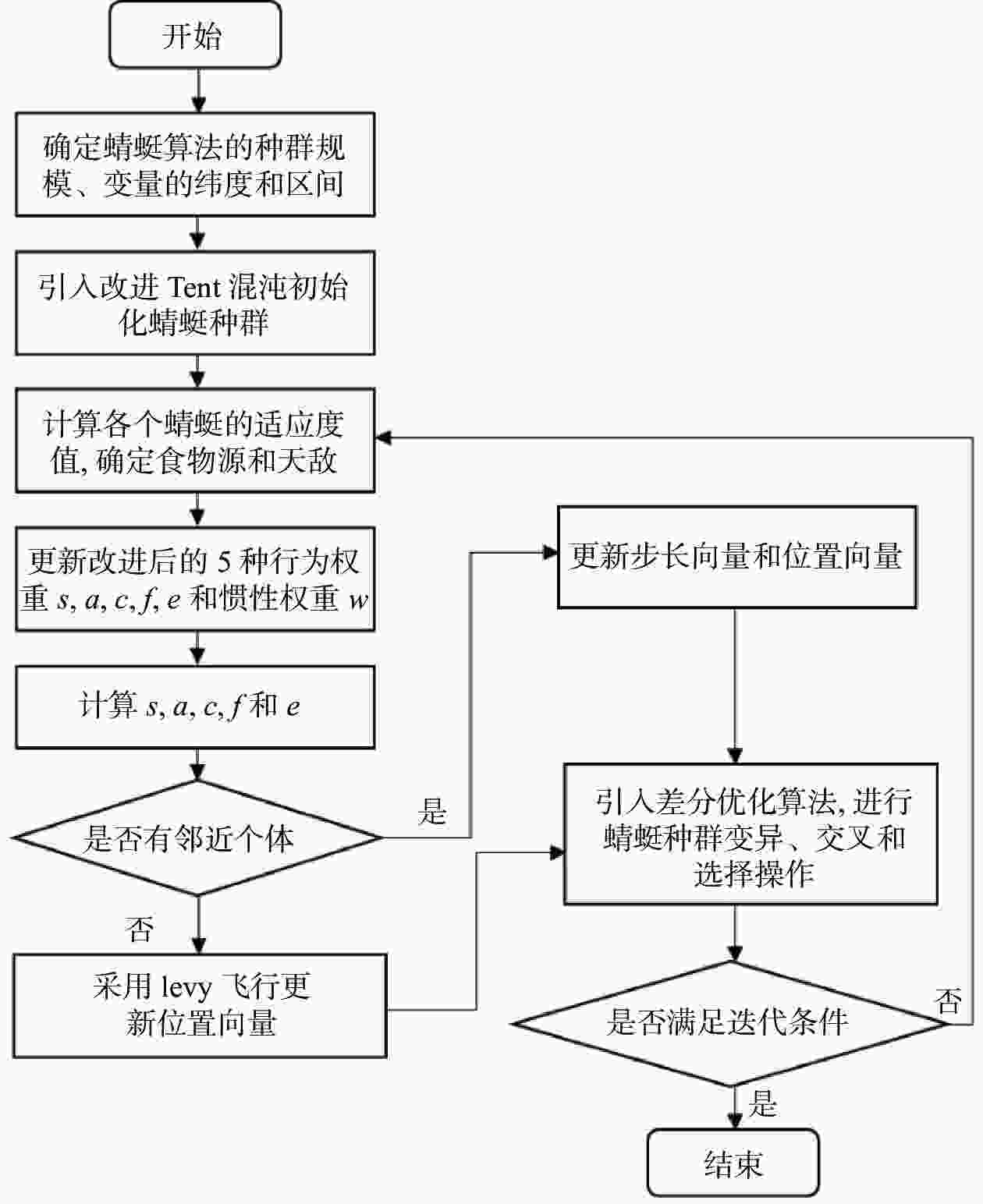
摘要: 针对蜻蜓算法初始种群随机性大、算法权重参数调节困难导致算法收敛精度低，后期种群收缩限制导致算法活力不足、收敛速度慢等问题，提出一种基于混沌映射和差分进化的改进蜻蜓算法。通过Tent混沌映射，使种群初始化分布均匀；改进对齐权重、聚集权重和惯性权重，提高收敛速度和精度；引入差分算法，提高最后时刻收敛速度；最终选取9个测试函数做仿真试验对比。结果表明，相较于基础蜻蜓算法、差分进化蜻蜓算法，基于混沌映射和差分进化改进后的蜻蜓算法收敛速度和精度提升显著，避免陷入局部最优解，能获得稳定可靠的全局最优解。Abstract: An improved dragonfly algorithm based on chaotic mapping and differential evolution was proposed to address several issues encountered in the original algorithm. The initial population’s significant randomness and the difficulty in adjusting algorithmic weight parameters led to low convergence accuracy. Additionally, later-stage population contraction restrictions resulted in decreased vitality and slow convergence speed. By employing Tent chaotic mapping, the population’s initial distribution was made more uniform. The alignment, clustering, and inertia weights were adjusted to enhance convergence speed and accuracy. The introduction of the differential evolution algorithm aimed to accelerate convergence at the final stages. Finally, nine test functions were selected for comparative simulation experiments. The results demonstrated that, compared to the basic dragonfly algorithm and the differential evolution dragonfly algorithm, the improved dragonfly algorithm based on chaotic mapping and differential evolution has significantly improved convergence speed and accuracy, avoiding getting stuck in local optima and obtaining stable and reliable global optimal solutions.
-
Key words:
- dragonfly algorithm /
- Tent chaotic mapping /
- weights /
- differential algorithm
-
图 3 改进前后惯性权重调整过程
Figure 3. Inertial weight adjustment process before and after improvement
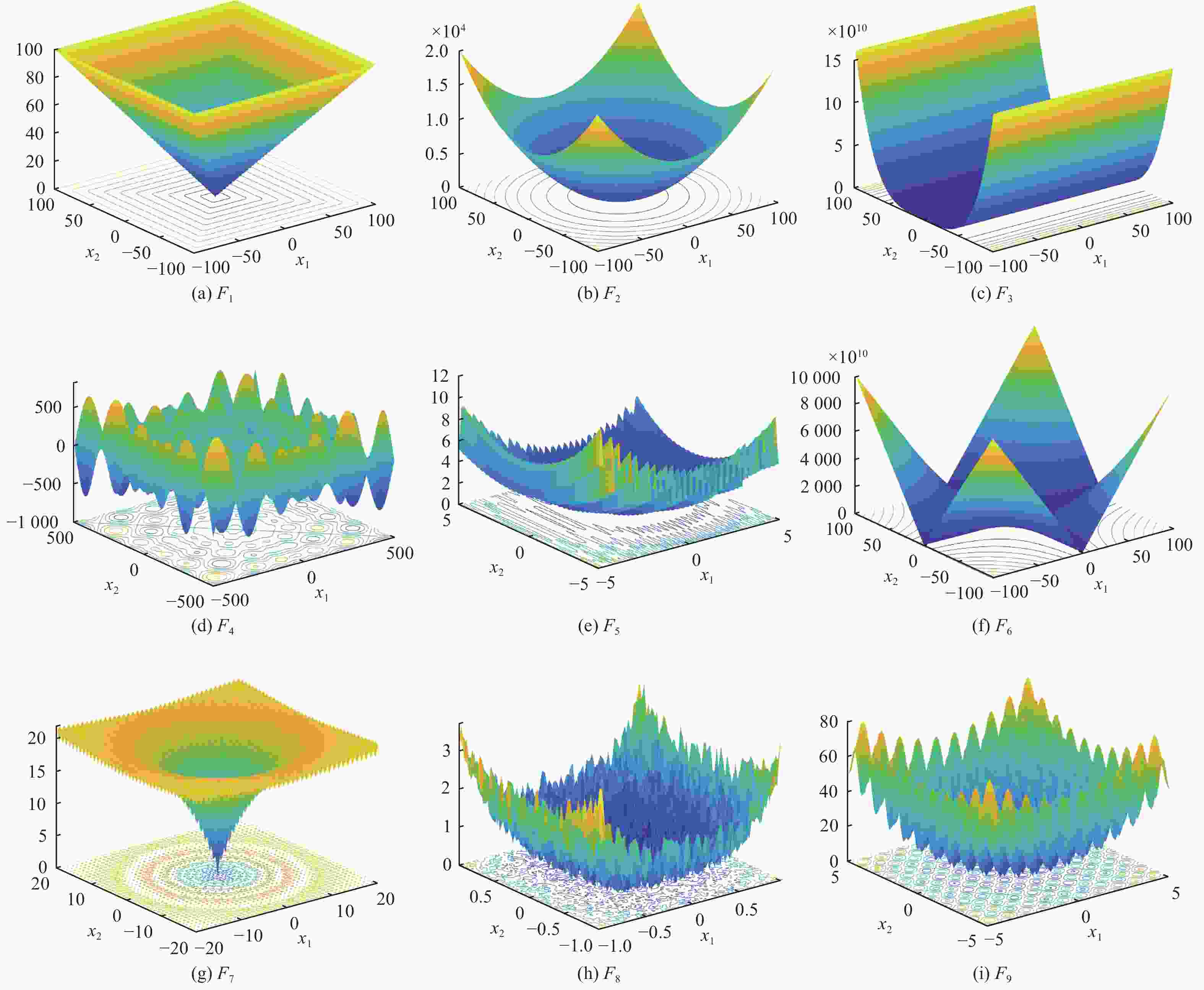
表 1 基准测试函数
Table 1. Benchmark function
测试函数 特点 维度 搜索范围 最优值 $ F_1^{}(x) = \mathop {\max }\limits_i \left\{ {\left| {{x_i}} \right|{\text{ , }}1 \leqslant i \leqslant 30} \right\}{\text{ }} $ 单峰 30 [−100, 100] 0 ${F_2} = 1 + \dfrac{1}{{4\;000}}\displaystyle\sum\limits_{i = 1}^D {x_i^2} - \prod\limits_{i = 1}^D {\cos } \left(\dfrac{{{x_i}}}{{\sqrt i }}\right)$ 单峰 30 [−600, 600]
0$ {F_3}\left( x \right) = \displaystyle\sum\limits_{i = 1}^{n - 1} {\left[ {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right]} $ 单峰 30 [−30, 30] 0 $ {F_4}(x) = \displaystyle\sum\limits_{i = 1}^n - {x_i}\sin (\sqrt {\mid {x_i}\mid } ) $ 单峰 30 [−500, 500] − 5100.400 $F_5^{}({x_i}) = {\left[ {\dfrac{1}{{500}}{\text{ + }}\displaystyle\sum\limits_{j = 1}^{25} {\dfrac{1}{{j + \displaystyle\sum\limits_{i = 1}^2 {{{({x_i} - {a_{ij}})}^6}} }}} } \right]^{ - 1}}$ 多峰 2 [−65.536, 65.536] 0 $ {F}_{6}\left(x\right) = {\displaystyle \sum _{i=1}^{n}\mid }{x}_{i}\mid + {\displaystyle \prod _{i=1}^{n}\mid }{x}_{i}\mid $ 多峰 30 [−10, 10] 0 $ F_7^{ }(x_i)=-20\exp\left(-0.2\sqrt{\dfrac{1}{30}\displaystyle\sum\limits_{i=1}^{30}x_i^2}\right)-\exp\left(\dfrac{1}{30}\displaystyle\sum\limits_{i=1}^{30}\cos2\text{π}x_i\right)+20+\mathrm{e} $ 多峰 30 [−32, 32] 0 $ F_8^{}({x_i}) = \displaystyle\sum\limits_{i = 1}^{30} {ix_i^4} + {\mathrm{random}}\left[ {0,1} \right){\text{ }} $ 多峰 30 [−1.28, 1.28] 0 $ {F_9}\left( x \right) = \displaystyle\sum\limits_{i = 1}^n {\left[ {x_i^2 - 10\cos \left( {2{\text{π}} {x_i}} \right) + 10} \right]} $ 多峰 30 [−5.12, 5.12] 15.128 
下载: 导出CSV
表 2 测试函数实验结果对比
Table 2. Test function experimental results
函数 算法 最优值 最差值 平均值 标准差 DA 1.62E − 02 3.93E + 02 1.02E + 01 1.21E + 01 F1 DADE 0.09E − 02 1.12E + 02 0.31E − 01 0.43E − 01 IDA 0.02E − 05 0.32E − 03 0.07E − 04 0.13E − 04 DA 6.13E − 07 3.51E + 01 5.85E − 04 7.65E − 04 F2 DADE 7.26E − 03 1.28E − 00 2.39E − 02 4.31E − 02 IDA 4.27E − 05 5.12E + 01 3.88E − 03 6.87E − 03 DA 8.41E + 00 9.53E + 03 2.04E + 01 3.78E + 01 F3 DADE 2.79E + 00 7.51E + 02 1.85E + 01 2.34E + 01 IDA 3.57E − 02 2.75E + 01 5.37E + 00 6.75E + 00 DA −1.62E + 02 −5.00E + 02 −1.32E + 02 −1.45E + 02 F4 DADE −2.76E + 03 −3.21E + 03 −3.15E + 03 −2.76E + 03 IDA −6.36E + 03 −3.25E + 03 −5.10E + 03 −5.35E + 03 DA 2.25E − 04 4.35E + 01 1.80E − 02 2.15E − 02 F5 DADE 1.21E − 02 3.57E + 02 1.35E + 00 2.78E + 01 IDA 5.12E − 04 2.37E + 02 9.91E − 01 1.33E + 00 DA 3.89E − 06 8.95E + 02 3.41E − 01 7.03E − 01 F6 DADE 4.17E − 08 7.55E + 02 6.15E − 02 2.75E − 01 IDA 2.32E − 11 5.86E − 01 1.07E − 04 5.38E − 04 DA 5.76E − 06 6.58E + 01 2.20E − 01 3.58E − 01 F7 DADE 7.88E − 07 8.33E + 01 1.51E − 03 4.15E − 03 IDA 3.27E − 09 6.77E + 00 1.11E − 05 2.76E − 05 DA 6.95E − 07 7.89E + 02 1.18E + 00 3.25E + 00 F8 DADE 5.98E − 08 3.27E + 01 9.87E − 01 1.57E − 01 IDA 1.78E − 10 5.67E − 01 6.88E − 02 8.65E − 02 DA 4.31E + 01 8.65E + 02 6.92E + 01 9.14E + 01 F9 DADE 3.68E + 01 5.78E + 03 6.27E + 01 8.42E + 01 IDA 1.51E + 01 6.87E + 02 2.96E + 01 6.11E + 01
下载: 导出CSV
-
[1] 连静. 基于竞争算子和破坏算子的改进蜻蜓算法[D] . 长春: 吉林大学, 2023. [2] 赵齐辉, 杜兆宏, 刘升, 等. 差分进化的蜻蜓算法[J] . 微电子学与计算机, 2018, 35(7): 21. [3] 张娜, 赵泽丹, 包晓安, 等. 基于改进的Tent混沌万有引力搜索算法[J] . 控制与决策, 2020, 35(4): 893 − 900. [4] 高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J] . 石油地球物理勘探, 2021, 56(4): 745−757. [5] 林涛, 冯嘉冀, 赵伊. 基于精英策略与正弦余制机制的蜻蜓算法研究[J] . 微电子学与计算机, 2020, 37(9): 24−30. [6] 门雅范, 杨宗仁, 陈嫄玲. 基于改进模糊聚类并行蜻蜓算法的无人水面艇航迹规划[J] . 机械设计与制造,2023(1):101 − 106. [7] ZHOU Y L, WANG J Z, LU H Y, et al. Short-term wind power prediction optimized by multi-objective dragonfly algorithm based on variational mode decomposition[J] . Chaos, Solitons & Fractals , 2022, 157. DOI: 10.1016/j.chaos.2022.111982. [8] ZHAO J, ZHANG D, HE Q, et al. A hybrid-strategy-improved dragonfly algorithm for the parameter identification of an SDM[J] . Sustainability,2023,15(15):11791. doi: 10.3390/su151511791 [9] CHEN Y, GAO B, LU T, et al. A hybrid binary dragonfly algorithm with an adaptive directed differential operator for feature selection[J] . Remote Sensing,2023,15(16):3980. doi: 10.3390/rs15163980 [10] ALSHAMMARI G, ALSHAMMARI M, ALMURAYZIQ T S, et al. Hybrid phishing detection based on automated feature selection using the chaotic dragonfly algorithm[J] . Electronics,2023,12(13):2823. doi: 10.3390/electronics12132823 [11] TIAN H, TIAN C, YUAN C, et al. Dynamic operation optimization based on improved dynamic multi-objective dragonfly algorithm in continuous annealing process[J] . Journal of Industrial and Management Optimization,2023,19(8):6159 − 6181. doi: 10.3934/jimo.2022210 [12] GUO H, GU W, KHAYATNEZHAD M, et al. Parameter extraction of the SOFC mathematical model based on fractional order version of dragonfly algorithm[J] . International Journal of Hydrogen Energy,2022,47(57):24059 − 24068. doi: 10.1016/j.ijhydene.2022.05.190 -
下载:
点击查看大图
图(5) / 表(2)
计量
- 文章访问数: 11
- HTML全文浏览量: 7
- PDF下载量: 0
- 被引次数: 0
