Quantification and analysis of shared battery value in electric vehicle battery swap stations
-
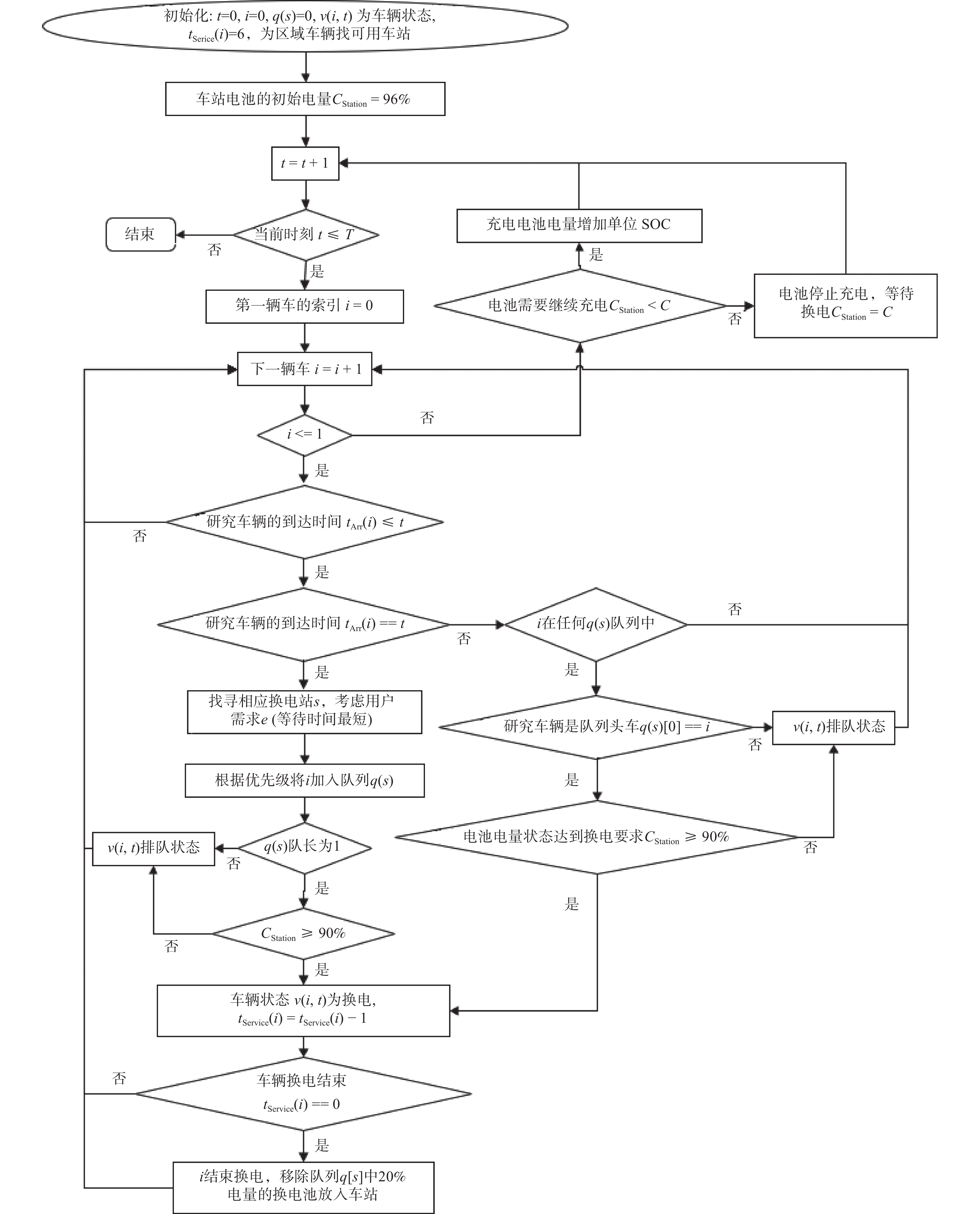
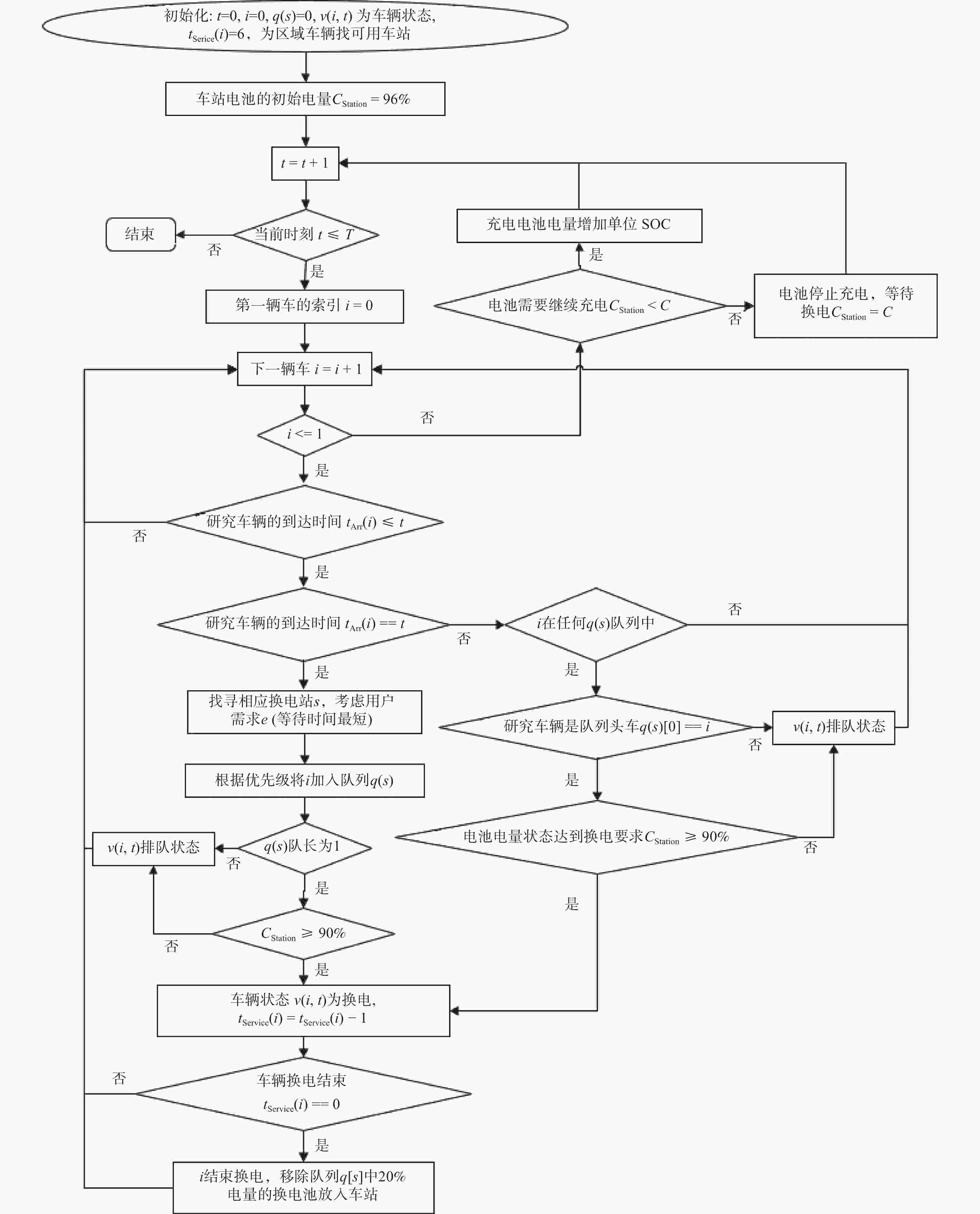
摘要: 多品牌电动汽车共享换电站已成为解决换电资源利用不足，运营成本投入大等问题的有效途径。提出一个模拟电动汽车选站、排队、换电及离开等行为的全流程仿真框架，重点研究换电站内不同品牌电池数量和电池共享模式对用户服务质量和运营成本的影响。基于蔚来汽车在上海换电网络中的换电站位置信息和运营数据开展多场景仿真，量化不同电池配置方案对换电用户等待时间的影响，以及维持用户等待时间在合理时间范围内所需的电池数量。仿真结果表明，合理配置换电站内电池数量或者采用多品牌电池共享方式，能够有效提高换电站服务质量，减少电池成本投入。Abstract: Multi-brandshared battery swap stations for electric vehicle have become an effective solution to address issues such as low utilization of battery swapping resources and high operational costs. A simulation framework was proposed to model the entire process of electric vehicle station selection, queuing, battery swapping, and departure behaviors, with a focus on investigating how battery quantities of different brands and battery-sharing models affect service quality and operational costs. Based on the location information and operational data of NIO's battery swapping network in Shanghai, multi-scenario simulations were conducted to quantify the impact of different battery configuration schemes on the queuing time for battery swapping users and to calculate the total number of batteries required to maintain a reasonable queuing time. The simulation results demonstrate that by optimizing the number of batteries in the swapping station or adopting a multi-brand battery sharing approach, the service quality of the swapping station can be significantly improved, and the cost of batteries can be reduced.
-
Key words:
- electric vehicle /
- battery swapping mode /
- battery ratio /
- battery sharing /
- numerical simulation
-
图 3 单位时间到达电动汽车数量分布
Figure 3. Distribution of electric vehicles arriving at station per unit time
图 5 不同电池配比方案对等待时间的影响
Figure 5. Impact of different battery ratio schemes on waiting time
图 6 对比共享换电站前后用户的平均等待时间
Figure 6. Comparison of average waiting time for users before and after shared car stations
图 7 多场景下不同电池配置方案对共享换电站数量的影响
Figure 7. Impact of different battery configuration schemes on the number of shared battery swap stations in multiple scenarios
图 8 电池共享与未共享对用户等待时间的影响
Figure 8. Impact of battery sharing vs. non-sharing on user waiting time
图 9 用户平均等待时间控制在10 min所需共享换电站数量
Figure 9. Number of shared battery swap stations required to control average user waiting time within 10 minutes
表 1 模型参数分析结果
Table 1. Analytic results of model parameters
场景 λ μ s Ls Lq Ws Wq M/M/1 6 8 1 3.00 2.25 30.0 22.50 M/M/2 12 8 2 2.68 1.93 13.4 9.65 
下载: 导出CSV
表 2 进站车辆仿真参数
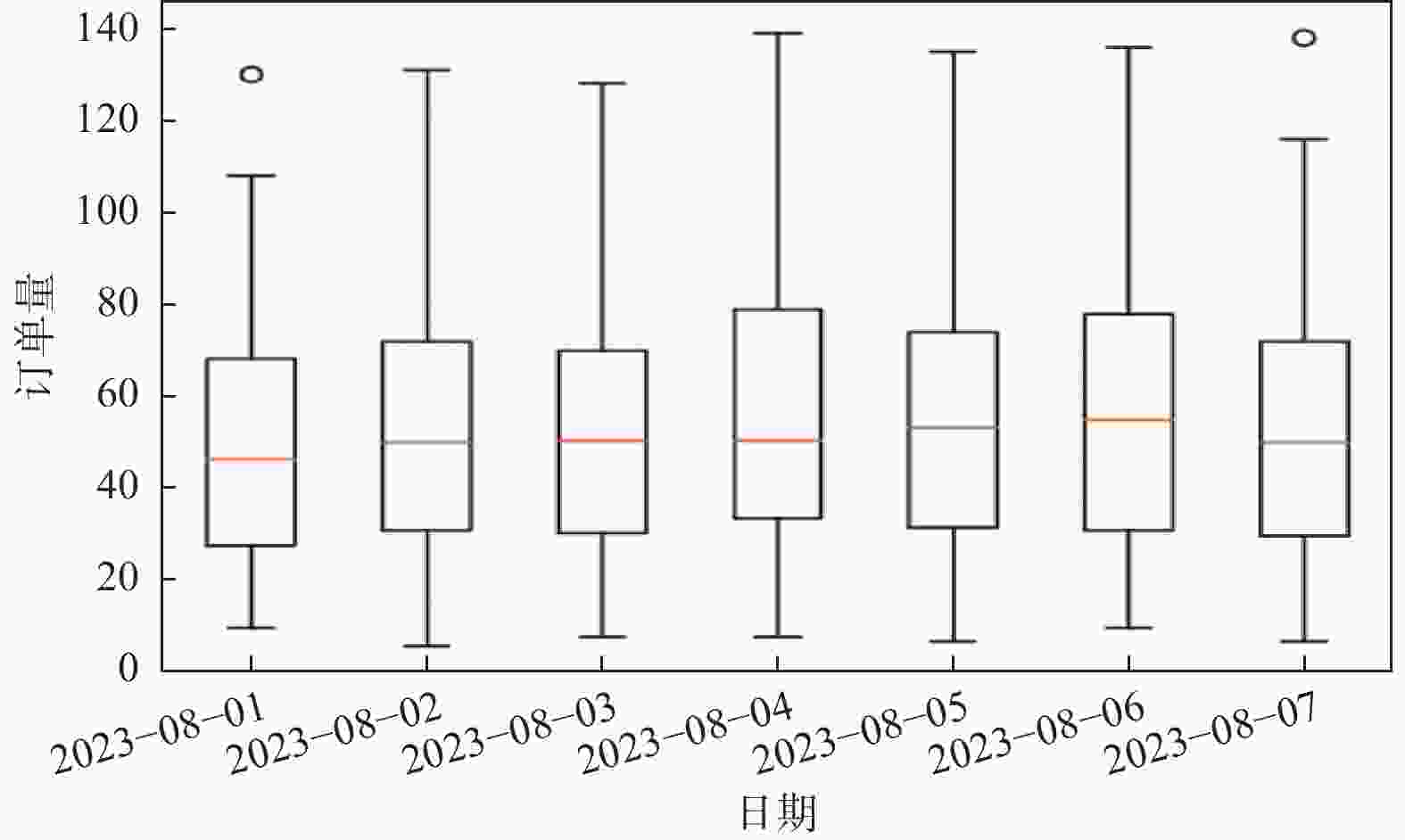
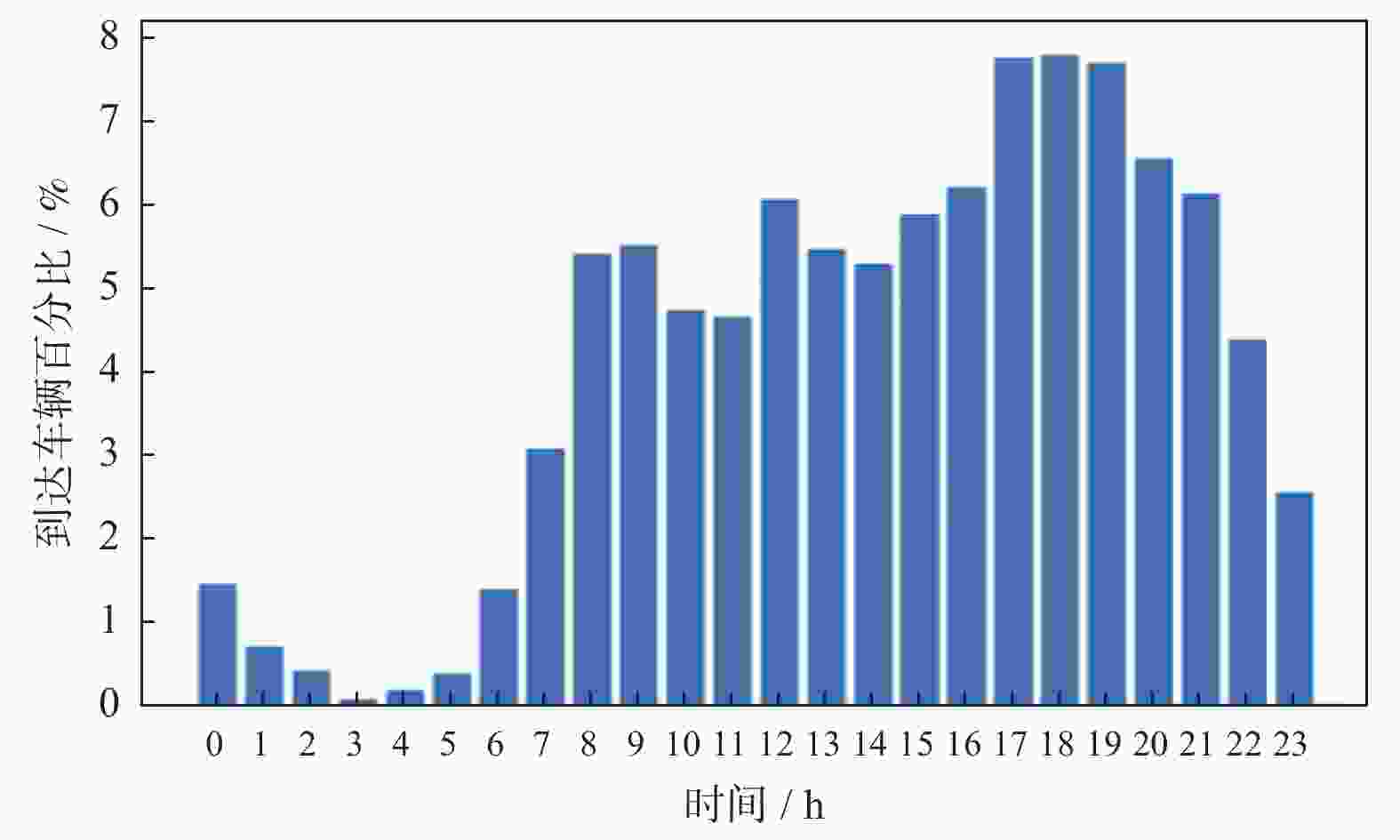
Table 2. Simulation parameters for incoming vehicles
属性 符号 说明 车辆索引 i 从i = 0开始 到达时间 tA 到达换电站的时间 初始电池容量(SOC) CArrive 到达换电站时的SOC 期望SOC CExp 期望离开时的SOC 电池容量 C 额定SOC 等待时间 tQueue 换电前的等待时间
下载: 导出CSV
表 3 换电站仿真参数
Table 3. Simulation parameters for battery swap station
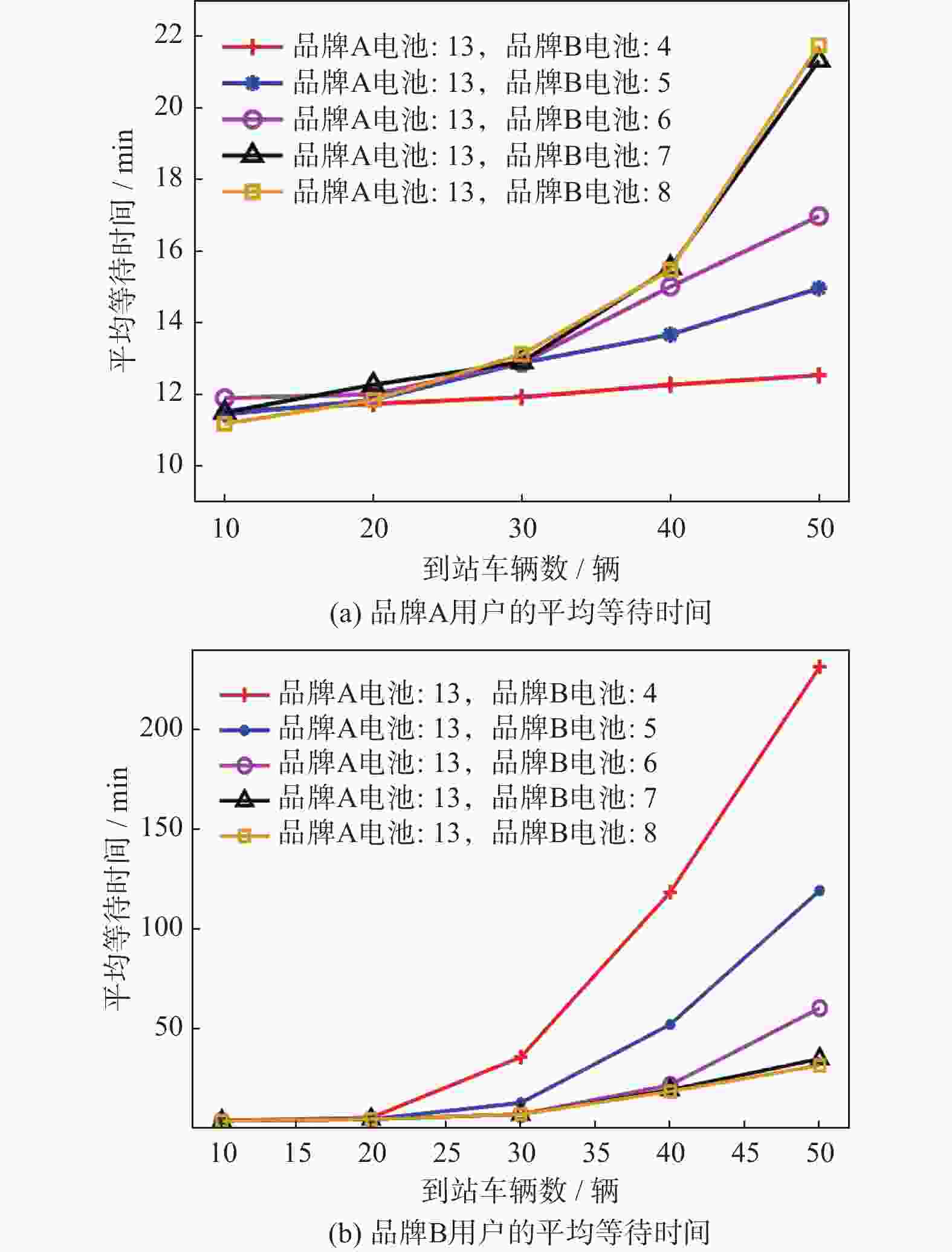
属性 符号 说明 换电站索引 s 从s = 0开始 站内队列 q 初始为一个空列表 当前SOC CStation 换电站初始SOC为96% 充电速率 △C 充电设备的功率决定 服务时间 tService 换电所需时间
下载: 导出CSV
表 4 电池配比对用户等待时间的影响
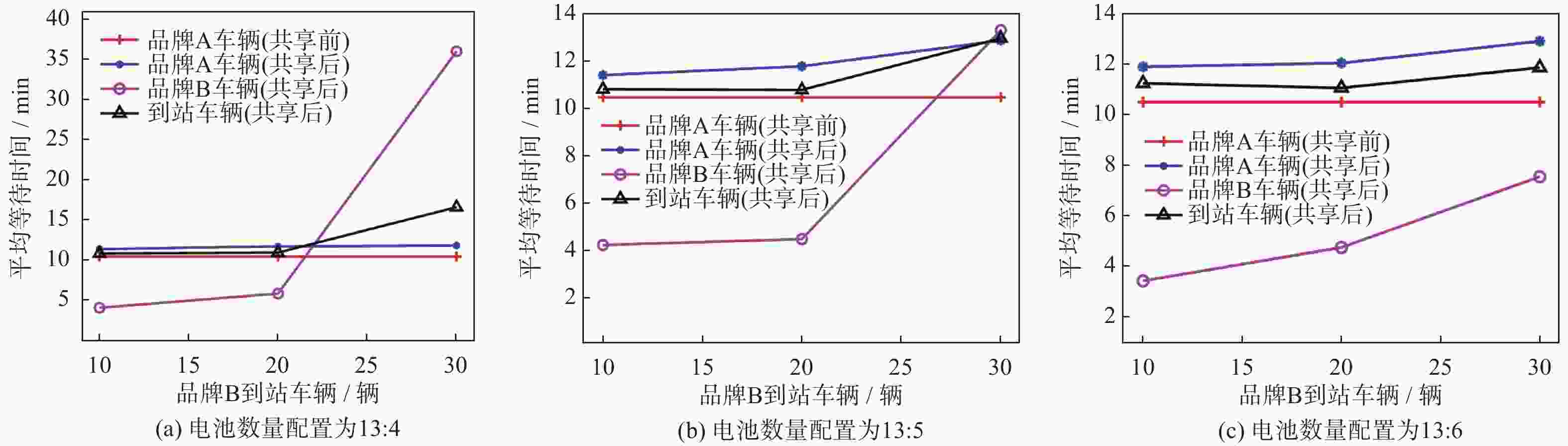
Table 4. Impact of battery ratio on user waiting time
电池配比 品牌用户平均
等待时间/min品牌B用户平均
等待时间/min所有用户平均
等待时间/minX=40, Y=4 12.1 28.0 14.7 X=40, Y=5 12.6 11.2 12.4 X=40, Y=6 12.8 7.3 11.9 X=40, Y=7 13.1 7.2 11.6 X=60, Y=4 12.6 48.0 20.6 X=60, Y=5 12.3 18.3 13.6 X=60, Y=7 13.3 8.2 12.2
下载: 导出CSV
-
[1] 崔杨, 李翼成, 付小标, 等. 基于换电服务定价策略及动态调控方法的含充换电站微电网系统双层优化调度[J] . 电网技术,2023,47(5):1998 − 2011. [2] 智研咨询. 2022年12月中国换电服务产业动态监测[EB/OL] . (2023-01-29)[2023-07-15] . https://www.chyxx.com/ku/1135124.html. [3] 吴婧, 刘霞. 电动汽车充电技术与换电技术浅析[J] . 汽车实用技术,2021,46(12):8 − 10. [4] 智研咨询. 2022年12月中国换电服务产业动态监测[EB/OL] . (2023−01−29)[2023−08−16] . https://www.chyxx.com/ku/1135124.html. [5] FRANK S, ULRICH W. T, DIEGO K. Optimization of battery charging and purchasing at electric vehicle battery swap stations[J] . Transportation Science,2018,52(5):1211 − 1234. doi: 10.1287/trsc.2017.0781 [6] MAK H Y, RONG Y, SHEN Z J M. Infrastructure planning for electric vehicles with battery swapping[J] . Management Science,2013,59(7):1557 − 1575. doi: 10.1287/mnsc.1120.1672 [7] 吕应龙. 基于遗传算法的电动公交车换电站选址模型[J] . 电工技术,2022(11):40 − 44, 47. [8] 张梅梅, 黄榆洁, 周梦迪, 等. 换电生态下换电站电池配置及经济性研究[J] . 工业技术经济,2022,41(9):18 − 25. doi: 10.3969/j.issn.1004-910X.2022.09.003 [9] 卢志平, 姚逸飞, 刘婷, 等. 换电站建设补贴对新能源汽车换电模式的影响: 基于供应链决策视角[J] . 供应链管理,2022,3(9):64 − 82. [10] 黄达. 基于改进式多种群遗传算法的换电服务调度优化方法[J] . 科技风,2022(6):58 − 62. [11] ZOU F Q, LIU N, LU X Y. Optimal configuration for battery switch stations of electric buses[C] // Proceedings of 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific). Piscataway: IEEE, 2014: 1−5. [12] 刘洪, 连恒辉, 葛少云, 等. 电动汽车换电站时序响应能力模型与充电计划制定策略[J] . 电力系统自动化,2017,41(8):91 − 97. doi: 10.7500/AEPS20160613005 [13] SCHNEIDER F, ULRICH W T. Optimization of battery charging and purchasing at electric vehicle battery swap stations[J] . Transportation Science, 2018, 52(5), 1211−1234. [14] HE Y Q, ZHANG Y J, FAN T, et al. The charging station and swapping station site selection with many-objective evolutionary algorithm[J] . Applied Intelligence, 2023, 53(1): 18041–18060. [15] 张昌华, 孟劲松, 曹永兴, 等. 换电模式下电动汽车换电充裕度模型及仿真研究[J] . 电网技术,2012,36(9):15 − 19. [16] WIDRICK R S, NURRE S G, ROBBINS M J. Optimal policies for the management of an electric vehicle battery swap station[J] . Transportation Science, 2018, 52(1): 59−79. [17] 周斯航, 康琦, 汪镭, 等. 基于换电运营模式的电动车电池充电策略研究[J] . 微型电脑应用,2019,35(2):9−12. doi: 10.3969/j.issn.1007-757X.2019.02.004 [18] BHAT U N. An introduction to queueing theory: modeling and analysis in applications[M] . New York: Springer, 2008: 141−161. [19] WIDRICK R S, NURRE S G, ROBBINS M J. Optimal policies for the management of an electric vehicle battery swap station[J] . Transportation Science,2018,52(1):59 − 79. doi: 10.1287/trsc.2016.0676 [20] ZHANG T Y, CHEN X, YU Z, et al. A monte carlo simulation approach to evaluate service capacities of EV charging ang battery swapping stations[J] . IEEE Transactions on Industrial Informatics,2018,14(9):3914 − 3923. doi: 10.1109/TII.2018.2796498 [21] LIU H, ZHANG Y, GE S. et al. Day-ahead scheduling for an electric vehicle pv-based battery swapping station considering the dual uncertainties[J] . IEEE Access,2019,7(8):115625 − 115636. [22] KOIRALA K, TAMAGN M. Planning and establishment of battery swapping station: a support for faster electric vehicle adoption[J] . Journal of Energy Storage,2022,51:104351. doi: 10.1016/j.est.2022.104351 -
下载:
点击查看大图
计量
- 文章访问数: 8
- HTML全文浏览量: 5
- PDF下载量: 1
- 被引次数: 0
