基于小波变换和L2正则化LSTM的股票价格预测

唐旋; 李路

doi:10.12299/jsues.24-0039

基于小波变换和L2正则化LSTM的股票价格预测

doi: 10.12299/jsues.24-0039

唐旋,
李路^,

上海工程技术大学数理与统计学院, 上海 201620

基金项目: 国家自然科学基金 (62173222)

详细信息

作者简介:
唐旋：唐　旋（1997 − ），女，硕士生，研究方向为深度学习、量化投资。E-mail：15705183237@163.com

通讯作者:
李　路（1968 − ），男，教授，博士，研究方向为机器学习、智能计算。E-mail：lilu@sues.edu.cn

中图分类号: TP391.1
计量
- 文章访问数: 10
- HTML全文浏览量: 5
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2024-02-28
- 刊出日期: 2025-05-19

Stock price prediction based on wavelet transform and L2-LSTM

TANG Xuan,
LI Lu^,

School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

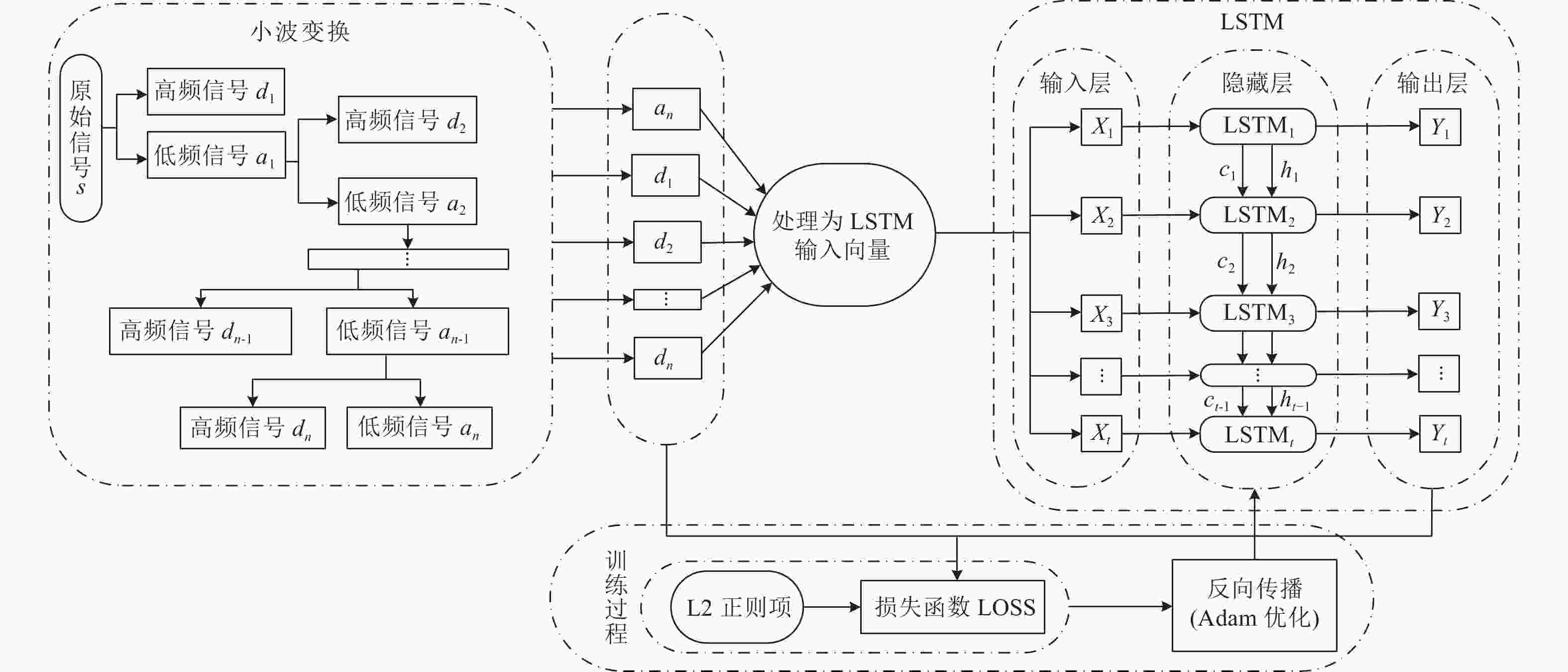
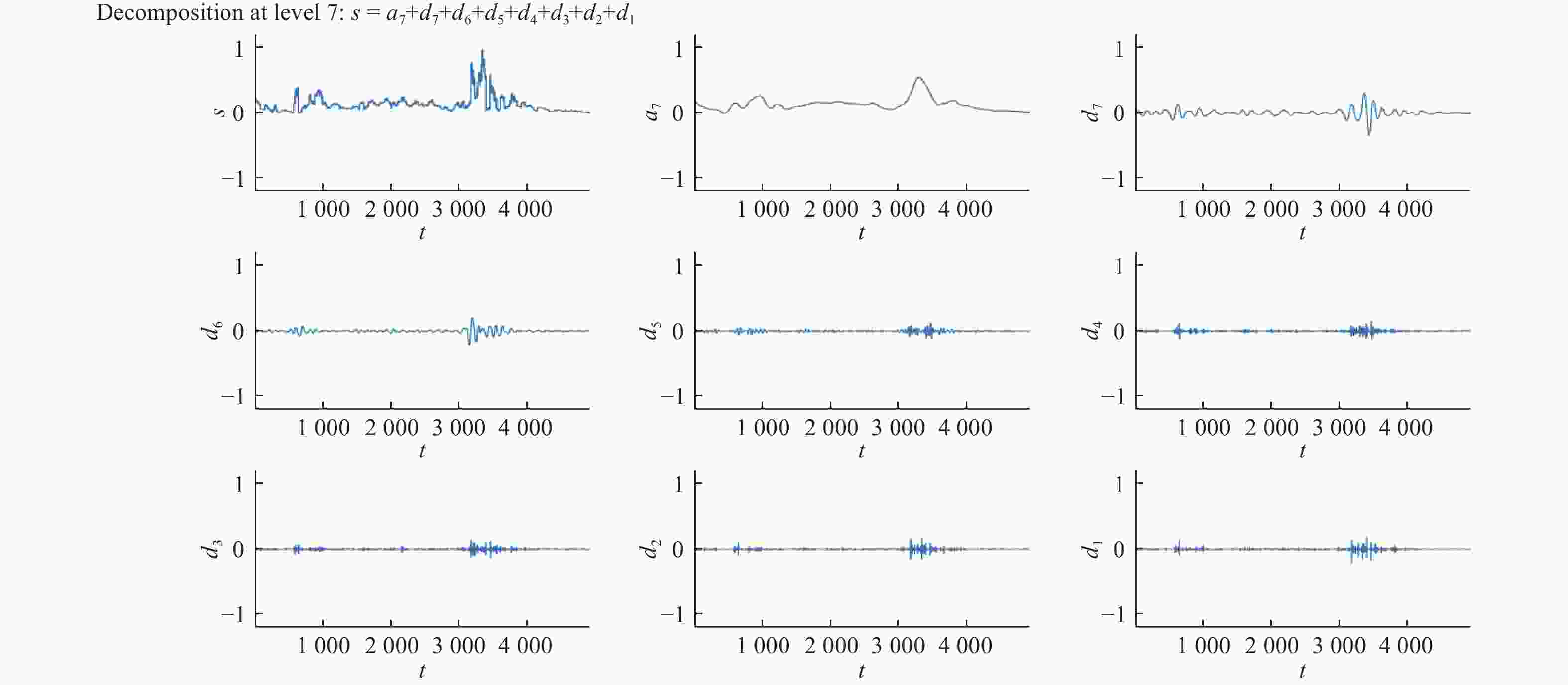
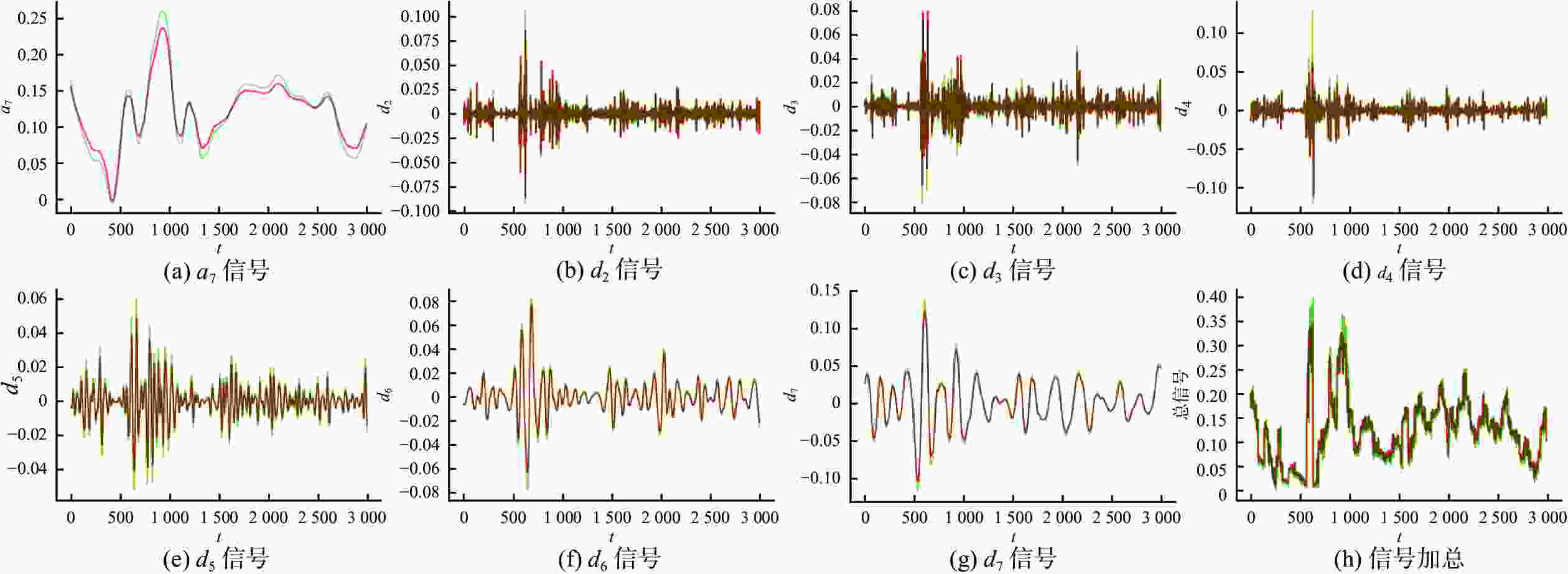
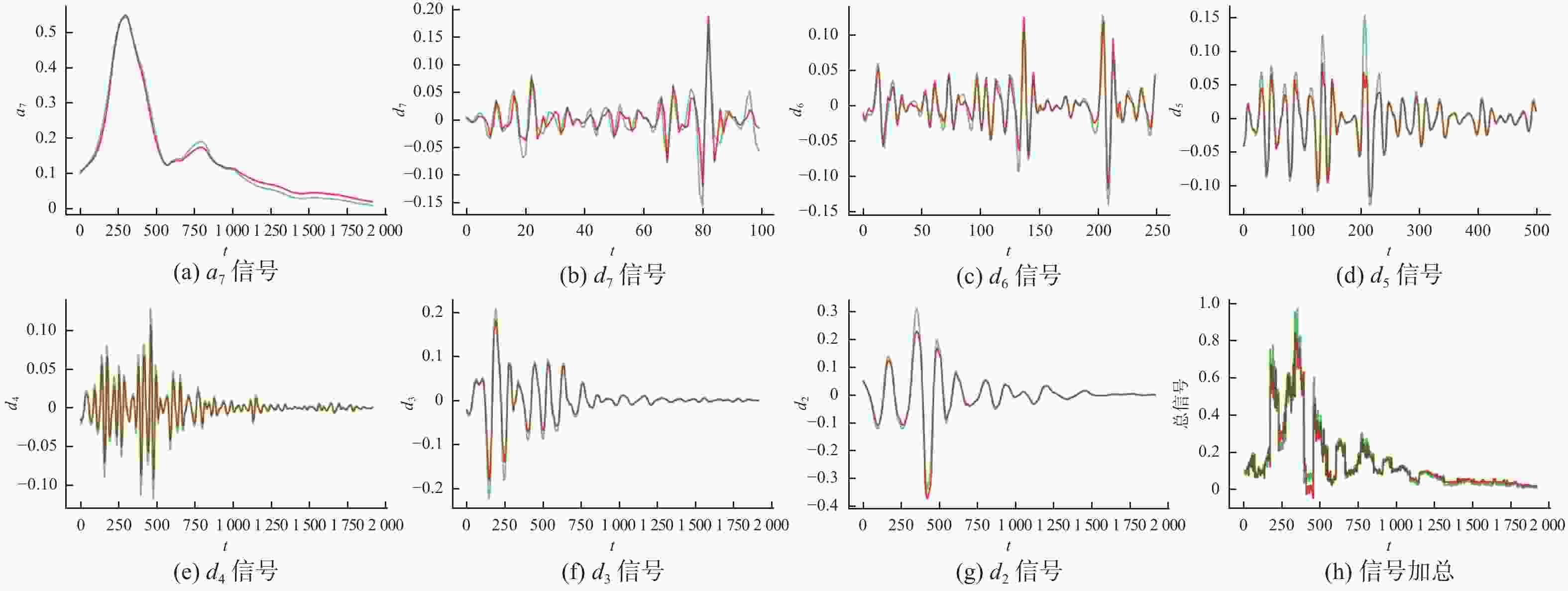
摘要: 长短时记忆网络(long short-term memory, LSTM)被广泛运用于股票的价格预测，但面对波动幅度较大的股票价格数据时，其预期效果不佳。提出一种基于小波变换和L2正则化LSTM的WT-L2-LSTM 模型，利用小波变换对原始宽频数据分解得到多层窄频数据，再逐层使用 L2正则化LSTM（L2-LSTM）模型进行预测，分解后数据较平滑且可以逐层调参。预测结果显示，WT-L2-LSTM模型在拟合优度和均方误差上均优于LSTM模型，表明WT-L2-LSTM模型对股价预测具有更好的精度和泛化性能。
- 股价预测 /
- 小波变换 /
- 长短时记忆网络 /
- L2正则化
Abstract: Long short-term memory (LSTM) networks are widely used for stock price prediction; however, their performance tends to be suboptimal when applied to stock price data with significant fluctuations. A novel WT-L2-LSTM model was proposed, which integrates wavelet transform with L2-LSTM. The original broadband data was decomposed into multiple layers of narrowband data using wavelet transform, and then the L2-LSTM model was used for the prediction layer by layer. The decomposed data is smoother and allows for parameter tuning layer by layer. The prediction results demonstrate that the WT-L2-LSTM model is superior to the LSTM model in terms of goodness of fit and mean square error, indicating that the WT-L2-LSTM model has better accuracy and generalization performance in predicting stock prices.
- stock price prediction /
- wavelet transform /
- long short-term memory (LSTM) /
- L2 regularization

HTML全文

图 1 经典LSTM单元结构

Figure 1. Classic LSTM structure

下载: 全尺寸图片幻灯片

图 2 模型结构

Figure 2. Model structure

下载: 全尺寸图片幻灯片

图 3 信号分解结果

Figure 3. Result of signal decomposition

下载: 全尺寸图片幻灯片

图 4 WT-L2-LSTM模型预测效果(训练集)

Figure 4. WT- L2-LSTM prediction effect (train)

下载: 全尺寸图片幻灯片

图 5 WT-L2-LSTM模型预测效果(测试集)

Figure 5. WT-L2-LSTM prediction effect(test)

下载: 全尺寸图片幻灯片

图 7 L2-LSTM模型预测效果

Figure 7. Prediction effect of L2-LSTM

下载: 全尺寸图片幻灯片

图 6 经典LSTM模型对原始信号预测效果

Figure 6. Prediction effect of classic LSTM on original signal

下载: 全尺寸图片幻灯片

表 1 L2-LSTM模型评价指标

Table 1. Evaluation indicators of L2-LSTM model

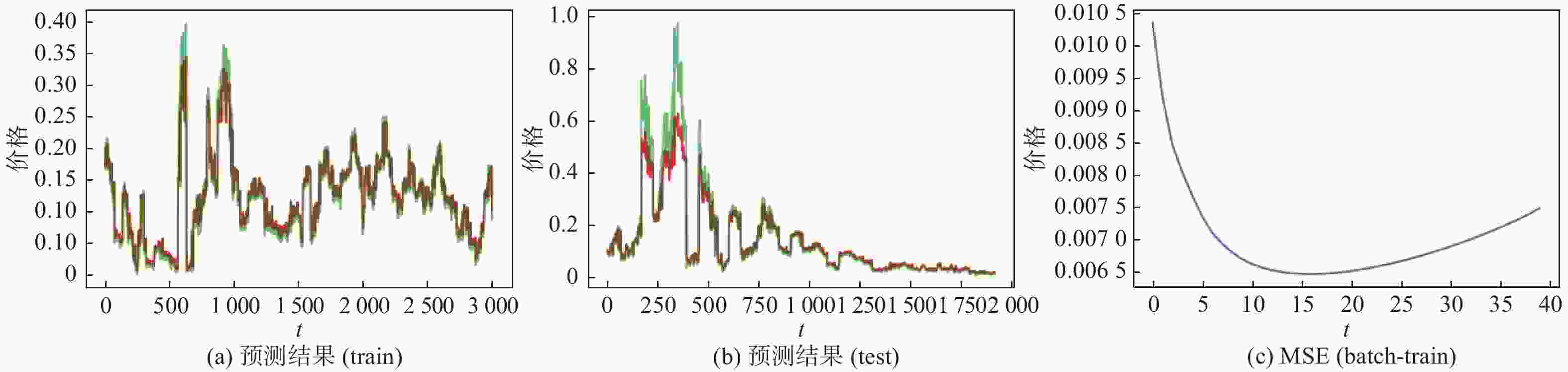
评价指标	数值	评价指标	数值
MSE(train)	0.0007	MSE(test)	0.0131
MAE(train)	0.0172	MAE(test)	0.0529
r²(train)	0.7133	r²(test)	−1.2078
RMSE(train)	0.0259	RMSE(test)	0.1145

下载: 导出CSV

表 2 WT-L2-LSTM模型评价指标

Table 2. Evaluation indicators of WT-L2-LSTM model

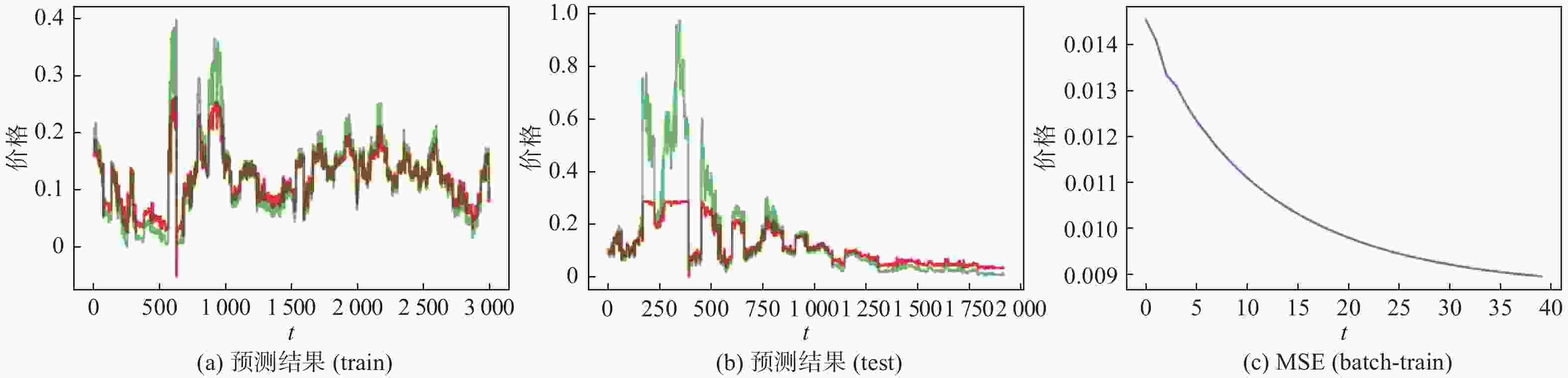
评价指标	数值	评价指标	数值
MSE(train)	0.0003	MSE(test)	0.0031
MAE(train)	0.0104	MAE(test)	0.0241
r²(train)	0.9244	r²(test)	0.8283
RMSE(train)	0.0174	RMSE(test)	0.0559

下载: 导出CSV

表 3 3次实验结果对比(测试集)

Table 3. Comparison of three experiments results (test)

模型	MSE	MAE	r²	RMSE
WT-L2-LSTM	0.0010	0.0192	0.9612	0.0319
L2-LSTM	0.0031	0.0241	0.8283	0.0559
LSTM	0.0131	0.0529	−1.2078	0.1145

下载: 导出CSV

参考文献(20)

[1]	贺毅岳, 高妮, 韩进博, 等. 基于长短记忆网络的指数量化择时研究[J] . 统计与决策,2020,36(23):128 − 133.
[2]	张妮. 基于LSTM 神经网络的股价预测应用研究[J] . 现代商业,2021(16):116 − 118.
[3]	林勇. 基于深度学习和网络大数据的金融时间序列分析及预测[D] . 成都: 四川师范大学, 2022.
[4]	周章元, 何小灵. 基于优化 LSTM 模型的股价预测方法[J] . 统计与决策,2023,39(6):143 − 148.
[5]	欧阳玉龙. 基于金融时间序列与深度神经网络的股票市场预测性研究[D] . 南昌: 江西财经大学, 2021.
[6]	乔泽东. 基于 WA-LSTM 的股指期货价格预测与择时策略研究[D] . 西安: 西北大学, 2021.
[7]	李美虹. 基于小波变换和神经网络的工业时序分析方法研究与应用 [D] . 沈阳: 中国科学院大学(中国科学院沈阳计算技术研究所), 2022.
[8]	魏光涛, 王泽黎, 张晓晨, 等. 基于小波分解和LSTM的夜经济电力商户分类模型研究[J] . 科技与创新,2023(3):122 − 125.
[9]	于博. 基于小波变换和卷积神经网络的时序分类方法研究[D] . 长春: 吉林大学, 2023.
[10]	李梦, 黄章杰, 徐健晖. 基于深度学习和小波分析的LSTM-Wavelet模型股价预测[J] . 重庆工商大学学报(自然科学版),2023,40(2):99 − 105.
[11]	任君, 王建华, 王传美, 等. 基于正则化 LSTM 模型的股票指数预测[J] . 计算机应用与软件,2018,35(4):44 − 48, 108. doi: 10.3969/j.issn.1000-386x.2018.04.008
[12]	BALAJI E, BRINDHA D, VINODH KUMAR E L, et al. Automatic and non-invasive Parkinson’s dis-ease diagnosis and severity rating using LSTM net-work[J] . Applied Soft Computing,2021, 108: 107463.
[13]	徐宝昌, 吕爽, 董秀娟, 等. 基于L2正则化LSTM 的非线性动态系统辨识[J] . 化工自动化及仪表,2021,48(1):1 − 7.
[14]	苏东月. 基于Lasso方法与LSTM的股票价格预测[D] . 北京: 华北电力大学, 2022.
[15]	宋旭东, 朱大杰, 杨杰, 等. 一种基于L2正则化迁移学习的变负载工况条件下故障诊断方法[J] . 大连交通大学学报,2022,43(2):106 − 109, 114.
[16]	黄培煜, 林雪, 谢镇涛, 等. 基于贝叶斯正则化LSTM模型的人均GDP预测效果: 以福建省为例[J] . 时代经贸,2023,20(6):140 − 144. doi: 10.3969/j.issn.1672-2949.2023.06.029
[17]	陈晓姨. 基于贝叶斯优化的CNN-LSTM股价预测模型[D] . 兰州: 兰州大学, 2023.
[18]	MORLET J, ARENS G, FORUTEAU E, et al. Wave propagation and sampling theory – part II: sampling theory and complex waves[J] . Geophysics,1982,47(2):222 − 236. doi: 10.1190/1.1441329
[19]	HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J] . Neural Computation,1997,9(8):1735 − 1780. doi: 10.1162/neco.1997.9.8.1735
[20]	HOERL A E, KENNARD R W. Ridge regression: biased estimation for nonorthogonal problems[J] . Technometrics,1970,12(1):55 − 67. doi: 10.1080/00401706.1970.10488634