基于神经网络的声学超材料板正反向设计方法

陈为谦; 郭辉; 傅伟; 孙裴; 王岩松

doi:10.12299/jsues.24-0163

基于神经网络的声学超材料板正反向设计方法

doi: 10.12299/jsues.24-0163

陈为谦^1,,
郭辉^1, ,,
傅伟²,
孙裴¹,
王岩松¹

1.
上海工程技术大学机械与汽车工程学院, 上海201620
2.
淄博市技师学院, 山东淄博 255000

基金项目: 国家自然科学基金(52172371)；上海市优秀学术/技术带头人计划项目（21XD1401100）；上海市新能源汽车振动噪声评价与控制技术专业服务平台（18DZ2295900）

详细信息

作者简介:
陈为谦（1997 − ），男，硕士生，研究方向为声学超材料板智能设计方法。E-mail：chenwq99@foxmail.com

通讯作者:
郭　辉（1981 − ），男，教授，博士，研究方向为振动噪声测控技术。E-mail：hgsues@163.com

中图分类号: TB535
计量
- 文章访问数: 14
- HTML全文浏览量: 10
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2024-06-07
- 网络出版日期: 2025-12-22
- 刊出日期: 2025-09-30

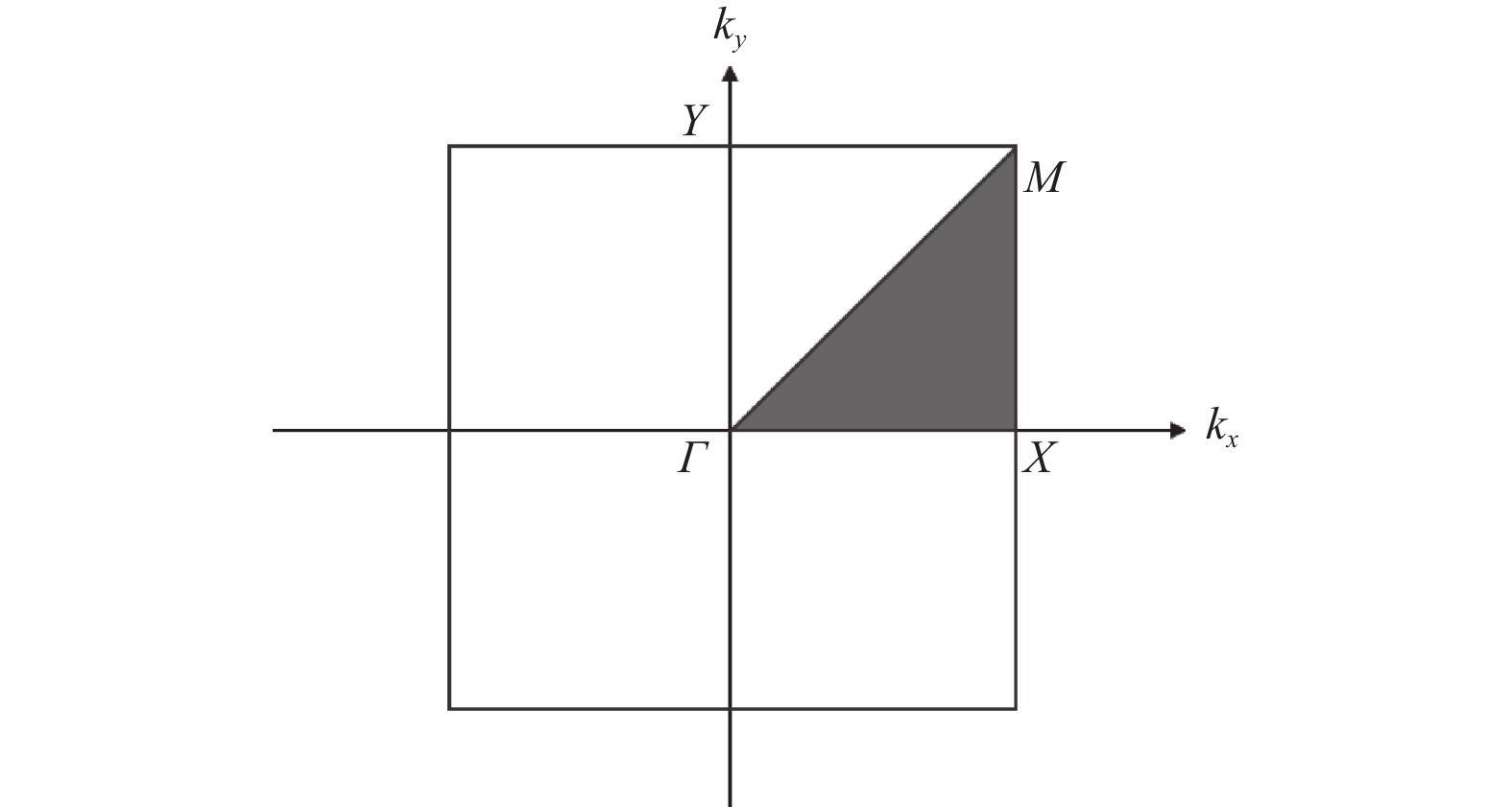
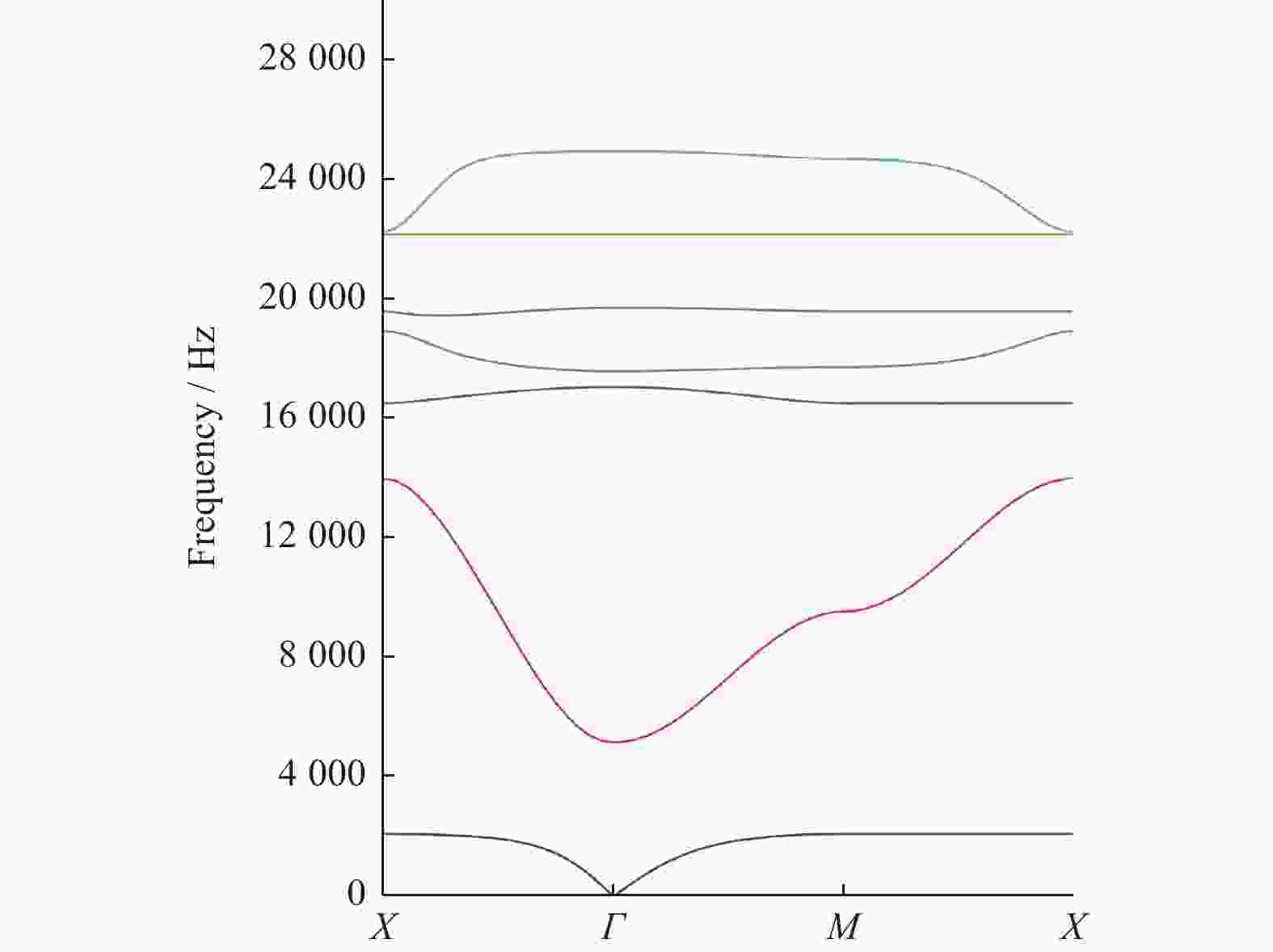
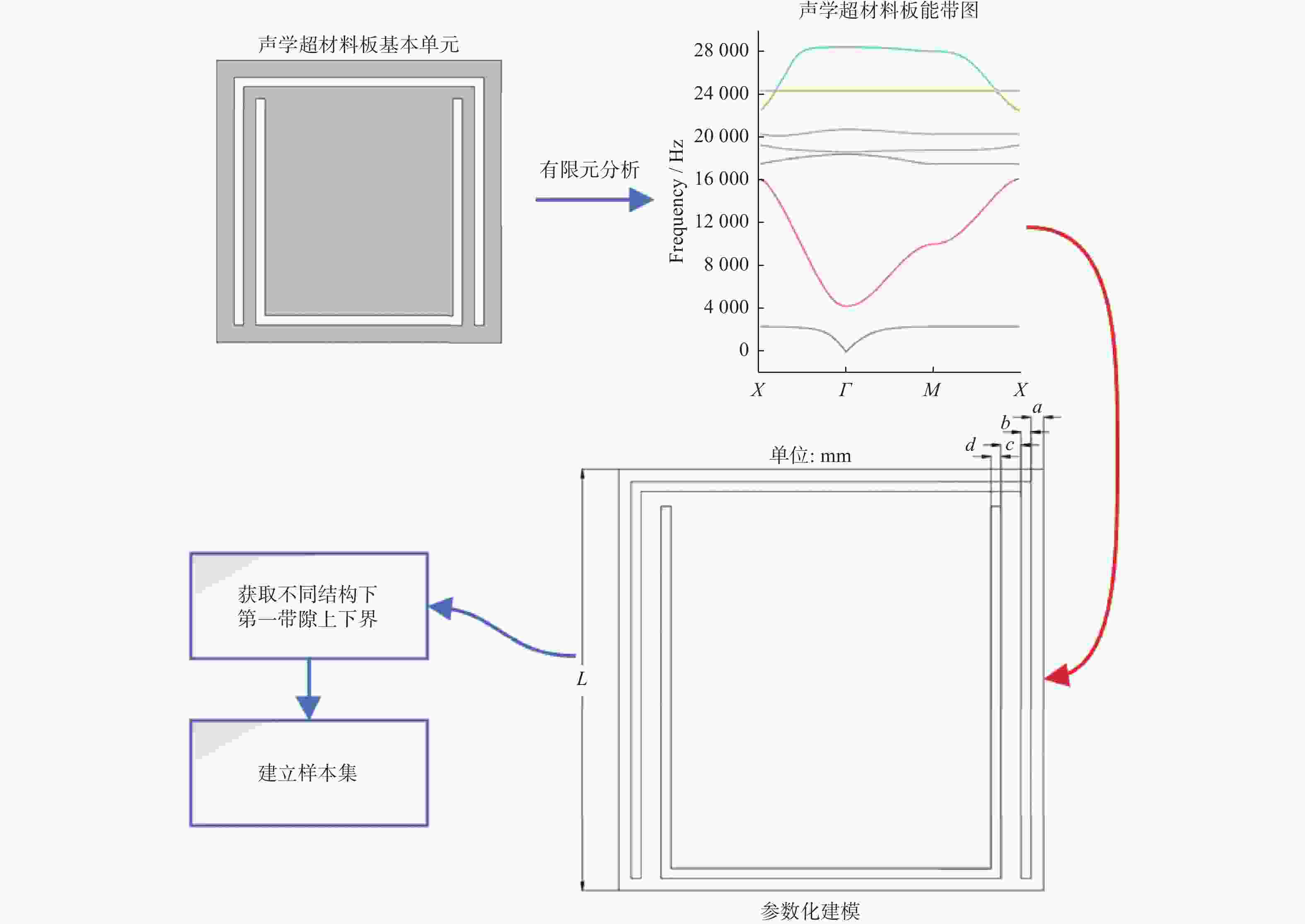
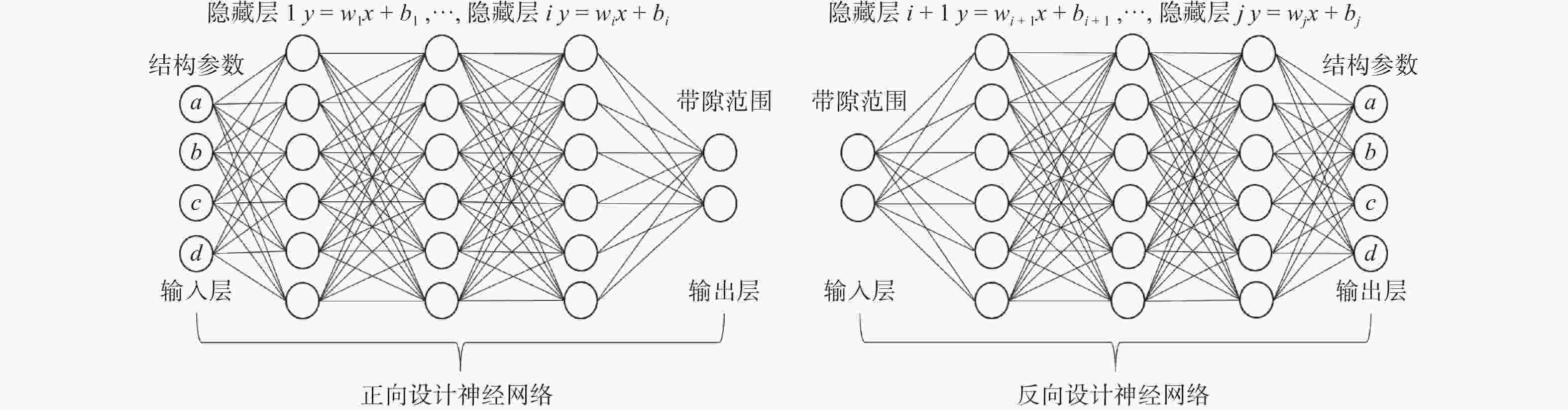
Forward-reverse design method for acoustic metamaterial plates based on neural networks

CHEN Weiqian^1
,,
GUO Hui^{1
, ,},
FU Wei²,
SUN Pei¹,
WANG Yansong¹

1.
School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China
2.
Zibo Technician College, Zibo 255000, China

摘要

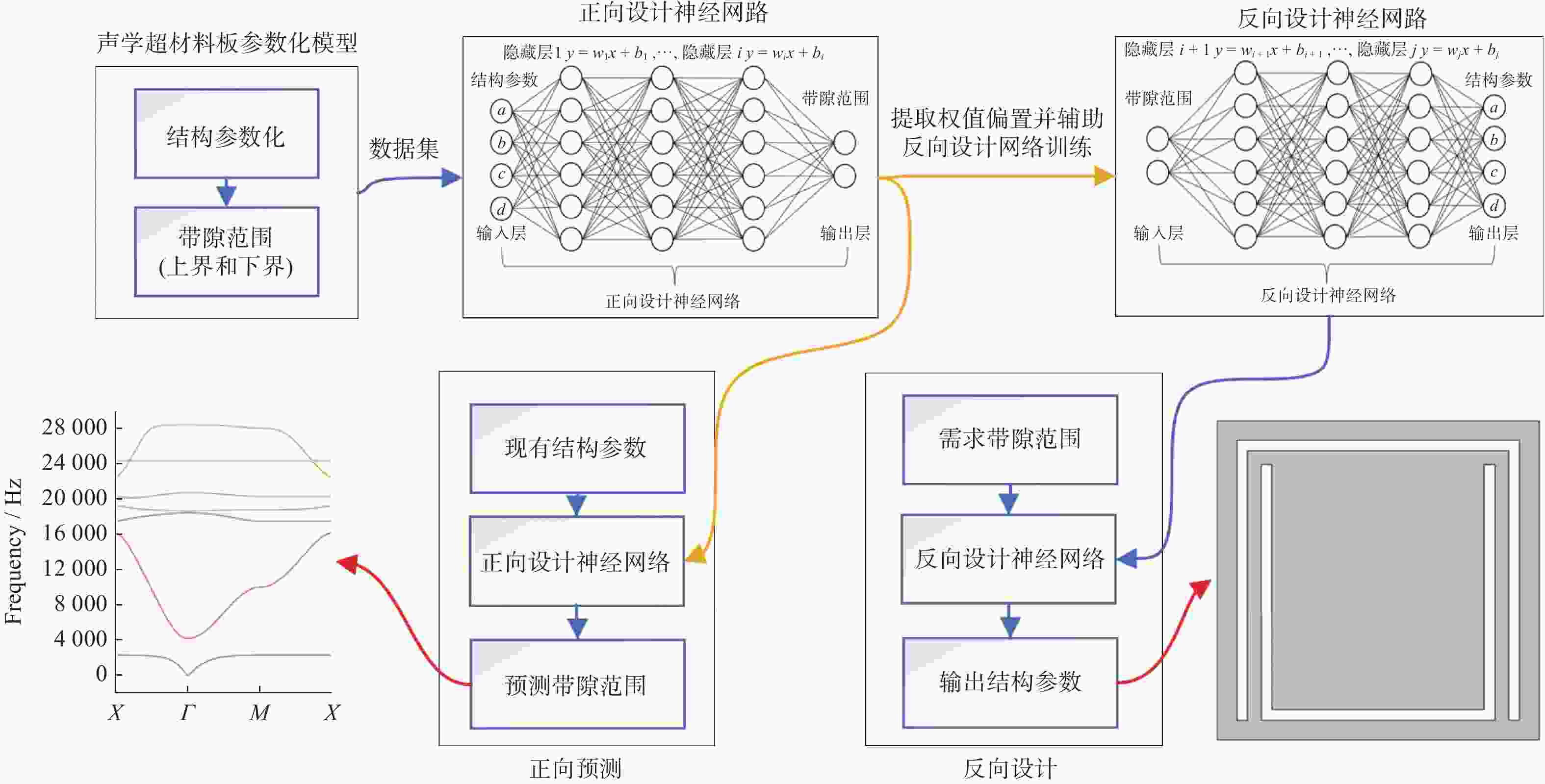
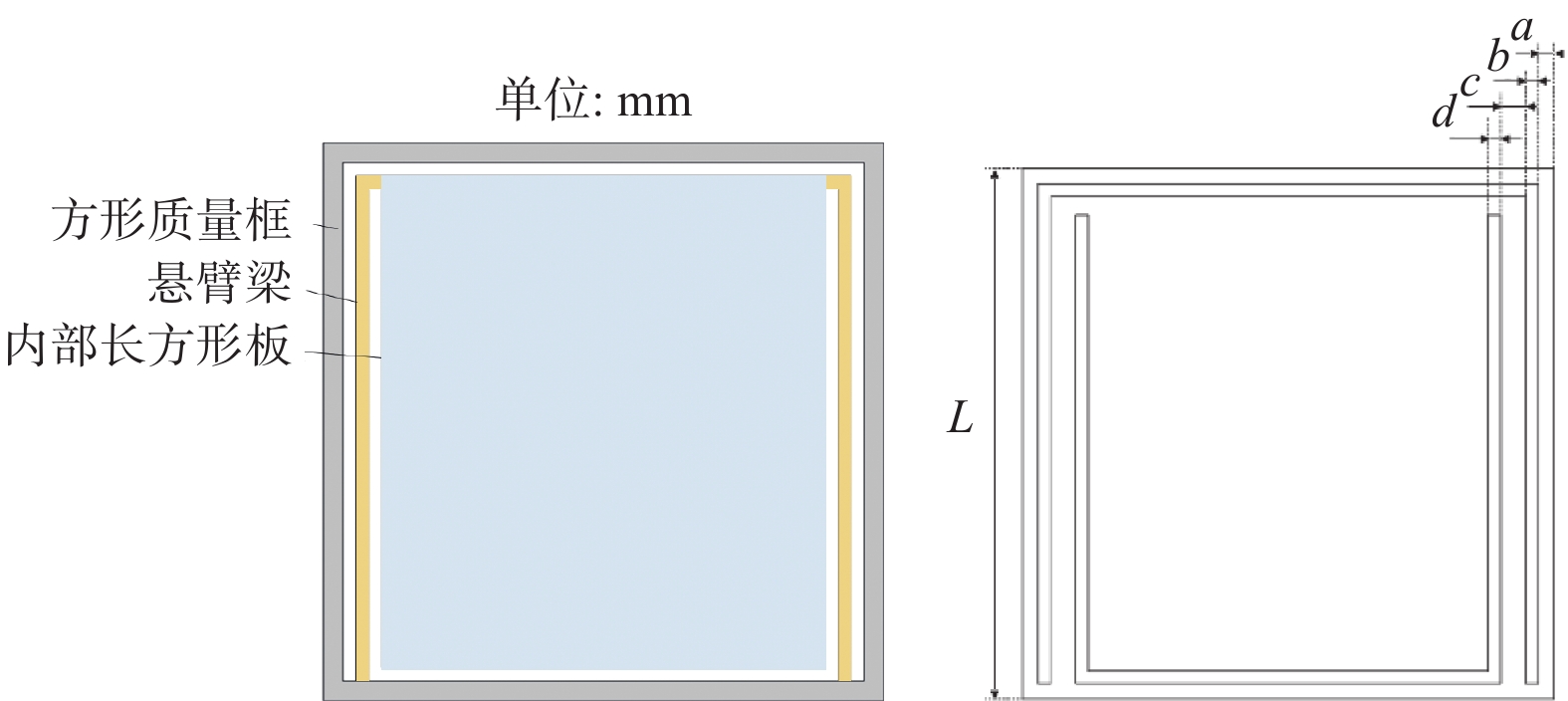
摘要: 声学超材料板是一种可以在特定频率范围内禁止弹性波传播的人工复合结构，由于存在多种机理的共同作用，其物理性能难以用理论公式进行推导和表述。设计一种基于局域共振机理的声学超材料板结构，利用有限元方法对其带隙特性进行分析，获得不同元胞结构参数及对应带隙特性，建立声学超材料板样本集。设计正向设计神经网络模型，获取结构参数与带隙范围的正向映射关系，实现输入结构参数即可输出相应的带隙范围的正向预测。在此基础上，提出一种反向设计神经网络模型，实现根据目标带隙范围获取声学超材料板结构参数的反向设计。仿真结果表明，提出的声学超材料板正反向设计方法可以避免复杂繁琐的理论推导和计算，有助于推动声学超材料领域的进一步发展。
- 声学超材料 /
- 带隙特性 /
- 有限元分析 /
- 神经网络模型 /
- 智能设计
Abstract: As an artificial composite structure, an acoustic metamaterial plate (AMP) can block the propagation of the elastic wave within specific frequency ranges. Due to the combined effects of multiple mechanisms in the composite structure, it is difficult to derive and express the physical properties using theoretical formulas. An AMP structure based on local resonance mechanism was proposed, and the bandgap characteristics were analyzed using finite element method, to obtain different cell structure parameters and corresponding bandgap characteristics. A sample set of the relationship between the structure parameters and corresponding bandgap characteristics was established for the AMP. A forward neural network model was designed to obtain the mapping relationship between structural parameters and bandgap range, and the forward prediction of the corresponding bandgap range by inputting structural parameters can be achieved. On this basis, a reverse neural network was proposed, and the reverse design can be carried out to obtain the structural parameters of AMP aiming the required bandgap range. The simulation results show that complex and cumbersome theoretical derivation and calculation can be avoided with the forward-reverse design method for AMP, which is helpful to promote further development of acoustic metamaterials.
- acoustic metamaterial /
- bandgap properties /
- finite element analysis /
- neural network model /
- intelligent design

HTML全文

图 1 声学超材料板基本单元

Figure 1. Unit of AMP

下载: 全尺寸图片幻灯片

图 2 正方形单元不可约布里渊区

Figure 2. Regular unit irreducible Brillouin zone

下载: 全尺寸图片幻灯片

图 3 声学超材料板基本单元能带图

Figure 3. Band diagram of AMP unit

下载: 全尺寸图片幻灯片

图 4 建立声学超材料板样本集流程图

Figure 4. Workflow of establishing sample set of acoustic metamaterial plates

下载: 全尺寸图片幻灯片

图 5 正反向设计神经网络示意图

Figure 5. Schematic diagram of forward-reverse neural network

下载: 全尺寸图片幻灯片

图 6 正反向设计神经网络的工作流程图

Figure 6. Workflow of forward and inverse design based on neural network

下载: 全尺寸图片幻灯片

表 1 声学超材料板材料参数

Table 1. Material parameters of AMP

参数	钢	空气
声速/(m·s⁻¹)	3300	343.2
泊松比	0.3	—
密度/( kg·m⁻³)	7700	1.2
杨氏模量/Pa	4.08×10¹⁰	—

下载: 导出CSV

表 2 数据集部分数据

Table 2. Part of data set

a/mm	b/mm	c/mm	d/mm	带隙上界/Hz	带隙下界/Hz
1.5	4.0	5.0	3.5	2359.763	6466.259
1.5	4.0	5.0	4.0	2380.481	6460.853
2.0	1.5	2.5	1.5	1590.832	4539.679
2.0	1.5	2.5	2.0	1602.459	4532.605
2.5	4.0	5.0	3.5	2498.582	5767.737
2.5	4.0	5.0	4.0	2521.416	5768.602
3.0	1.5	2.5	1.5	1655.130	4018.305
3.0	1.5	2.5	2.0	1667.593	4014.454

下载: 导出CSV

表 3 正向设计神经网络输出的带隙和有限元仿真带隙

Table 3. Band gaps from forward neural network model and finite element simulation

样本	a/mm	b/mm	c/mm	d/mm	正向设计神经网络输出/Hz	有限元仿真结果/Hz
1	3.12	1.56	2.33	3.37	3849~1657	3842~1665
2	1.73	3.27	3.32	2.69	5279~1950	5362~1911
3	2.64	2.43	3.62	1.29	4979~1975	4920~1995
4	2.25	3.75	3.75	2.15	5307~2079	5270~2084
5	1.86	1.77	2.61	2.79	4739~1690	4717~1657
6	3.69	2.21	1.51	3.15	3367~1421	3342~1386

下载: 导出CSV

表 4 反向设计神经网络计算结果

Table 4. Results of the reverse design neural network

目标带隙/Hz	a/mm	b/mm	c/mm	d/mm	仿真结果/Hz
1500~4500	2.28	3.21	2.56	3.19	1541.1~4461.3
1500~5000	1.15	0.72	2.44	4.81	1569.2~5110.6
2000~4500	3.74	3.16	3.27	3.31	2094.7~4440.9
2000~6000	1.61	3.08	3.95	2.35	2047.4~5895.0
2500~5000	3.65	1.97	4.69	3.13	2440.3~5045.2
2500~6000	1.58	3.84	4.96	4.25	2389.0~6075.1

下载: 导出CSV

参考文献(36)

[1]	IBRAHIM R A. Recent advances in nonlinear passive vibration isolators[J] . Journal of Sound and Vibration, 2008, 314(3/4/5): 371 − 452.
[2]	GRIPP J A B, RADE D A. Vibration and noise control using shunted piezoelectric transducers:a review[J] . Mechanical Systems and Signal Processing, 2018, 112: 359 − 383.
[3]	吴九汇, 马富银, 张思文, 等. 声学超材料在低频减振降噪中的应用评述[J] .机械工程学报, 2016, 52(13): 68 − 78.
[4]	CAI W S, CHETTIAR U K, KILDISHEV A V, et al. Optical cloaking with metamaterials[J] . Nature Photonics, 2007, 1(4): 224 − 227.
[5]	LU M H, FENG L, CHEN Y F. Phononic crystals and acoustic metamaterials[J] . Materials Today, 2009, 12(12): 34 − 42. doi: 10.1016/S1369-7021(09)70315-3
[6]	MA G C, SHENG P. Acoustic metamaterials: from local resonances to broad horizons[J] . Science Advances, 2016, 2(2): e1501595.
[7]	KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al. Acoustic band structure of periodic elastic composites[J] . Physical Review Letters, 1993, 71(13): 2022 − 2025. doi: 10.1103/PhysRevLett.71.2022
[8]	刘松, 罗春荣, 翟世龙, 等. 负质量密度声学超材料的反常多普勒效应[J] . 物理学报, 2017, 66(2): 208-212.
[9]	CROËNNE C, LEE E J S, HU H F, et al. Band gaps in phononic crystals: generation mechanisms and interaction effects[J] . AIP Advances, 2011, 1(4): 041401. doi: 10.1063/1.3675797
[10]	POPA B I, CUMMER S A. Non-reciprocal and highly nonlinear active acoustic metamaterials[J] . Nature Communications, 2014, 5(1): 3398. doi: 10.1038/ncomms4398
[11]	MALDOVAN M. Sound and heat revolutions in phononics[J] . Nature, 2013, 503(7475): 209 − 217.
[12]	温熙森, 温激泓, 郁殿龙, 等. 声子晶体[M] . 北京: 国防工业出版社, 2009.
[13]	LIU Z Y, ZHANG X X, MAO Y W, et al. Locally resonant sonic materials[J] . Science, 2000, 289(8): 1734 − 1736. doi: 10.1126/science.289.5485.1734
[14]	倪旭, 张小柳, 卢明辉, 等. 声子晶体和声学超构材料[J] . 物理, 2012, 41(10): 655 − 662.
[15]	柯满竹, 邱春印, 彭莎莎, 等. 声学超构材料[J] . 物理, 2012, 41(10): 663 − 668.
[16]	LANGFELDT F, KHATOKAR A J, GLEINE W. Plate-type acoustic metamaterials with integrated Helmholtz resonators[J] . Applied Acoustics, 2022, 199: 109019. doi: 10.1016/j.apacoust.2022.109019
[17]	YANG X H, KANG Y Z, XIE X X, et al. Multilayer coupled plate-type acoustic metamaterials for low-frequency broadband sound insulation[J] . Applied Acoustics, 2023, 209: 109399.
[18]	GAO W L, HU J X, QIN Z Y, et al. Flexural wave manipulation in perforated metamaterial plates with acoustic black holes interconnected by piezoelectric studs[J] . Composite Structures, 2023, 321: 117224. doi: 10.1016/j.compstruct.2023.117224
[19]	ANG L Y L, KOH Y K, LEE H P. Plate-type acoustic metamaterial with cavities coupled via an orifice for enhanced sound transmission loss[J] . Applied Physics Letters, 2018, 112(5): 051903. doi: 10.1063/1.5019602
[20]	YU D L, WEN J H, ZHAO H G, et al. Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid[J] . Journal of Sound and Vibration, 2008, 318(1/2): 193 − 205.
[21]	HOU Z L, ASSOUAR B M. Modeling of Lamb wave propagation in plate with two-dimensional phononic crystal layer coated on uniform substrate using plane-wave-expansion method[J] . Physics Letters A, 2008, 372(12): 2091 − 2097. doi: 10.1016/j.physleta.2007.10.080
[22]	KUSHWAHA M S, HALEVI P, MARTÍNEZ G, et al. Theory of acoustic band structure of periodic elastic composites[J] . Physical Review B, 1994, 49(4): 2313 − 2322. doi: 10.1103/PhysRevB.49.2313
[23]	TANAKA Y, TAMURA S I. Band structures of acoustic waves in phononic lattices[J] . Physica B: Condensed Matter, 2002, 316/317: 237 − 239. doi: 10.1016/S0921-4526(02)00473-8
[24]	GAUTHIER R C, MNAYMNEH K. Photonic band gap properties of 12-fold quasi-crystal determined through FDTD analysis[J] . Optics Express, 2005, 13(6): 1985 − 1998. doi: 10.1364/OPEX.13.001985
[25]	SAINIDOU R, STEFANOU N, PSAROBAS I E, et al. A layer-multiple-scattering method for phononic crystals and heterostructures of such[J] . Computer Physics Communications, 2005, 166(3): 197 − 240. doi: 10.1016/j.cpc.2004.11.004
[26]	KHELIF A, AOUBIZA B, MOHAMMADI S, et al. Complete band gaps in two-dimensional phononic crystal slabs[J] . Physical Review E, 2006, 74(4): 046610.
[27]	CHEN P Y, CHEN C H, WANG H, et al. Synthesis design of artificial magnetic metamaterials using a genetic algorithm[J] . Optics Express, 2008, 16(17): 12806 − 12818. doi: 10.1364/OE.16.012806
[28]	QIU T S, SHI X, WANG J F, et al. Deep learning: a rapid and efficient route to automatic metasurface design[J] . Advanced Science, 2019, 6(12): 1900128. doi: 10.1002/advs.201900128
[29]	WILT J K, YANG C, GU G X. Accelerating auxetic metamaterial design with deep learning[J] . Advanced Engineering Materials, 2020, 22(5): 2070018. doi: 10.1002/adem.202070018
[30]	HOU Z Y, ZHANG P Y, GE M F, et al. Metamaterial reverse multiple prediction method based on deep learning[J] . Nanomaterials, 2021, 11(10): 2672. doi: 10.3390/nano11102672
[31]	WANG H, XIAO S H, ZHANG C. Novel planar auxetic metamaterial perforated with orthogonally aligned oval-shaped holes and machine learning solutions[J] . Advanced Engineering Materials, 2021, 23(7): 2100102.
[32]	LI J, GUO H, SUN P, et al. Topology optimization of anisotropy hierarchical honeycomb acoustic metamaterials for extreme multi-broad band gaps[J] . Mechanics of Advanced Materials and Structures, 2023, 30(17): 3540 − 3552. doi: 10.1080/15376494.2022.2079027
[33]	LIAO Z Y, WANG Y J, GAO L, et al. Deep-learning-based isogeometric inverse design for tetra-chiral auxetics[J] . Composite Structures, 2022, 280: 114808.
[34]	KOLLMANN H T, ABUEIDDA D W, KORIC S, et al. Deep learning for topology optimization of 2D metamaterials[J] . Materials & Design, 2020, 196: 109098.
[35]	ZILETTI A, KUMAR D, SCHEFFLER M, et al. Insightful classification of crystal structures using deep learning[J] . Nature Communications, 2018, 9(1): 2775. doi: 10.1038/s41467-018-05169-6
[36]	贾高锋. 二维周期性结构带隙计算的有限元法[D] . 北京: 北京交通大学, 2009.