基于A*算法与螺旋线优化策略的堆高机自主作业路径规划

何维瀚; 崔国华; 卢声耀; 张若平

doi:10.12299/jsues.24-0166

基于A*算法与螺旋线优化策略的堆高机自主作业路径规划

doi: 10.12299/jsues.24-0166

上海工程技术大学机械与汽车工程学院, 上海 201620

基金项目: 国家自然科学基金（52372428）

详细信息

作者简介:
何维瀚（1996 − ），男，硕士生，研究方向为移动机器人路径规划。E-mail：1530614897@qq.com

通讯作者:
崔国华（1975 − ），男，教授，博士，研究方向为移动作业机器人、港口无人作业车辆等。E-mail：ghcui2018@sues.edu.cn

中图分类号: TP242
计量
- 文章访问数: 15
- HTML全文浏览量: 8
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2024-06-11
- 网络出版日期: 2026-02-02
- 刊出日期: 2025-12-01

Path planning for autonomous empty container handler based on A* algorithm and spiral curve optimization strategy

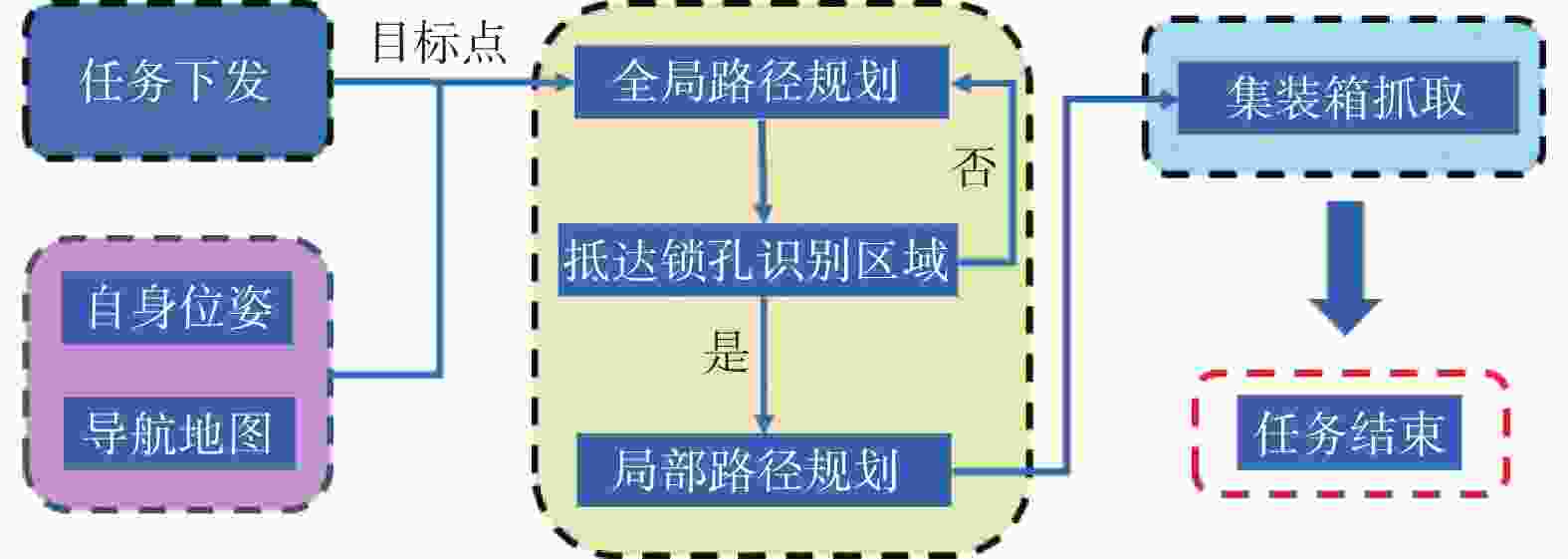
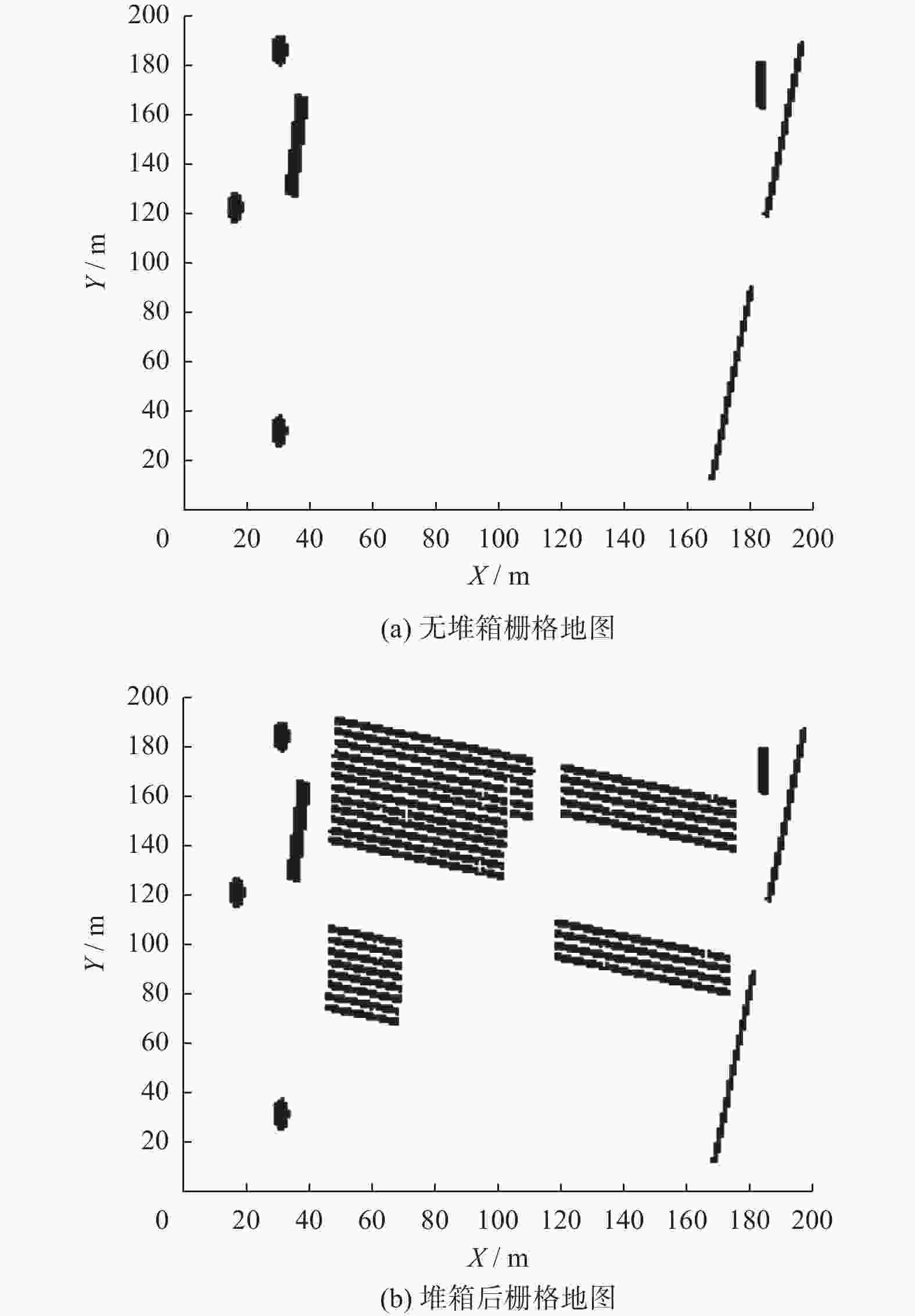
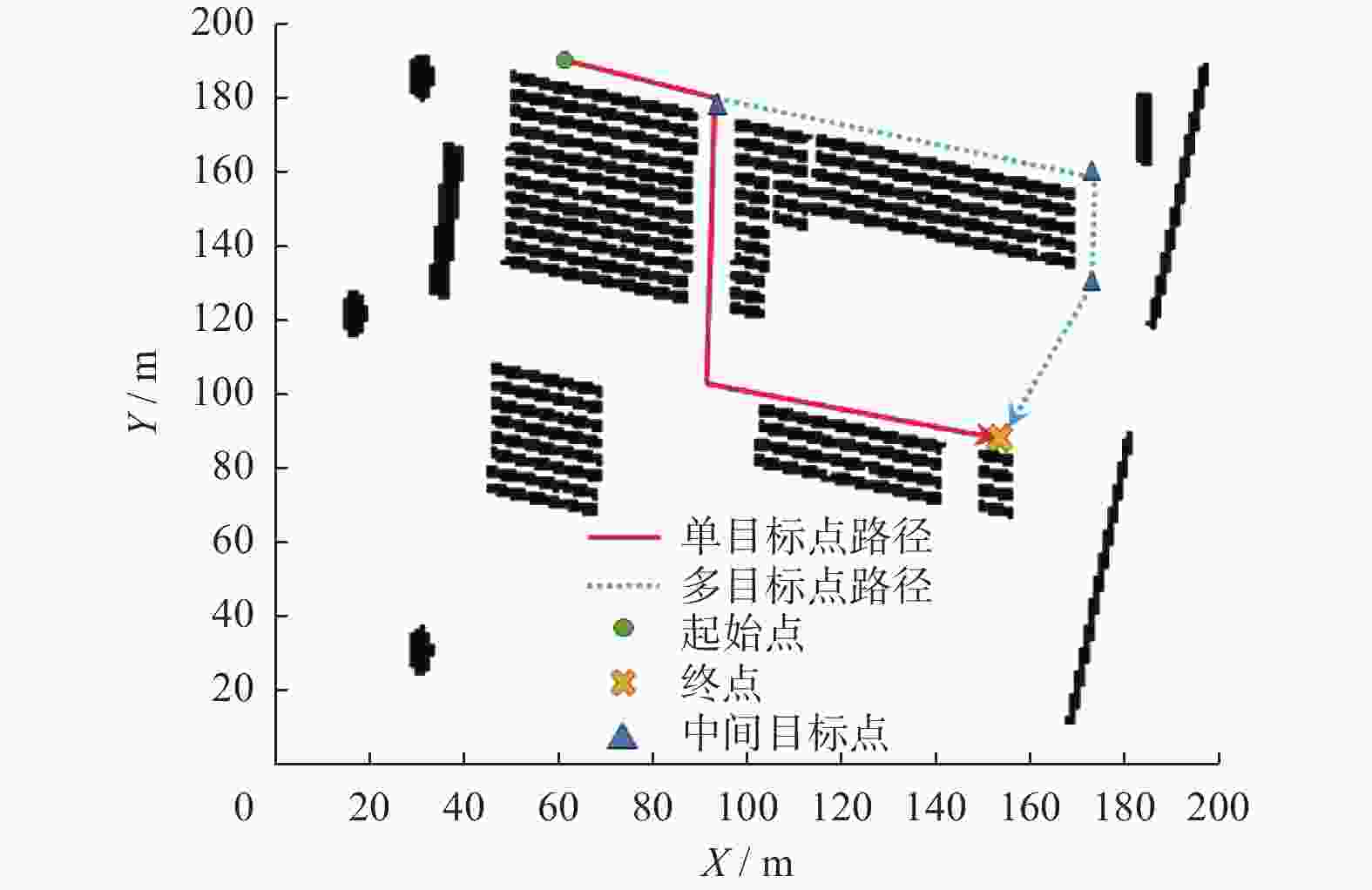
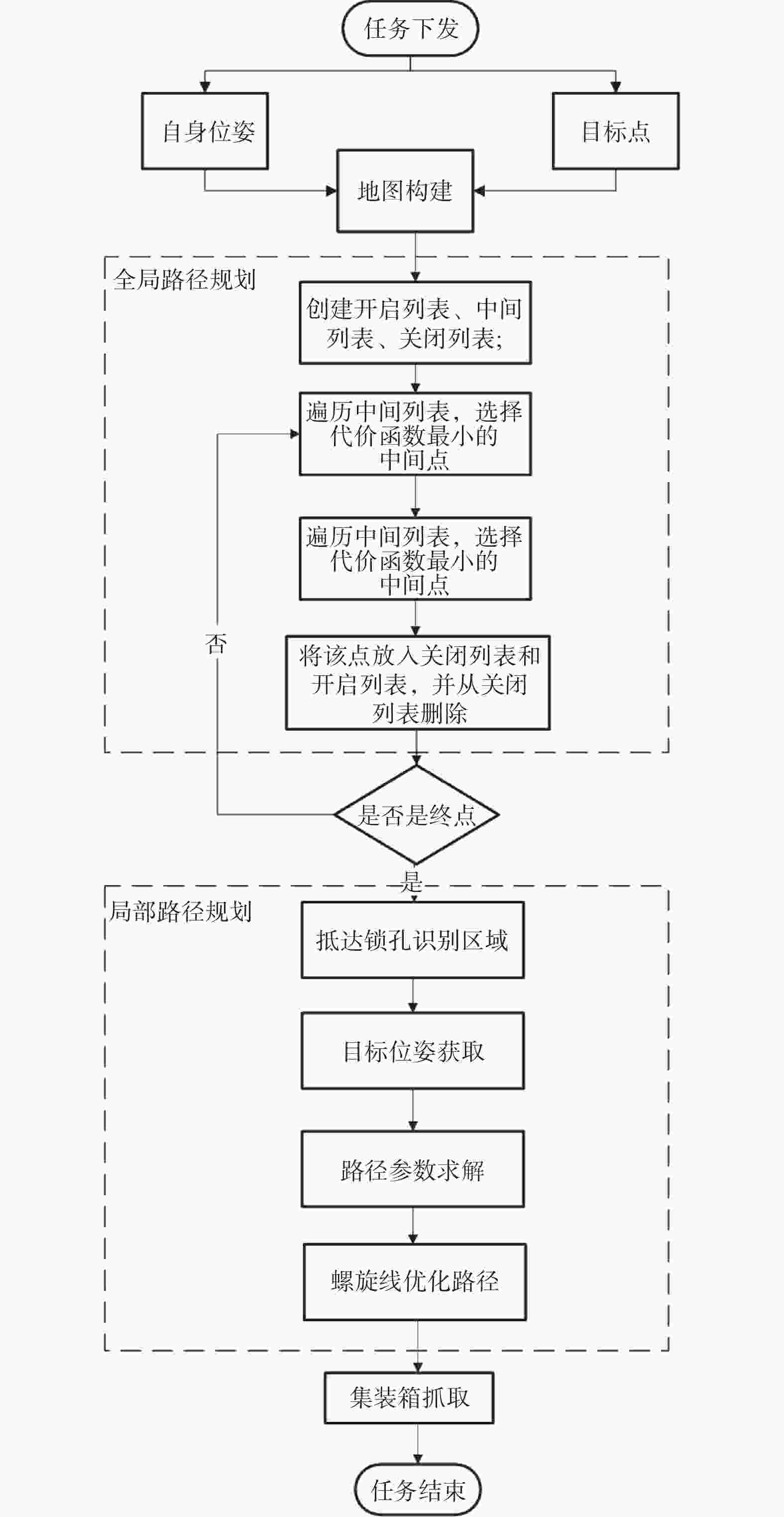
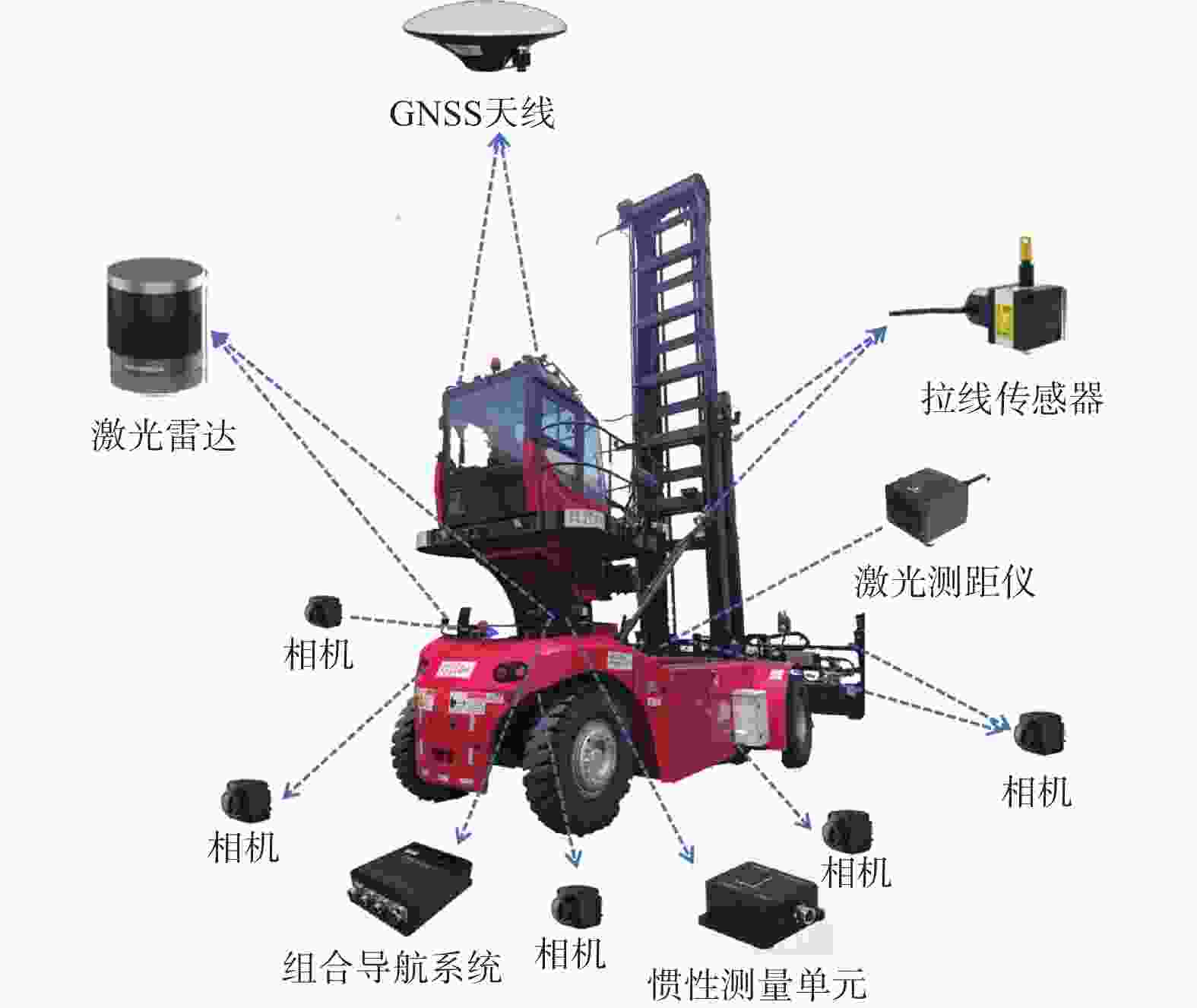
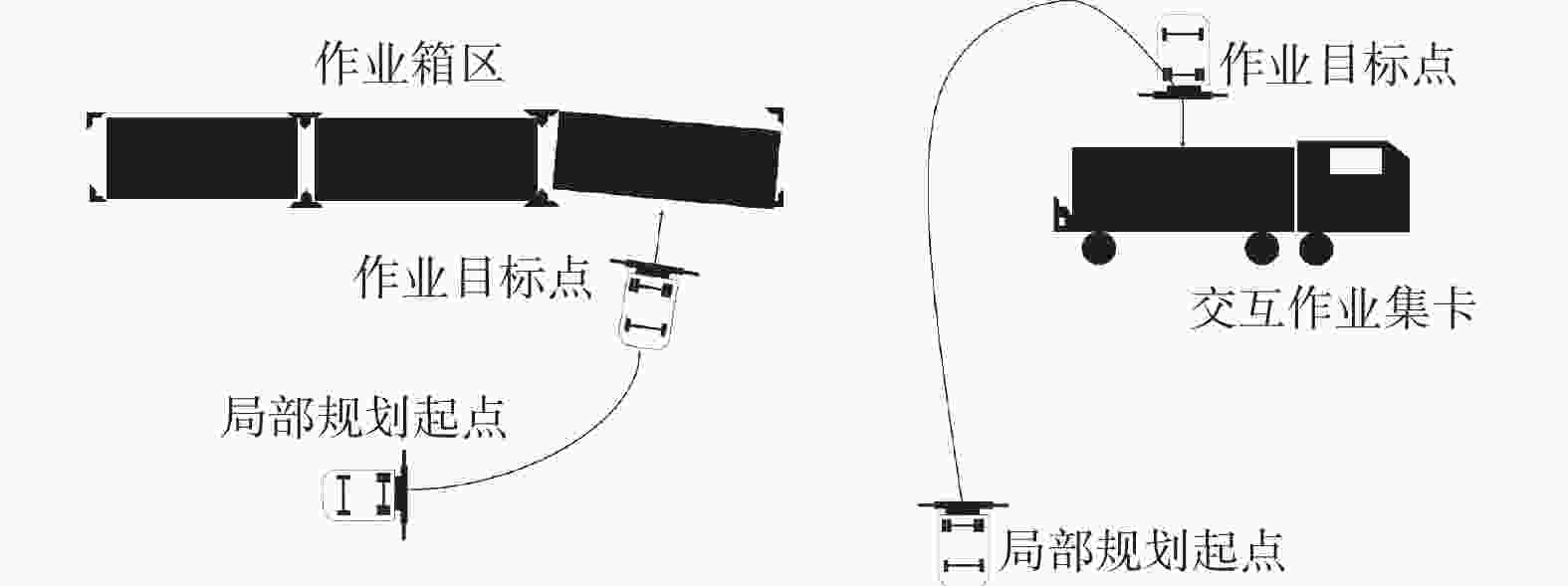
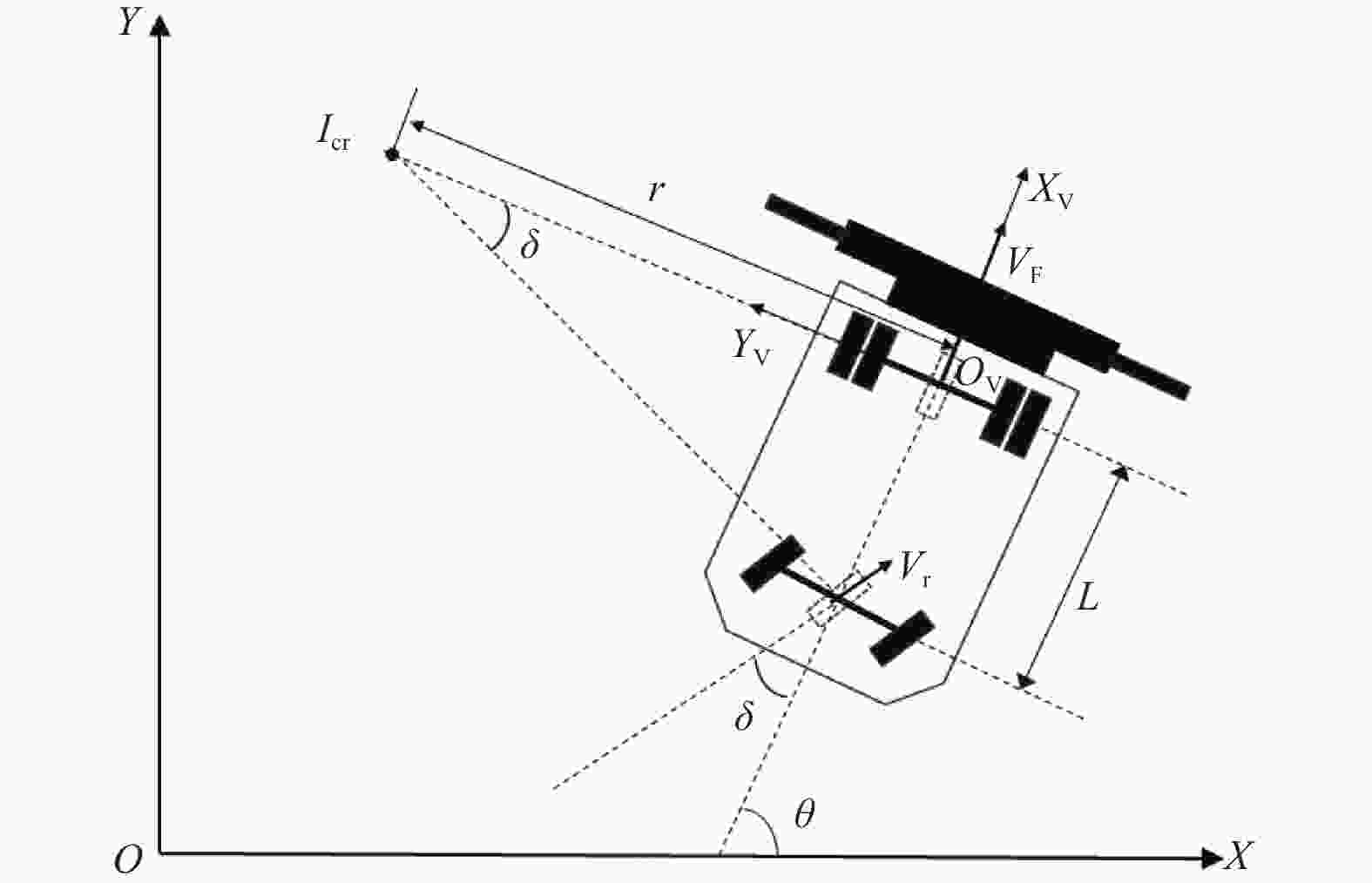
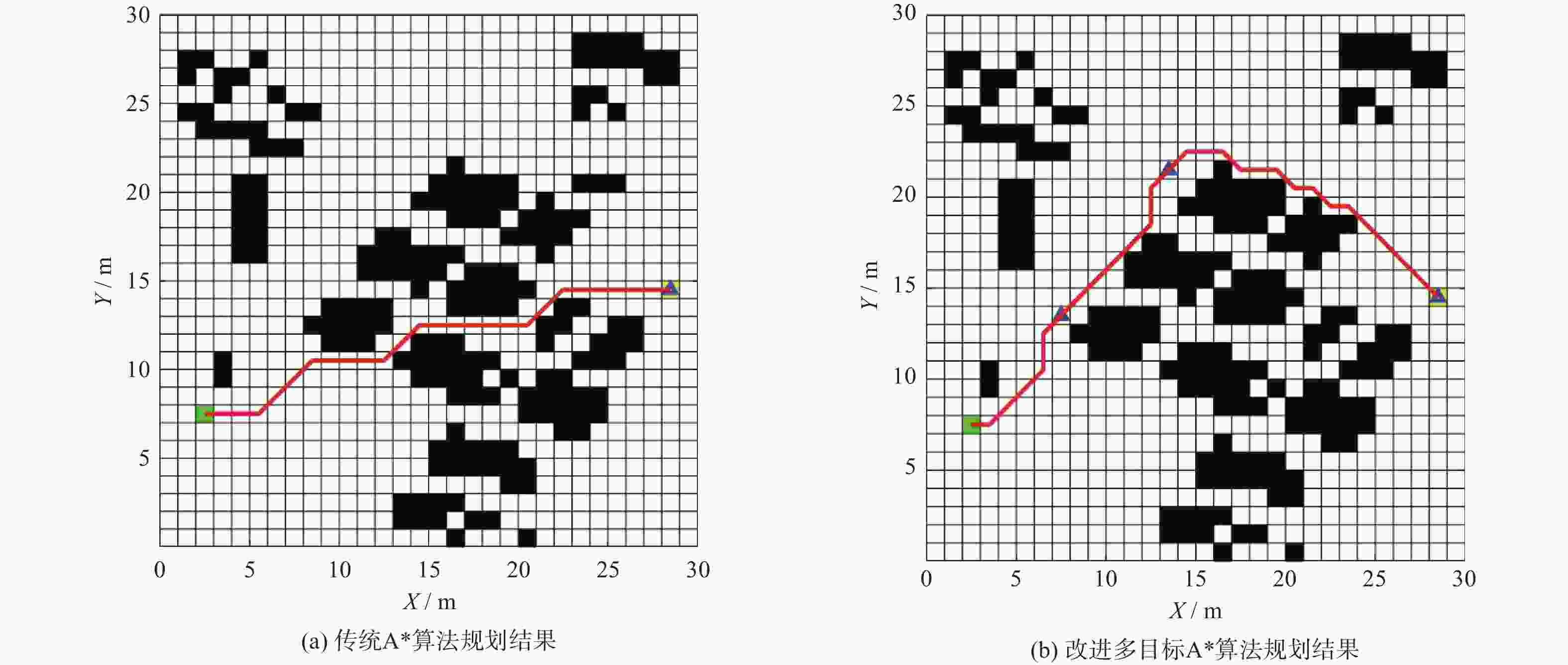
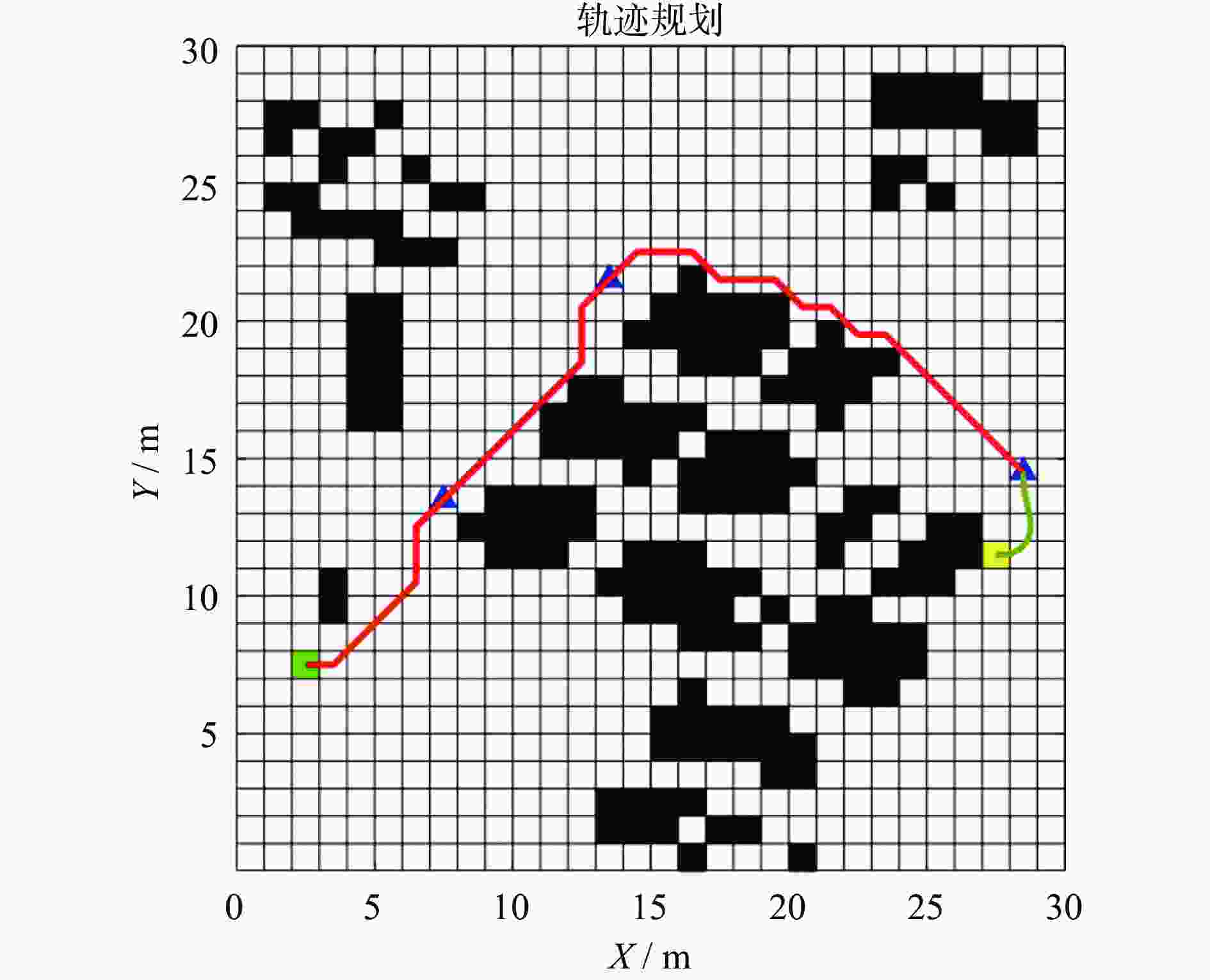
School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

摘要: 集装箱堆场作业环境复杂，实现无人堆高机精准停位是亟须解决的关键问题。对此，设计了基于改进A*算法与多项式螺旋曲线结合的混合策略。首先，基于堆高机作业工况及抓取作业流程，设计多目标点改进A*全局规划算法，通过单次规划依次通过多个给定的目标点；其次，根据非完整约束条件，在靠近最终目标点处设计基于多项式螺旋线的局部规划。选取多种典型作业场景，对提出的算法进行仿真实验及分析。研究结果表明，该策略能使堆高机在全局路径中依次通过多个目标点，并经局部规划调整后满足作业目标点的约束，符合作业要求。
- 空箱堆高机 /
- 多目标点规划 /
- 多约束条件 /
- 改进A*算法 /
- 多项式螺旋线
Abstract: The operational environment of container yards is complex, and achieving precise parking for autonomous empty container handler is a critical problem that need to be solved. To address this, a hybrid strategy combining an improved A* algorithm with polynomial spiral curves was designed. Considering the working conditions and grasping workflow of the empty container handler, a multi-target improved A* global planning algorithm was developed, enabling the sequential traversal of multiple given target points in a single planning process. Furthermore, based on non-holonomic constraints, a local planning strategy utilizing polynomial spiral curves was designed near the final target point. Simulations and analyses were conducted on selected typical operational scenarios to validate the proposed algorithm. The results indicate that the strategy enables the stacker crane to sequentially pass through multiple target points along the global path. After local planning adjustments, it can meet the constraints of the operational target points, thereby fulfilling operational requirements.
- empty container handler /
- multi-target planning /
- multi-constraint conditions /
- improved A* algorithm /
- polynomial spiral curves

HTML全文

图 1 堆高机堆场作业场景

Figure 1. Operation of ECH in container yard

下载: 全尺寸图片幻灯片

图 2 堆场作业对象

Figure 2. Objects of yard operation

下载: 全尺寸图片幻灯片

图 3 堆高机作业流程图

Figure 3. Operation flow chart of ECH

下载: 全尺寸图片幻灯片

图 4 箱区栅格地图

Figure 4. Yard grid map

下载: 全尺寸图片幻灯片

图 5 多目标规划示意图

Figure 5. Multi-objective planning diagram

下载: 全尺寸图片幻灯片

图 6 算法流程图

Figure 6. Algorithm flow diagram

下载: 全尺寸图片幻灯片

图 7 堆高机感知系统示意图

Figure 7. Sensing system of ECH

下载: 全尺寸图片幻灯片

图 8 作业场景示意图

Figure 8. Operation scenario diagram

下载: 全尺寸图片幻灯片

图 9 空箱堆高机运动学模型

Figure 9. Kinematic model of ECH

下载: 全尺寸图片幻灯片

图 10 全局规划结果

Figure 10. Global planning result

下载: 全尺寸图片幻灯片

图 11 场景仿真结果

Figure 11. Scenario simulation results

下载: 全尺寸图片幻灯片

图 12 最终规划结果

Figure 12. Final planning result

下载: 全尺寸图片幻灯片

表 1 空箱堆高机技术参数

Table 1. Technical parameters of ECH 单位：m

车身长度	轮轴距	最小转弯半径	吊具尺寸
6.9	4.5	6	6.11 ~ 12.17

下载: 导出CSV

表 2 不同场景下局部规划算法的参数结果

Table 2. Solution results of local planning parameters in different scenarios

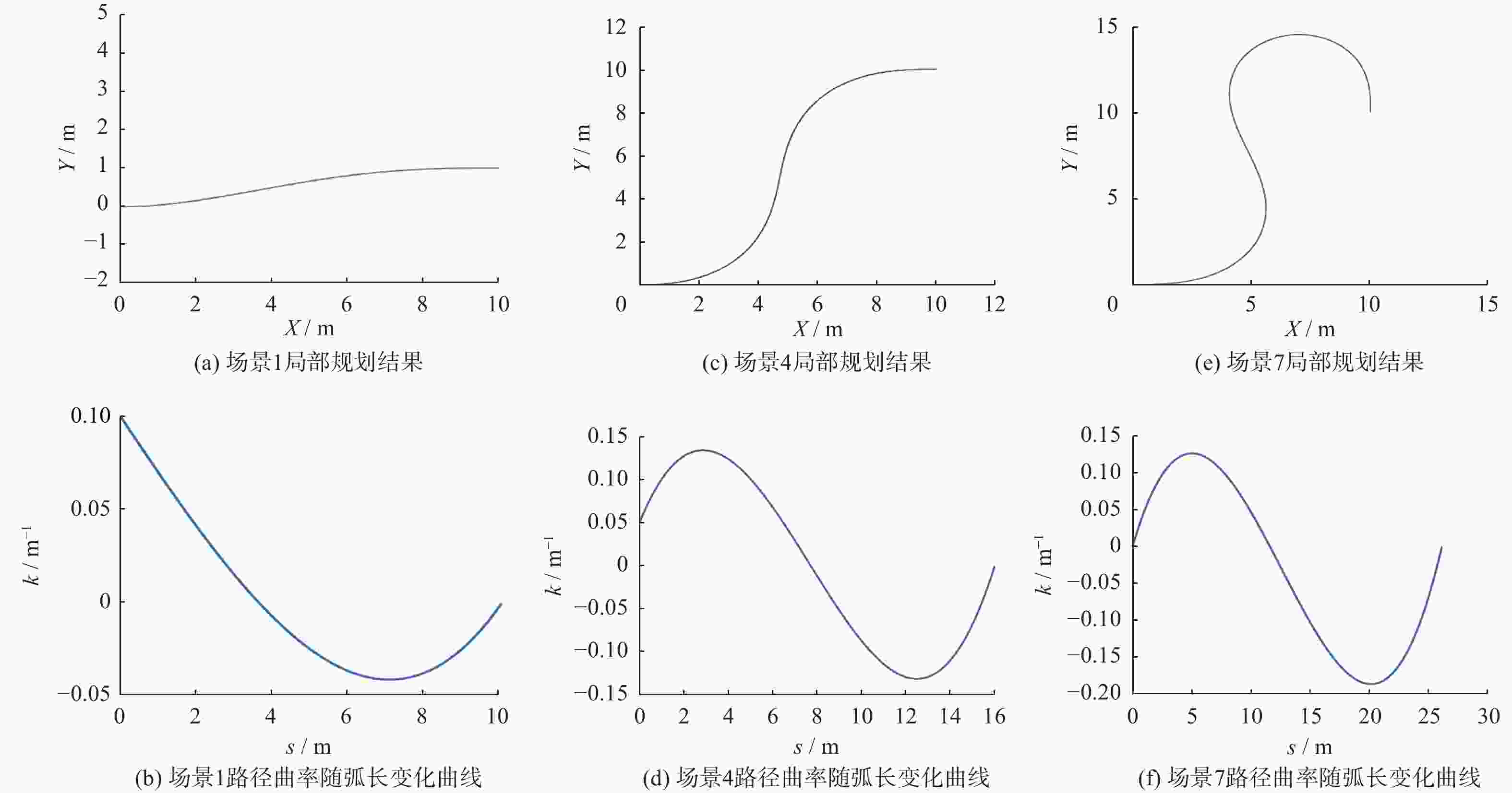
场景	起点曲率/m^-1	目标点坐标	实到点坐标	起始航向角/rad	目标航向角/rad	b	c	s_final
1	0.1	（10, 1）	（10.01, 0.99）	0	0	0.695	−0.402	10.067
2	0.1	(10, 1)	（10.02, 1.00）	0	π/2	−0.550	0.383	12.784
3	0.1	(10, 1)	(10.00, 1.02)	π/2	π/2	−0.380	0.384	16.694
4	0.05	(10, 10)	(10.02, 9.99)	0	0	0.180	−0.213	15.969
5	0.05	(10, 10)	(10.00, 10.02)	0	π/2	0.094	0.133	16.080
6	0.05	(10, 10)	(10.03, 9.99)	π/2	π/2	−0.250	0.214	16.507
7	0	(10, 10)	(10.04, 10.00)	0	−π/2	0.159	−0.319	26.124

下载: 导出CSV

参考文献(18)

[1]	YANG L W, LI P, QIAN S, et al. Path planning technique for mobile robots: a review[J] . Machines, 2023, 11(10): 980. doi: 10.3390/machines11100980
[2]	于向军, 槐元辉, 姚宗伟, 等. 工程车辆无人驾驶关键技术[J] . 吉林大学学报(工学版), 2021, 51(4): 1153−1168.
[3]	鲍庆勇, 李舜酩, 沈峘, 等. 自主移动机器人局部路径规划综述[J] . 传感器与微系统, 2009, 28(9): 1 − 4,11.
[4]	HIRAYAMA M, GUIVANT J, KATUPITIYA J, et al. Path planning for autonomous bulldozers[J] . Mechatronics, 2019, 58: 20 − 38. doi: 10.1016/j.mechatronics.2019.01.001
[5]	WANG X D, ZHANG H W, LIU S, et al. Path planning of scenic spots based on improved A* algorithm[J] . Scientific Reports, 2022, 12: 1320. doi: 10.1038/s41598-022-05386-6
[6]	HARTOMO K, ISMANTO B, NUGRAHA A, et al. Searching the shortest route to distribute disaster’s logistical assistance using Dijkstra method[J] . Journal of Physics: Conference Series, 2019, 1402(7): 077014. doi: 10.1088/1742-6596/1402/7/077014
[7]	AMMAR A, BENNACEUR H, CHÂARI I, et al. Relaxed Dijkstra and A* with linear complexity for robot path planning problems in large-scale grid environments[J] . Soft Computing, 2016, 20(10): 4149 − 4171. doi: 10.1007/s00500-015-1750-1
[8]	刘洋, 章卫国, 李广文. 基于改进PRM算法的路径规划研究[J] . 计算机应用研究, 2012, 29(1): 104 − 106,139.
[9]	符运来, 王魏, 刘妙男, 等. 基于改进P-RRT算法的无人船路径规划[J/OL] . 控制工程*. (2024-04-02)[2024-04-29] . https://doi.org/10.14107/j.cnki.kzgc.20231049.
[10]	PATLE B K, PARHI D R K, JAGADEESH A, et al. Matrix-binary codes based genetic algorithm for path planning of mobile robot[J] . Computers & Electrical Engineering, 2018, 67: 708 − 728.
[11]	黄荣杰, 王亚刚. 基于可视图与改进遗传算法的机器人平滑路径规划[J] . 控制工程, 2024, 31(4): 678 − 686.
[12]	REN J, HUANG X S, HUANG R N. Efficient deep reinforcement learning for optimal path planning[J] . Electronics, 2022, 11(21): 3628. doi: 10.3390/electronics11213628
[13]	罗强, 王海宝, 崔小劲, 等. 改进人工势场法自主移动机器人路径规划[J] . 控制工程, 2019, 26(6): 1091 − 1098.
[14]	王洪斌, 尹鹏衡, 郑维, 等. 基于改进的A^*算法与动态窗口法的移动机器人路径规划[J] . 机器人, 2020, 42(3): 346 − 353.
[15]	GIM S, ADOUANE L, LEE S, et al. Clothoids composition method for smooth path generation of car-like vehicle navigation[J] . Journal of Intelligent & Robotic Systems, 2017, 88(1): 129 − 146.
[16]	吕恩利, 林伟加, 刘妍华, 等. 基于B样条曲线的智能叉车托盘拾取路径规划研究[J] . 农业机械学报, 2019, 50(5): 394 − 402.
[17]	HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J] . IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100 − 107.
[18]	龚纯, 王正林. 精通MATLAB最优化计算[M] . 3版. 北京: 电子工业出版社, 2014.