压电驱动纳米定位平台迟滞补偿与速度位置正反馈谐振控制

司马津甫; 赖磊捷

doi:10.12299/jsues.24-0201

压电驱动纳米定位平台迟滞补偿与速度位置正反馈谐振控制

doi: 10.12299/jsues.24-0201

司马津甫,
赖磊捷^,

上海工程技术大学机械与汽车工程学院, 上海 201620

基金项目: 上海市自然科学基金（21ZR1426000）

详细信息

作者简介:
司马津甫（1999 − ），男，硕士生，研究方向为微纳米定位技术。 E-mail：smajinfu@163.com

通讯作者:
赖磊捷（1984 − ），男，副教授，博士，研究方向为微位移驱动控制、微纳制造装备等。E-mail：lailj@sues.edu.cn

中图分类号: TN384
计量
- 文章访问数: 15
- HTML全文浏览量: 7
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2024-07-12
- 网络出版日期: 2026-02-02
- 刊出日期: 2025-12-01

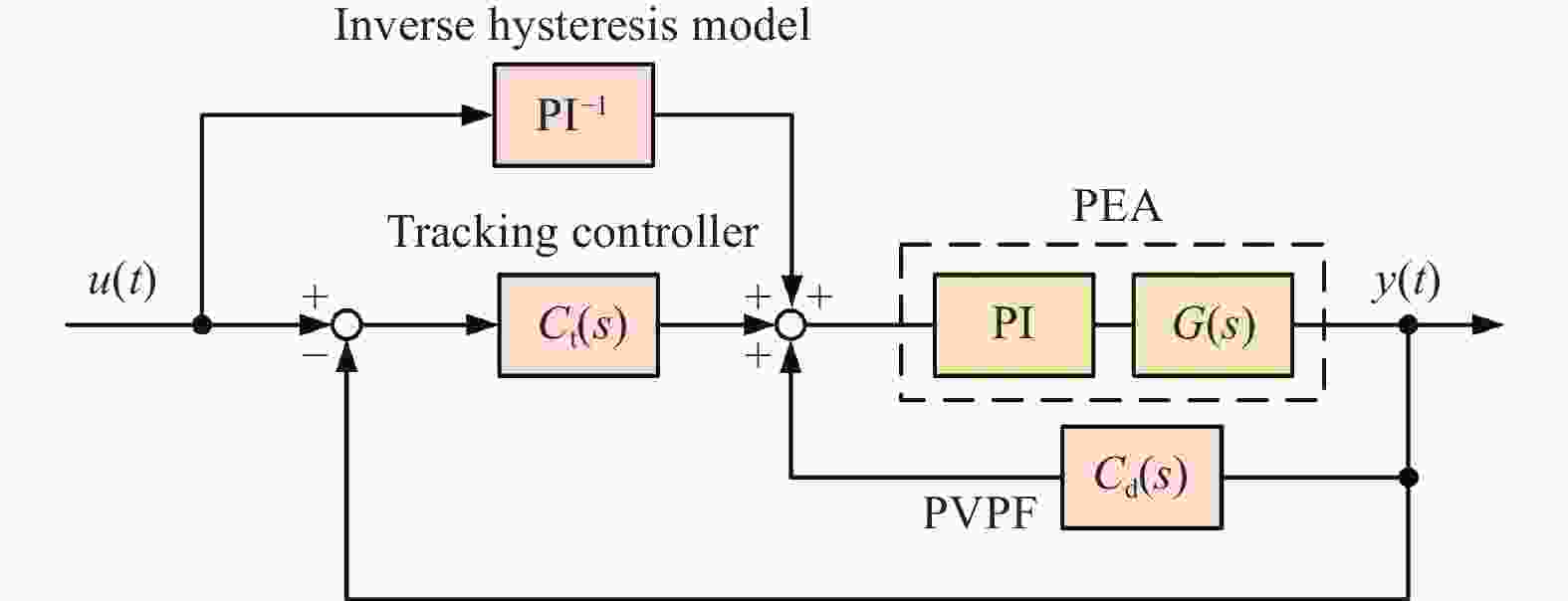
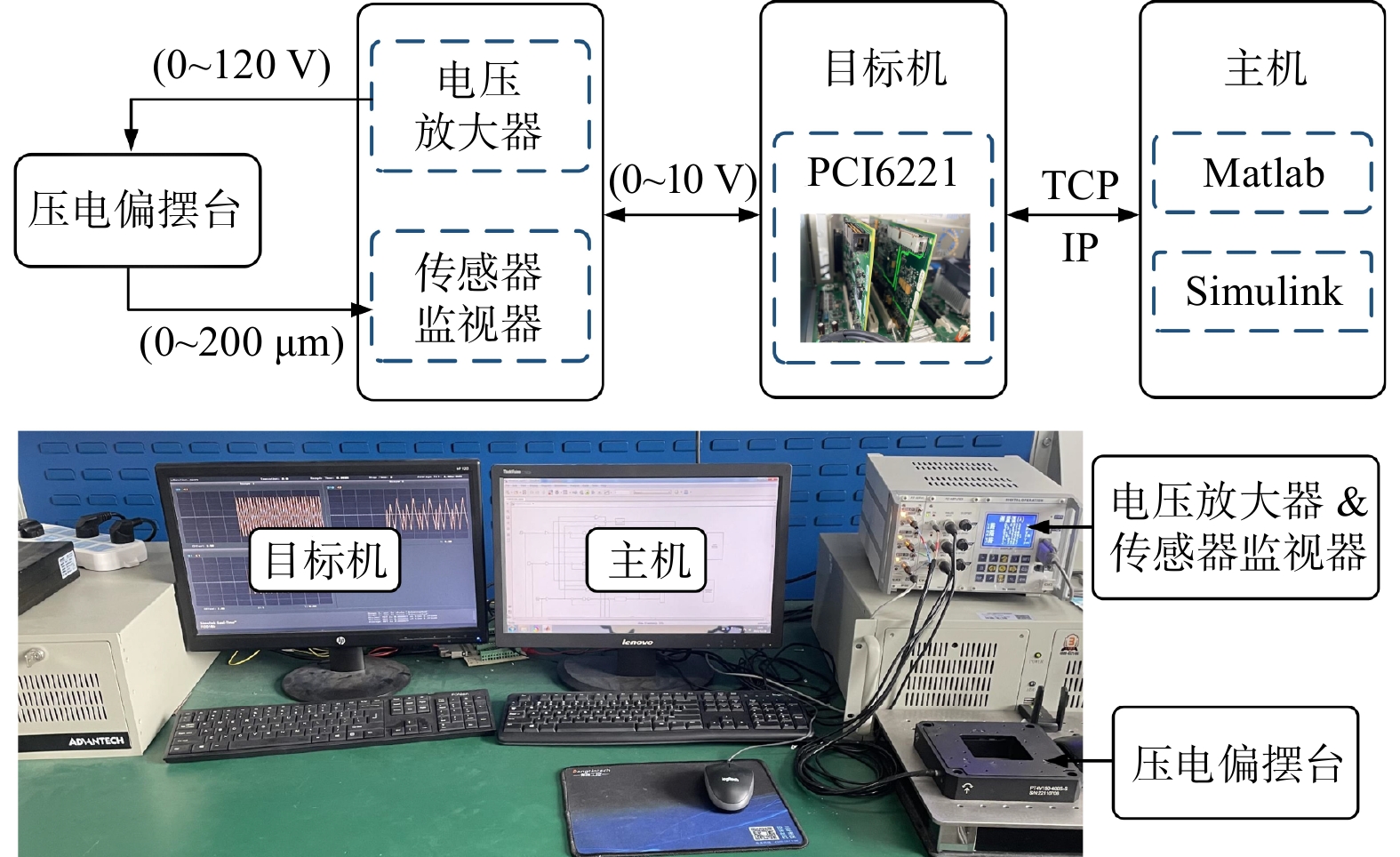
Hysteresis compensation and positive velocity-position feedback resonance control of piezoelectric driven nanopositioning stage

SIMA Jinfu,
LAI Leijie^,

School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

摘要

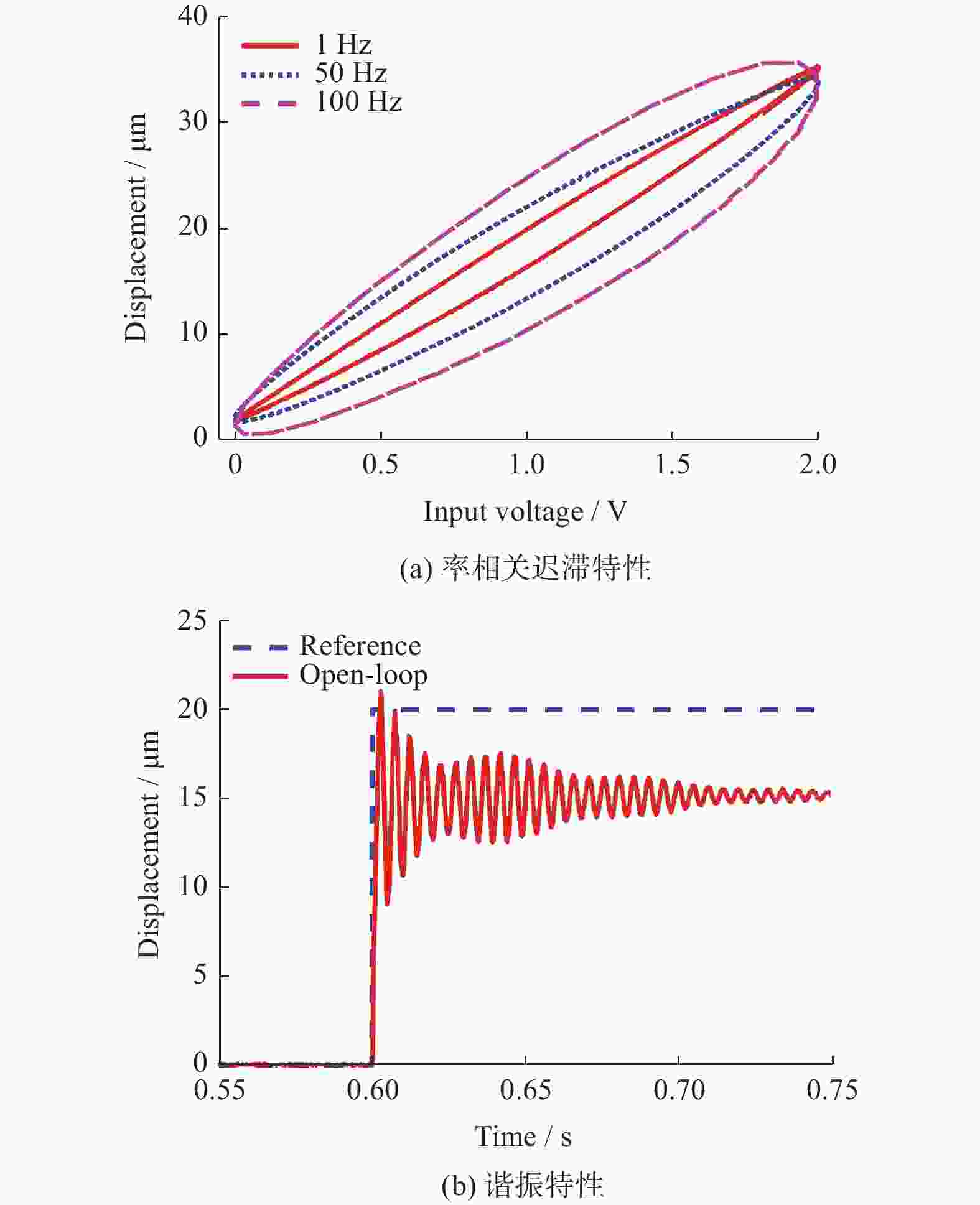
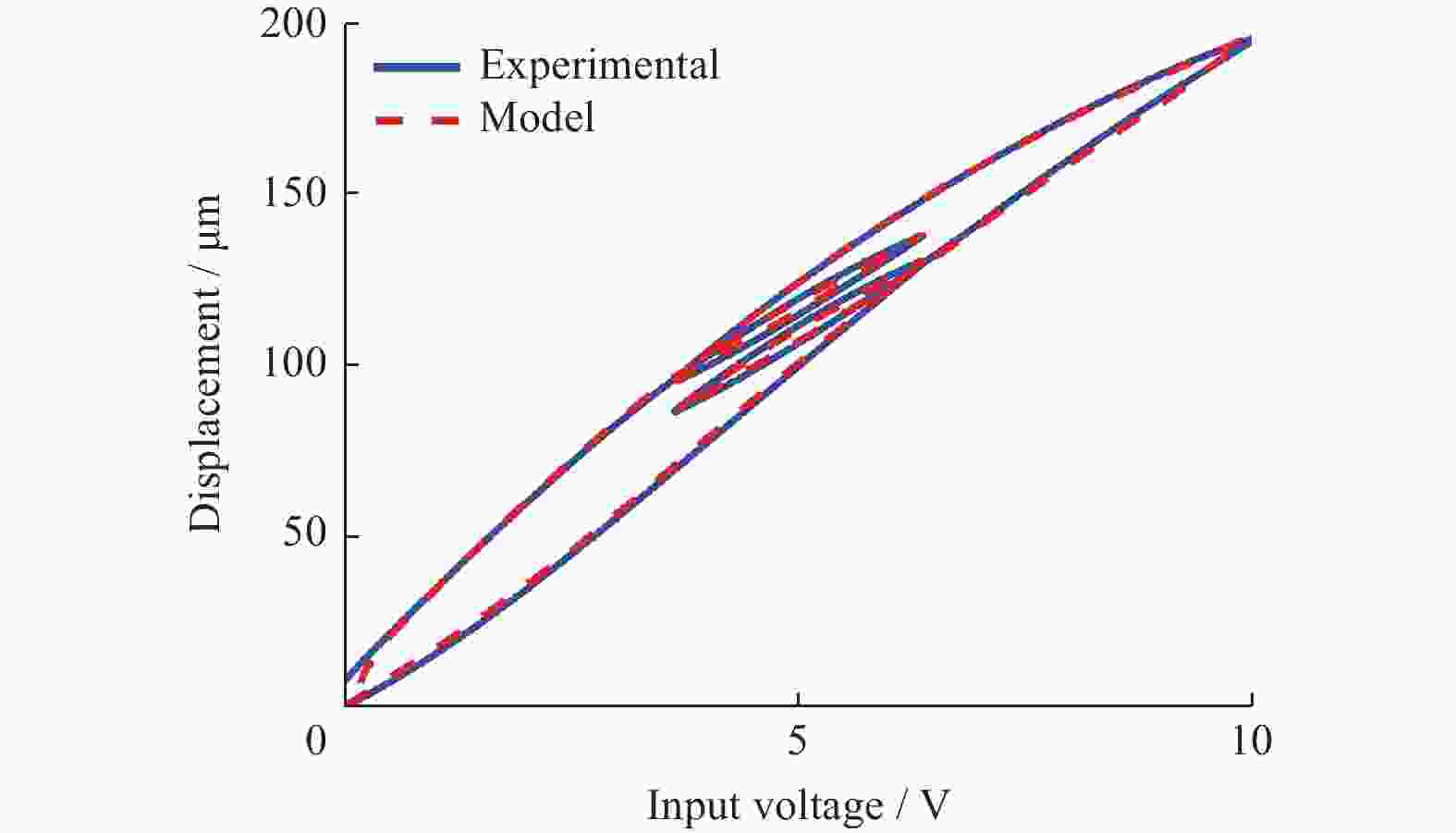
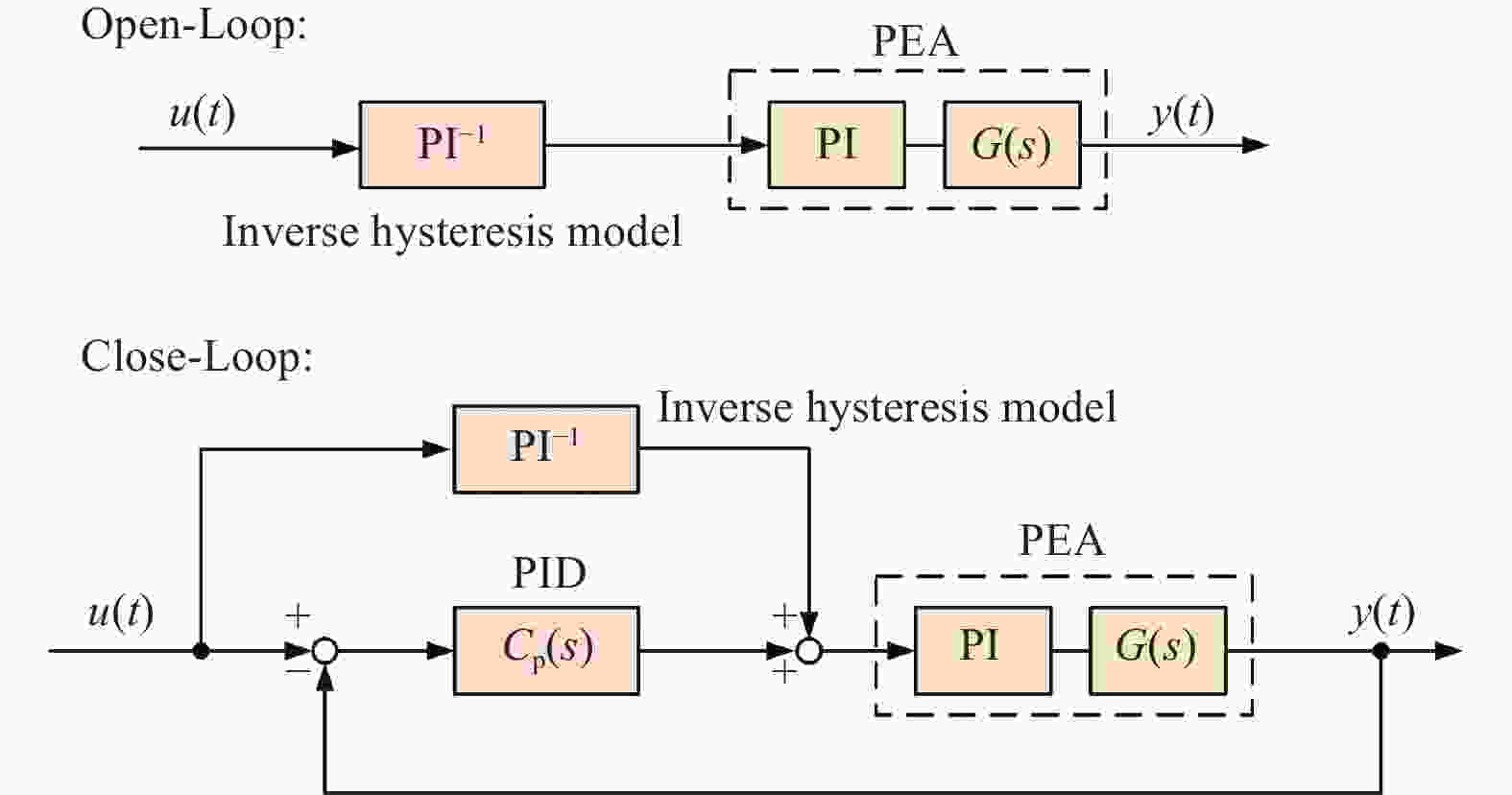
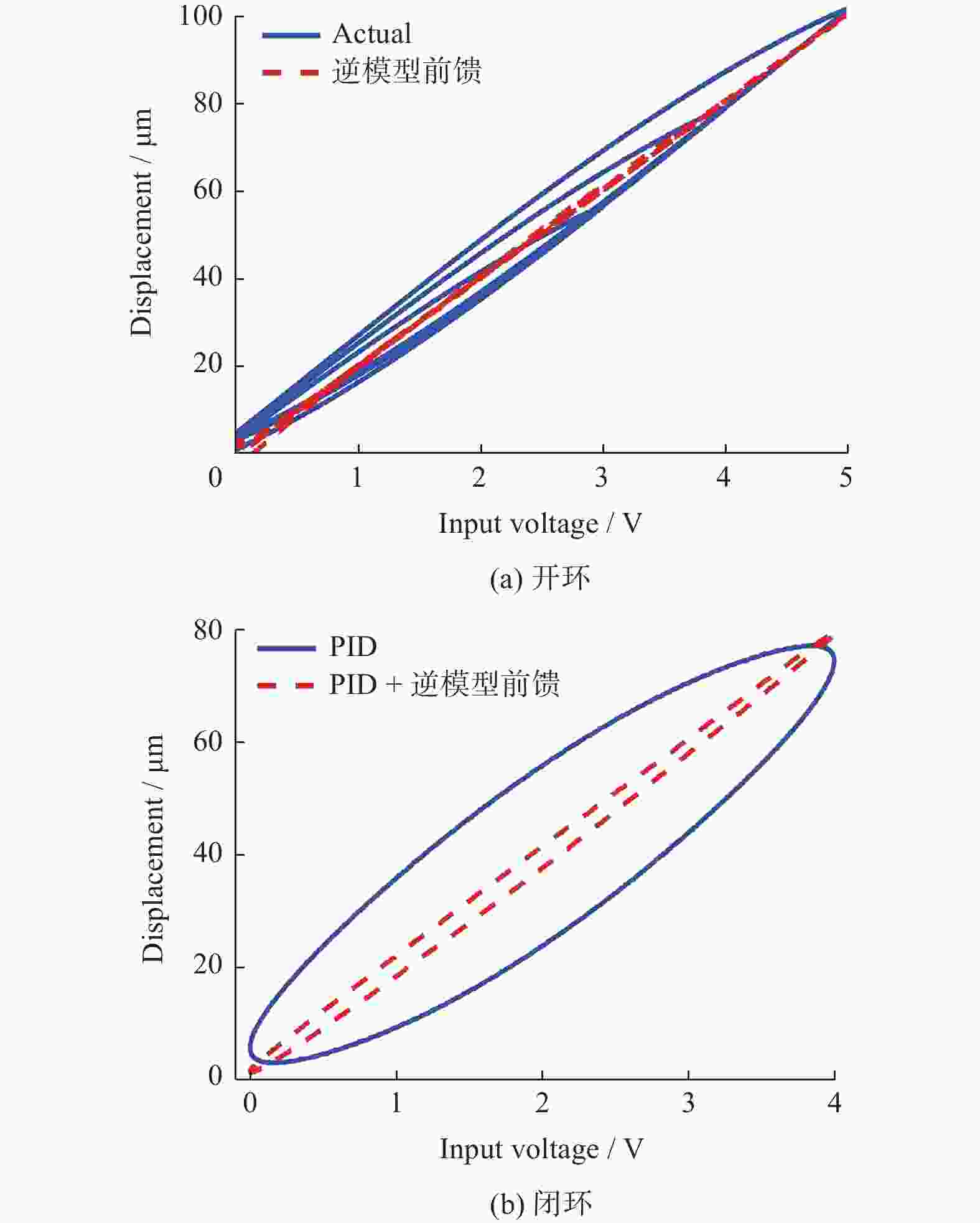
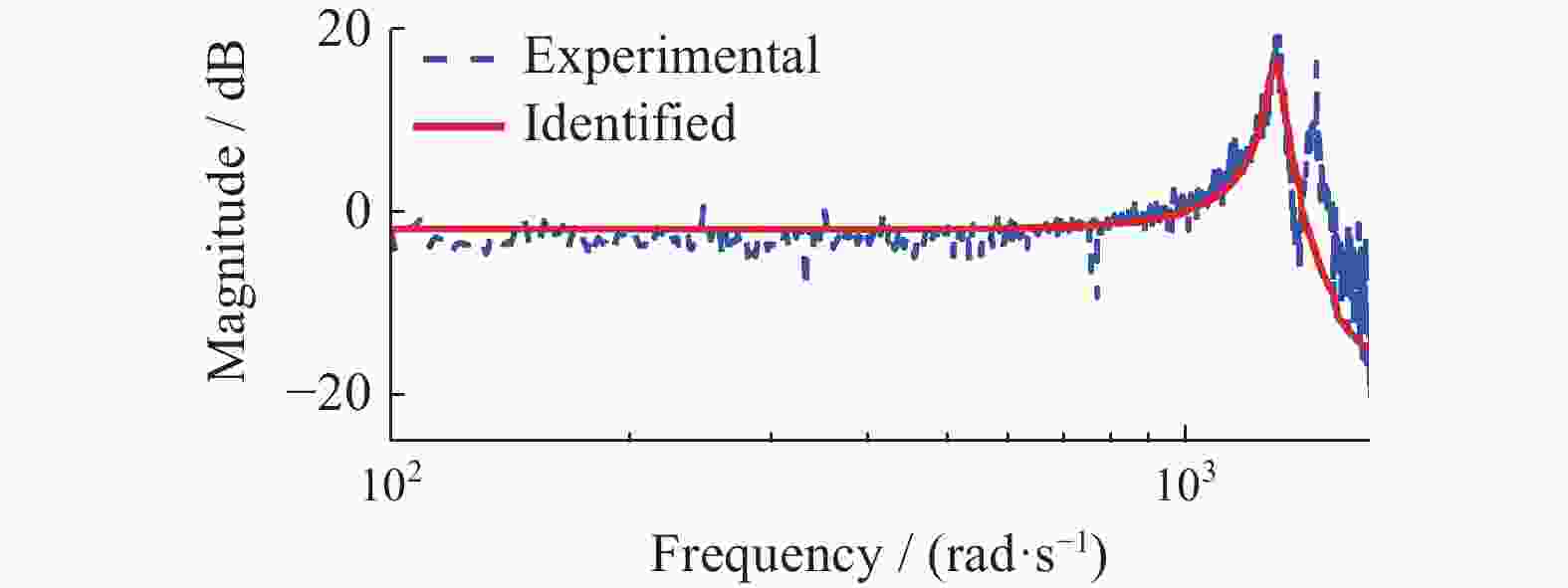
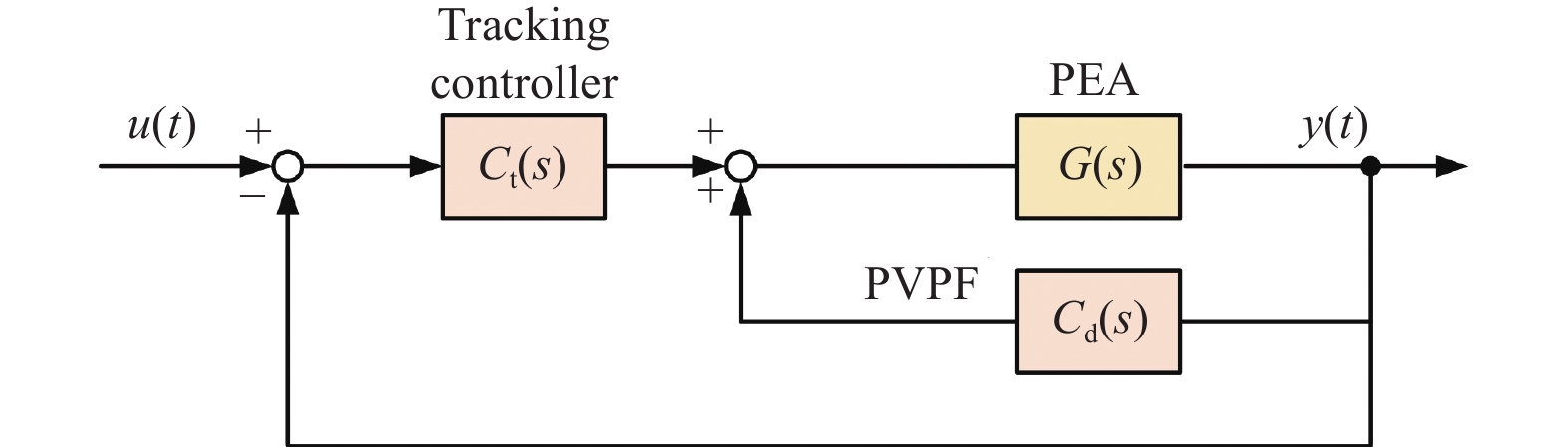
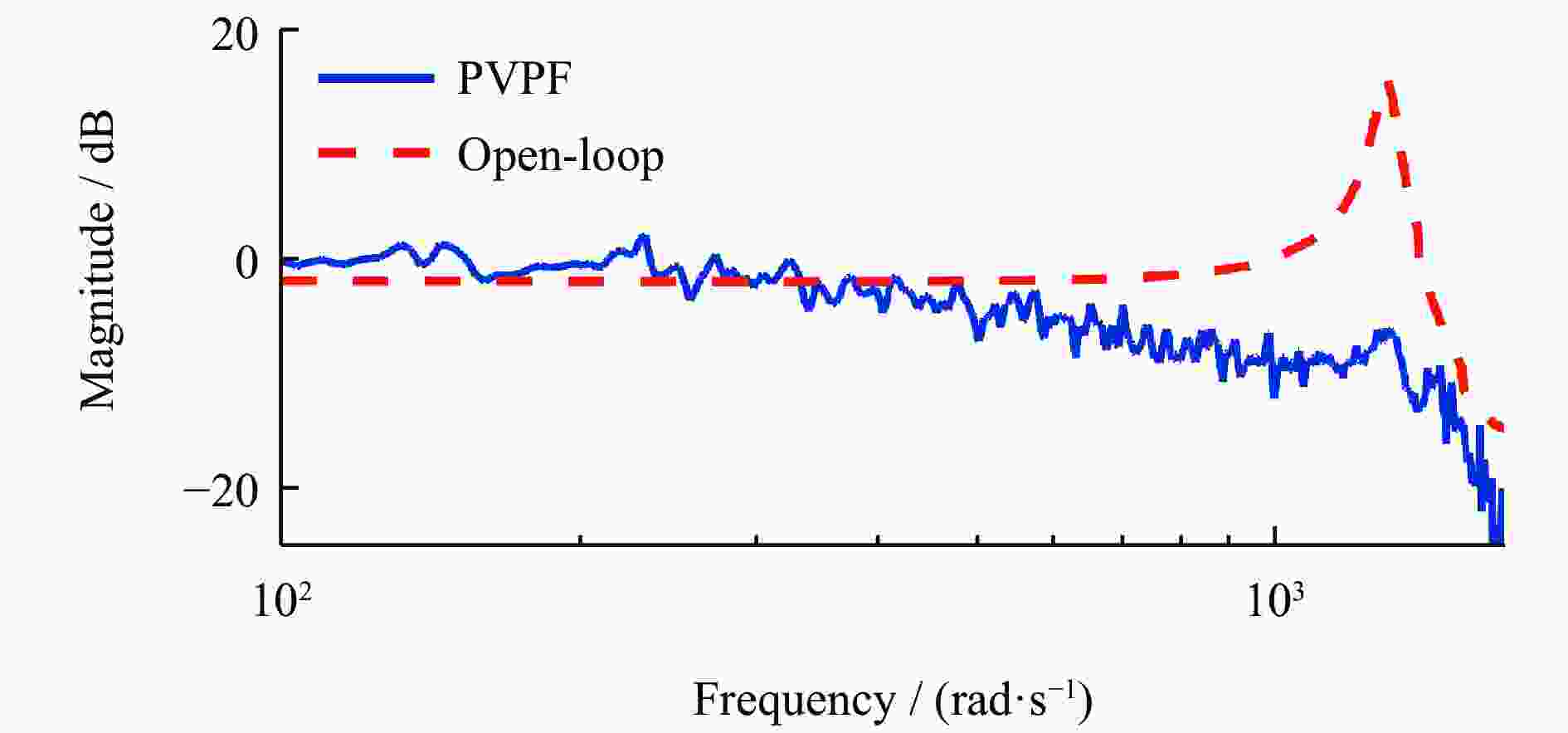
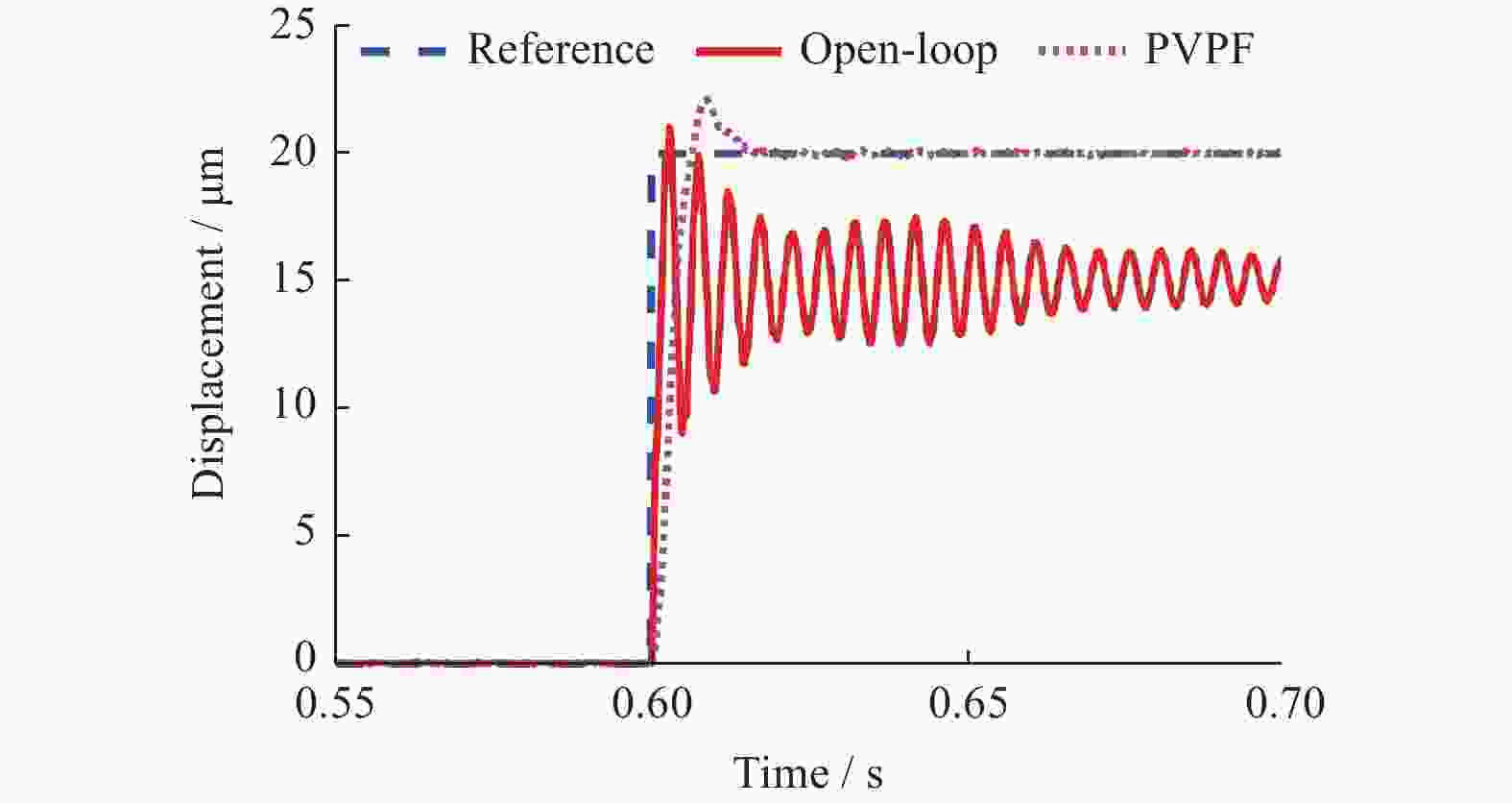
摘要: 为解决压电驱动纳米定位平台的迟滞问题与低阻尼谐振问题，构建了三自由度压电驱动纳米定位平台实验系统，分析定位平台的迟滞和谐振特性。建立率相关Prandtl-Ishlinskii迟滞模型，对逆模型进行参数辨识，通过开环和闭环前馈补偿实验验证了模型的有效性和准确性。采用基于巴特沃斯滤波器形式的极点配置方法，设计了积分跟踪控制器和速度−位置正反馈阻尼控制器的参数，并验证了阻尼控制器的有效性。通过复合控制方法进行轨迹跟踪实验，实验结果表明，该方法显著提升了压电定位台的跟踪精度与速度，证明所提控制方法的有效性。
- 压电驱动器 /
- 纳米定位平台 /
- 迟滞模型 /
- 逆补偿 /
- 阻尼控制
Abstract: To address the hysteresis and low damping resonance problems of piezoelectric driven nanopositioning stages, a three-degree-of-freedom piezoelectric driven nanopositioning stage experimental system was constructed, and the hysteresis and resonance characteristics were analyzed. A rate-dependent Prandtl-Ishlinskii hysteresis model was established, and the parameters of its inverse model were identified. The effectiveness and accuracy of the model were verified through open-loop and close-loop feedforward compensation experiments. Subsequently, a pole placement method based on a Butterworth filter was employed to design the parameters of an integral tracking controller and a positive velocity-position feedback (PVPF) damping controller, and the effectiveness of the damping controller was verified. Finally, trajectory tracking experiments were conducted using a composite control method. The experimental results show that this method significantly improves the tracking accuracy and speed of the piezoelectric positioning stage, demonstrating the effectiveness of the proposed control method.
- piezoelectric actuators /
- nanopositioning stage /
- hysteresis model /
- inverse compensation /
- damping control

HTML全文

图 1 实验系统

Figure 1. Experimental system

下载: 全尺寸图片幻灯片

图 2 率相关迟滞及谐振特性

Figure 2. Rate-dependent hysteresis and resonance characteristics

下载: 全尺寸图片幻灯片

图 3 PI逆模型参数辨识结果

Figure 3. Identification results of inverse PI model parameters

下载: 全尺寸图片幻灯片

图 4 系统控制框图

Figure 4. System control block diagram

下载: 全尺寸图片幻灯片

图 5 开环与闭环轨迹跟踪结果

Figure 5. Open-loop and closed-loop trajectory tracking results

下载: 全尺寸图片幻灯片

图 6 平台辨识结果与实际频响对比

Figure 6. Comparison of frequency response between stage identification results and actual results

下载: 全尺寸图片幻灯片

图 7 PVPF控制框图

Figure 7. PVPF control block diagram

下载: 全尺寸图片幻灯片

图 8 平台频响特性对比

Figure 8. Comparison of stage frequency response characteristics

下载: 全尺寸图片幻灯片

图 9 阶跃信号跟踪实验

Figure 9. Step signal tracking experiment

下载: 全尺寸图片幻灯片

图 10 复合控制框图

Figure 10. Composite control block diagram

下载: 全尺寸图片幻灯片

图 11 余弦信号轨迹跟踪结果

Figure 11. Cosine signal trajectory tracking results

下载: 全尺寸图片幻灯片

表 1 迟滞逆模型辨识参数

Table 1. Identification parameters of inverse hysteresis model

变量	数值	变量	数值
a₁	0.002 0	b₄	−0.058 6
a₂	1.291 0	b₅	−0.009 7
a₃	0.006 8	b₆	−0.023 9
a₄	0.007 3	b₇	−0.020 9
b₁	−0.136 5	b₈	0
b₂	−0.150 1	b₉	−0.005 3
b₃	−0.129 8	b₁₀	−0.209 8

下载: 导出CSV

表 2 余弦信号跟踪误差

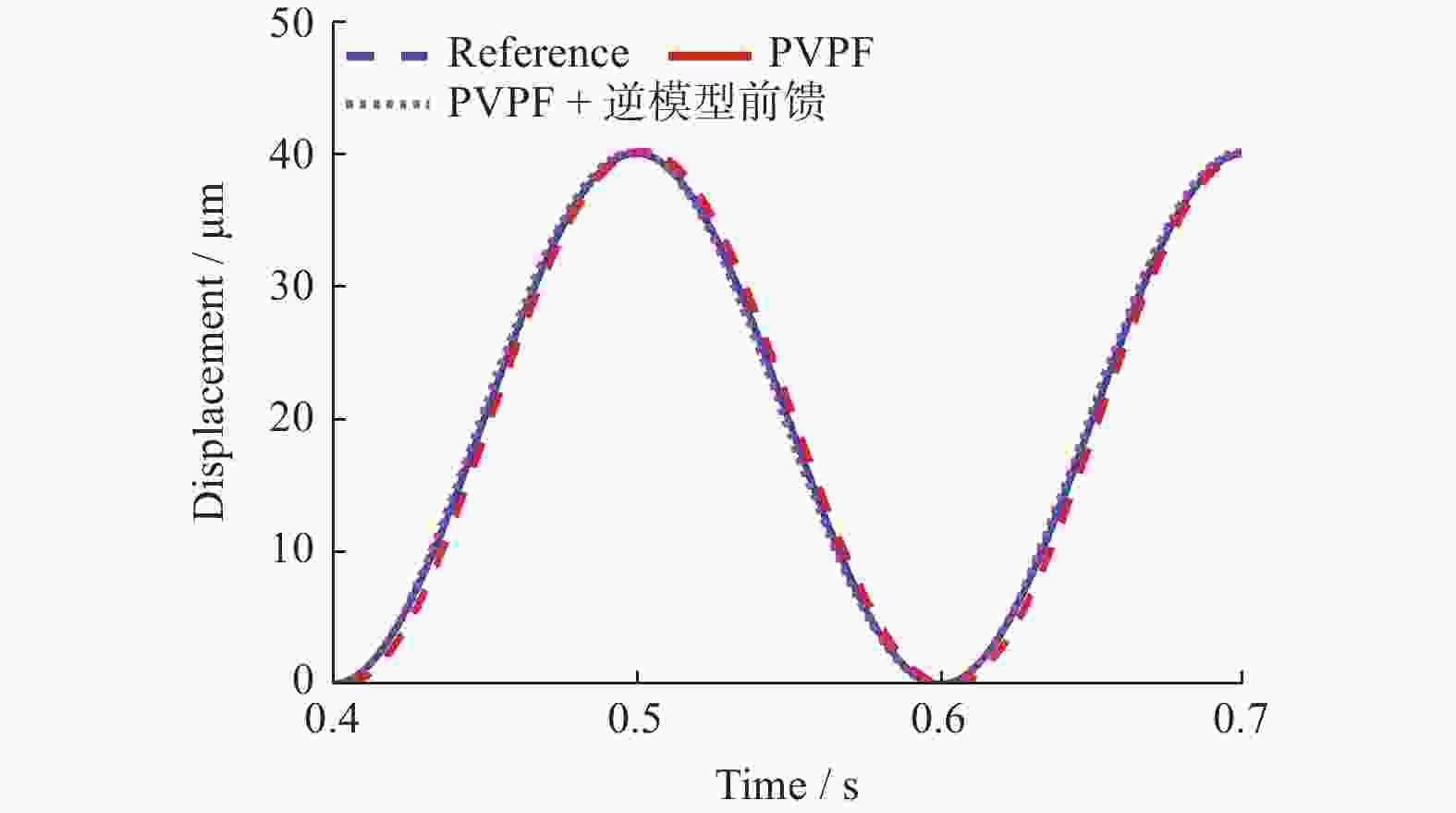
Table 2. Cosine signal tracking error 单位：μm

模型	最大误差	均方根误差
PVPF	1.446 6	0.978 7
PVPF + 逆模型前馈	0.931 6	0.486 8

下载: 导出CSV

参考文献(13)

[1]	范伟, 余晓芬, 奚琳. 压电陶瓷驱动系统及控制方法研究[J] . 光学精密工程, 2007, 15(3): 368 − 371.
[2]	LI L L, LI C X, GU G Y, et al. Positive acceleration, velocity and position feedback based damping control approach for piezo-actuated nanopositioning stages[J] . Mechatronics, 2017, 47: 97 − 104. doi: 10.1016/j.mechatronics.2017.09.003
[3]	LING J, FENG Z, MING M, et al. Damping controller design for nanopositioners: a hybrid reference model matching and virtual reference feedback tuning approach[J] . International Journal of Precision Engineering and Manufacturing, 2018, 19(1): 13 − 22. doi: 10.1007/s12541-018-0002-6
[4]	DAI Y L, LI D Q, WANG D. Review on the nonlinear modeling of hysteresis in piezoelectric ceramic actuators[J] . Actuators, 2023, 12(12): 442. doi: 10.3390/act12120442
[5]	GAN J Q, MEI Z, CHEN X L, et al. A modified Duhem model for rate-dependent hysteresis behaviors[J] . Micromachines, 2019, 10(10): 680. doi: 10.3390/mi10100680
[6]	顾胜良, 王建平, 胡红专, 等. 基于Preisach模型的光纤定位单元R机构精定位的实现[J] . 光学精密工程, 2022, 30(18): 2205 − 2218.
[7]	SU X H, LIU Z, ZHANG Y, et al. Event-triggered adaptive fuzzy tracking control for uncertain nonlinear systems preceded by unknown Prandtl–Ishlinskii hysteresis[J] . IEEE Transactions on Cybernetics, 2021, 51(6): 2979 − 2992. doi: 10.1109/TCYB.2019.2949022
[8]	王贞艳, 贾高欣. 压电陶瓷作动器非对称迟滞建模与内模控制[J] . 光学精密工程, 2018, 26(10): 2484 − 2492.
[9]	张东岳, 王伟国, 张振东, 等. 压电偏摆台的复合控制[J] . 压电与声光, 2017, 39(1): 40 − 43.
[10]	APHALE S S, FLEMING A J, MOHEIMANI S O R. Integral resonant control of collocated smart structures[J] . Smart Materials and Structures, 2007, 16(2): 439 − 446. doi: 10.1088/0964-1726/16/2/023
[11]	LING J, FENG Z, KANG X, et al. Bandwidth enhancement in damping control for piezoelectric nanopositioning stages with load uncertainty: design and implementation[J] . Journal of Vibration and Control, 2021, 27(11/12): 1382 − 1394.
[12]	SAN-MILLAN A, RUSSELL D, FELIU V, et al. A modified positive velocity and position feedback scheme with delay compensation for improved nanopositioning performance[J] . Smart Materials and Structures, 2015, 24(7): 075021. doi: 10.1088/0964-1726/24/7/075021
[13]	EIELSEN A A, VAGIA M, GRAVDAHL J T, et al. Damping and tracking control schemes for nanopositioning[J] . IEEE/ASME Transactions on Mechatronics, 2014, 19(2): 432 − 444. doi: 10.1109/TMECH.2013.2242482