Path following control of unmanned vehicle based on improved model predictive control
-
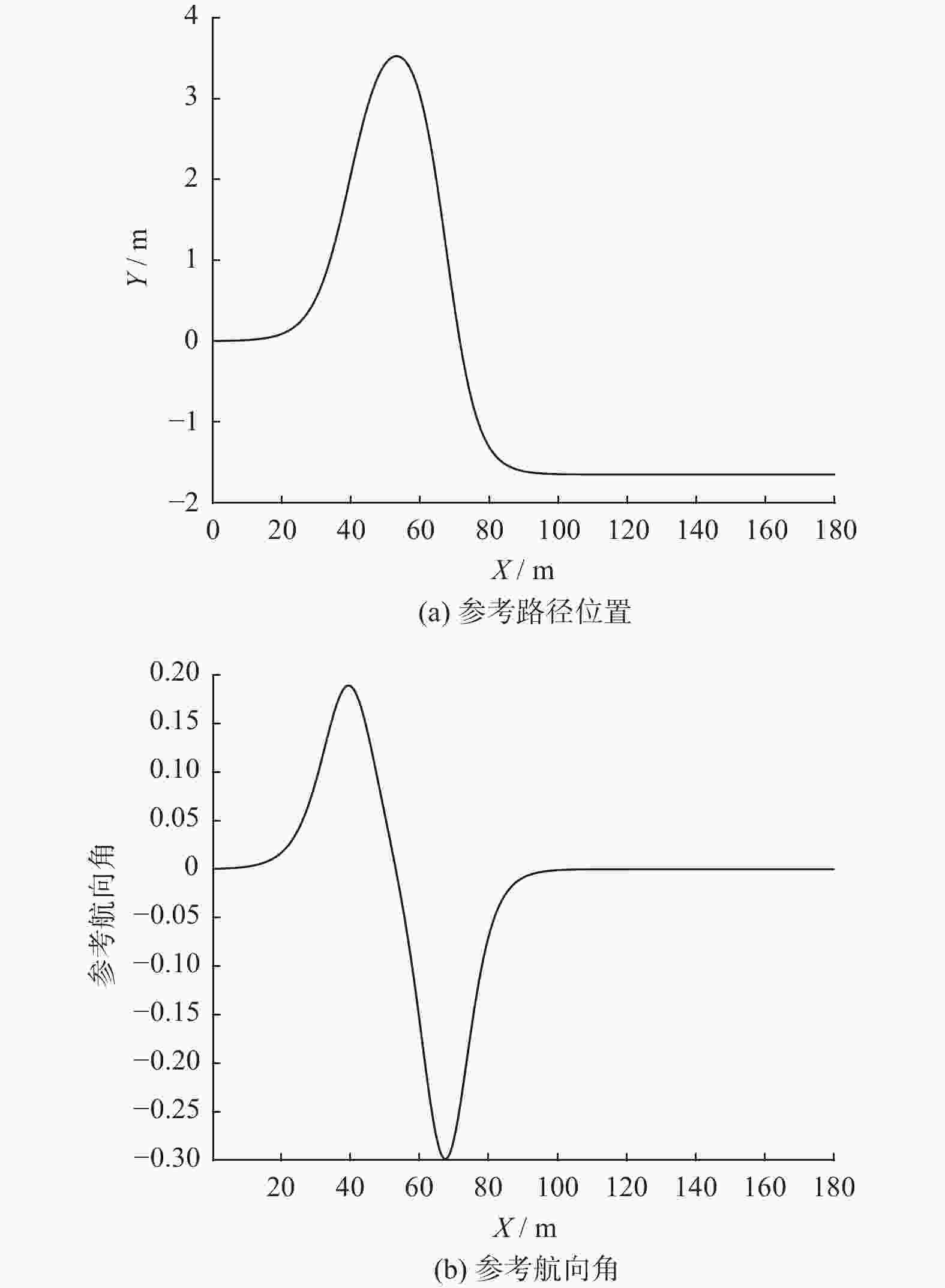
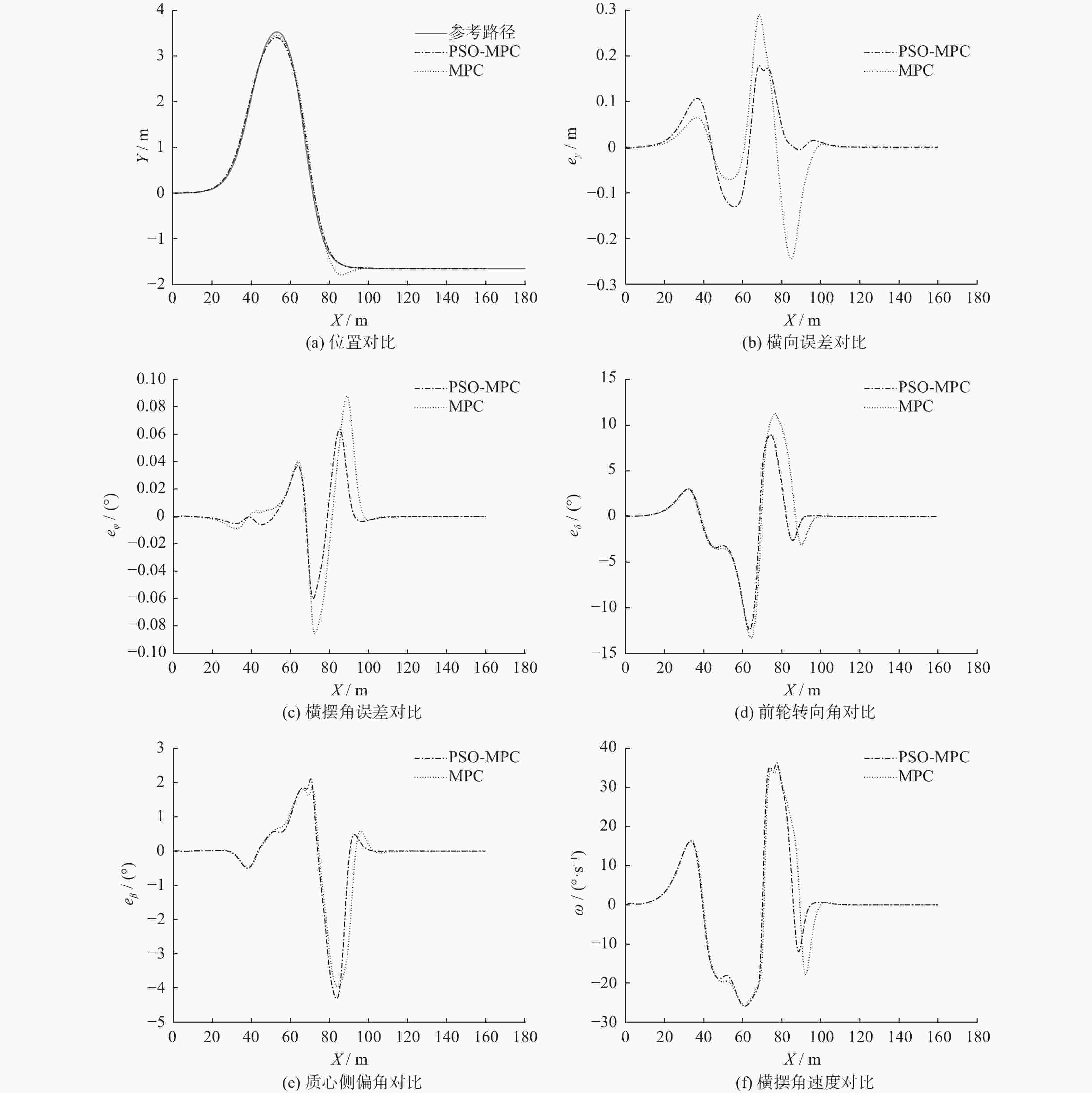
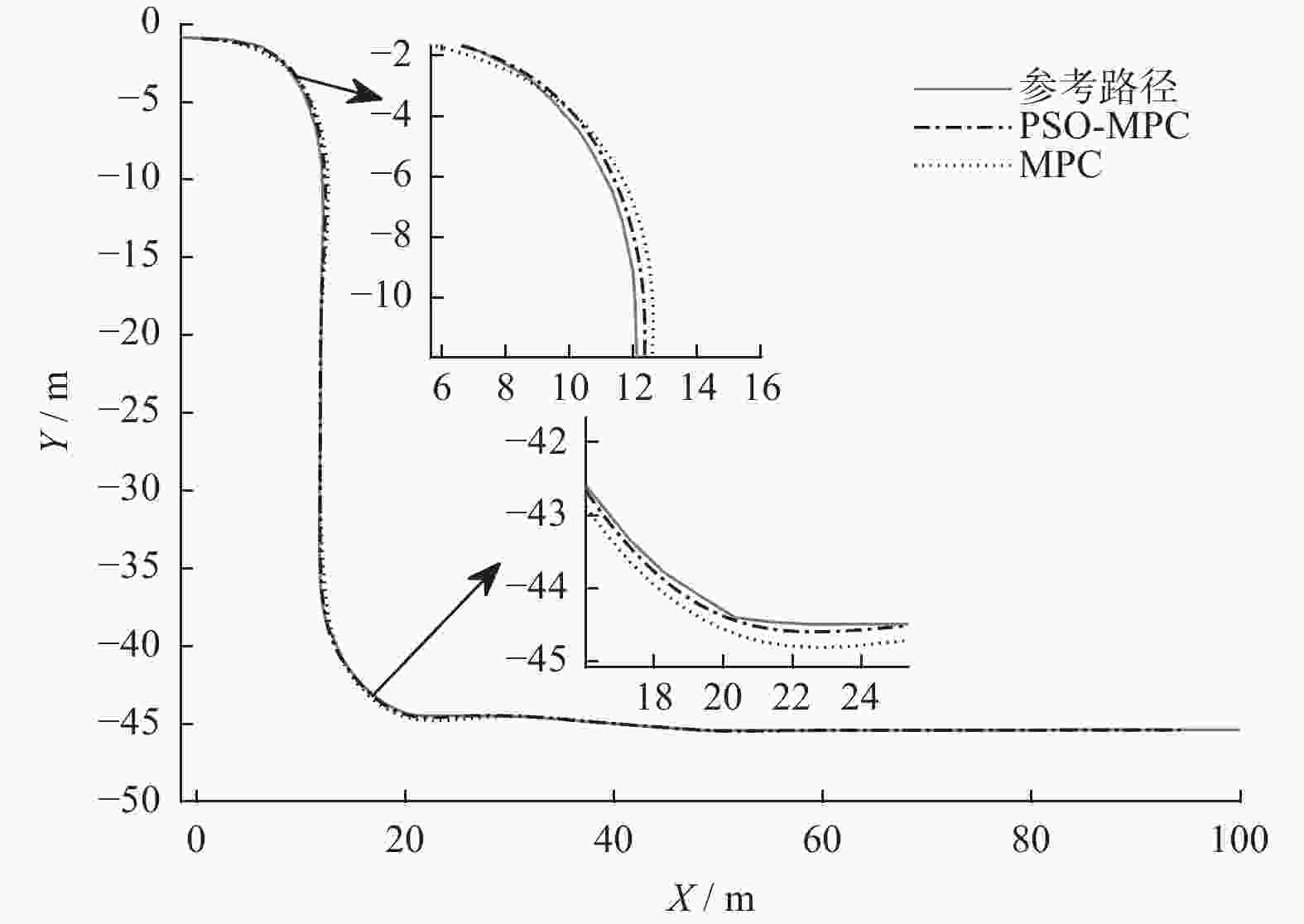
摘要: 为提高无人驾驶车辆路径跟踪精度和稳定性，提出一种基于粒子群优化(Particle Swarm Optimization, PSO)和高斯过程回归(Gaussian Process Regression, GPR)的模型预测控制（Model Predictive Control，MPC）参数自适应方法(PSO-MPC). 使用PSO离线优化MPC参数，利用GPR生成最优参数曲面，可在各种工况下提高无人驾驶车辆路径跟踪的性能. 仿真结果表明，改进的MPC方法在整个路径跟踪过程中能保持车辆稳定性，同时实现良好的路径跟踪精度. 最后，在真实的无人驾驶车辆上验证了改进的MPC方法的有效性.Abstract: In order to improve the path following accuracy and stability of unmanned vehicles, a parameter adaptive model predictive control (MPC) method based on particle swarm optimization (PSO) and Gaussian process regression (GPR) was proposed. By using PSO to optimize MPC parameters offline and GPR to generate optimal parametric surfaces, the path following performances of unmanned vehicles can be improved under various working conditions. The simulated results show that the improved MPC method achieves good path tracking accuracy while maintaining vehicle stability throughout the path following process. Finally, the effectiveness of the improved MPC method was verified on a real unmanned vehicle.
-
图 1 考虑路径曲率的车辆横向动力学模型
Figure 1. Vehicle lateral dynamics model considering path curvature
图 3 PSO优化
${N_{\rm{p}}}$ 和${N_{\rm{c}}}$ 的适应度值Figure 3. Fitness value of PSO at
${N_{\rm{p}}}$ and${N_{\rm{c}}}$ 表 1 MPC控制器参数
Table 1. MPC controller parameters
参数 数值 采样周期$T$/${\rm{s}}$ 0.05 前轮转向角控制量$u$/(°) −35 ~ 35 前轮转向角控制增量$\Delta u$ −0.47 ~ 0.47 
下载: 导出CSV
表 2 车辆参数
Table 2. Vehicle parameters
参数 数值 汽车质量$m$/${\rm{kg}}$ 1412 质心到前轴距离${l_{\rm{f}}}$/${\rm{m}}$ 1.015 质心到后轴距离${l_{\rm{r}}}$/${\rm{m}}$ 1.895 转动惯量${I_{z } }$/(${\rm{kg}} \cdot {{\rm{m}}^2}$) 1537 前轮侧偏刚度${C_{\rm{f}}}$/(${\rm{N}} \cdot {\rm{ra}}{{\rm{d}}^{ - 1}}$) 149000 后轮侧偏刚度${C_{\rm{r}}}$/(${\rm{N}} \cdot {\rm{ra}}{{\rm{d}}^{ - 1}}$) 82200
下载: 导出CSV
表 3 20 m/s控制器参数
Table 3. Controller parameters at 20 m/s
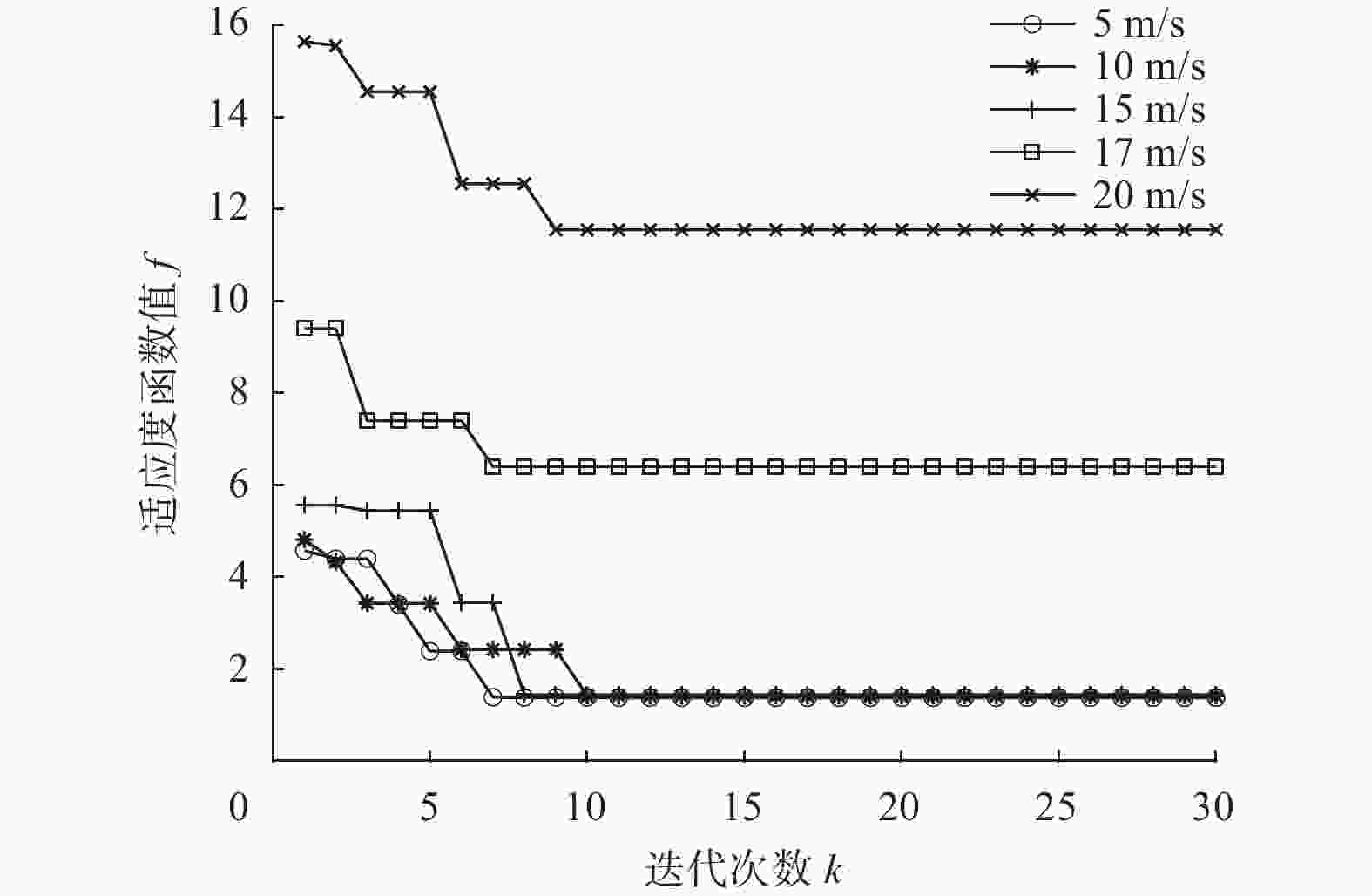
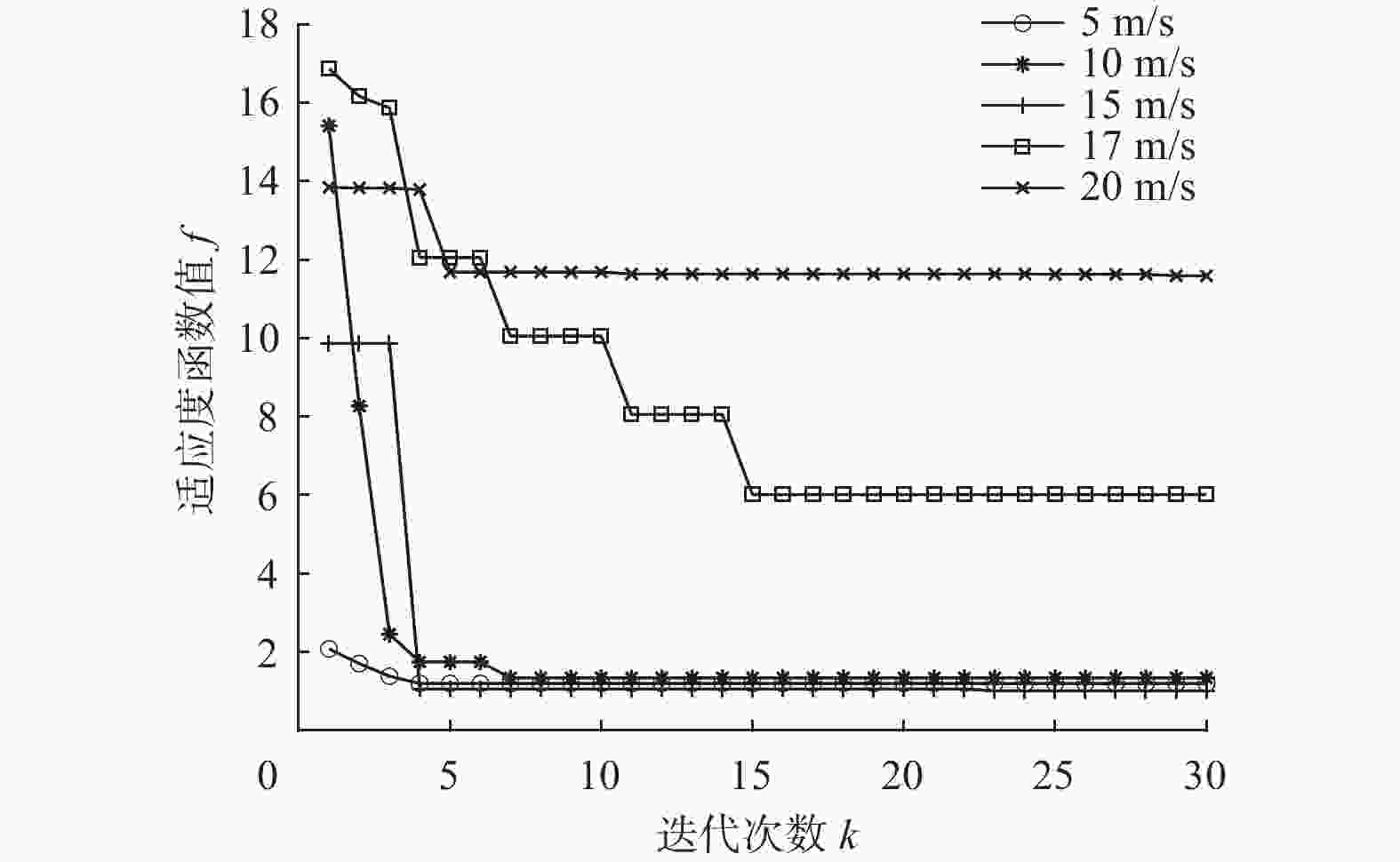
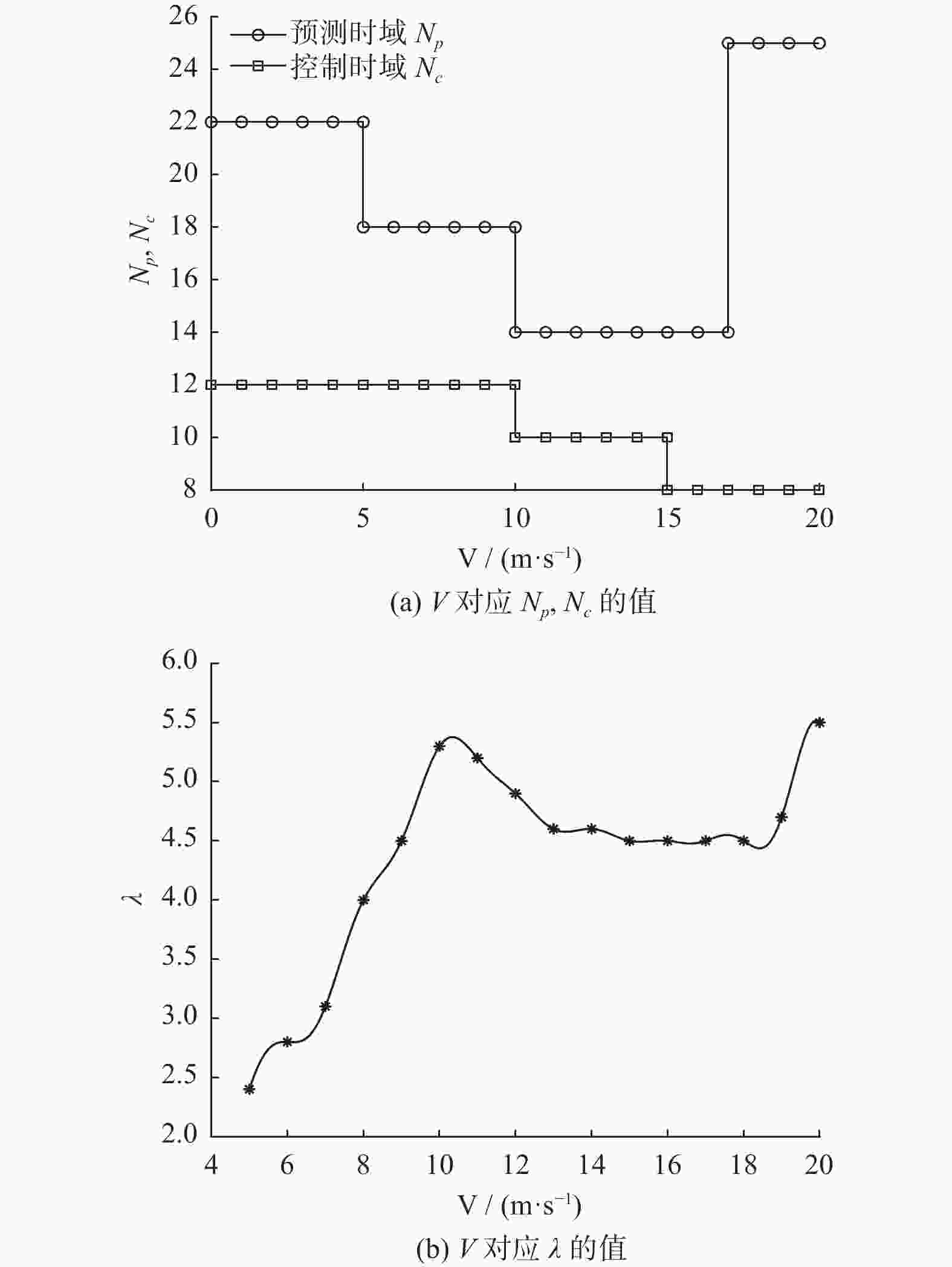
控制器参数 ${N_{\rm{p}}}$ ${N_{\rm{c}}}$ $\lambda $ MPC 20 20 5 PSO-MPC 25 8 5.5
下载: 导出CSV
-
[1] NI J J, CHEN Y N, CHEN Y, et al. A survey on theories and applications for self-driving cars based on deep learning methods[J] . Applied Sciences,2020,10(8):2749. doi: 10.3390/app10082749 [2] CLEMENTS L M, KOCKELMAN K M. Economic effects of automated vehicles[J] . Transportation Research Record,2017,2606(1):106 − 114. doi: 10.3141/2606-14 [3] 陈特, 陈龙, 徐兴, 等. 基于 Hamilton 理论的无人车路径跟踪控制[J] . 北京理工大学学报,2019,39(7):676 − 682. [4] ZHANG Y H, WANG W D, WANG W, et al. An Adaptive Constrained Path Following Control Scheme for Autonomous Electric Vehicles[J] . IEEE Transactions on Vehicular Technology,2022,71(4):3569 − 3578. doi: 10.1109/TVT.2022.3146134 [5] SUSUKI R, KAWAI F, NAKAZAWA C, et al. Parameter optimization of model predictive control using PSO[C]//Proceedings of 2008 SICE Annual Conference. Tokyo: IEEE, 2008: 1981 − 1988. [6] MOUMOUH H, LANGLOIS N, HADDAD M. Off-line Robustness Improvement of a Predictive Controller Using a Novel Tuning Approach Based on Artificial Neural Network[C]//Proceedings of 2020 IEEE 16th International Conference on Control & Automation (ICCA). Sapporo, Hokkaido: IEEE, 2020: 797 − 802. [7] 王银, 张灏琦, 孙前来, 等. 基于自适应 MPC 算法的轨迹跟踪控制研究[J] . 计算机工程与应用,2021,57(14):251 − 258. doi: 10.3778/j.issn.1002-8331.2007-0015 [8] XU S B, PENG H. Design, analysis, and experiments of preview path tracking control for autonomous vehicles[J] . IEEE Transactions on Intelligent Transportation Systems,2019,21(1):48 − 58. [9] HUBER M F. Recursive Gaussian process: On-line regression and learning[J] . Pattern Recognition Letters,2014,45:85 − 91. doi: 10.1016/j.patrec.2014.03.004 [10] ARANY R R, AUWERAER H V D, SON T D. Learning Control for Autonomous Driving on Slippery Snowy Road Conditions[C]//Proceedings of 2020 IEEE Conference on Control Technology and Applications (CCTA). Montréal: IEEE, 2020: 312 − 317. [11] SEEGER M. Gaussian processes for machine learning[J] . International journal of neural systems,2004,14(2):69 − 106. doi: 10.1142/S0129065704001899 -
下载:
点击查看大图
计量
- 文章访问数: 190
- HTML全文浏览量: 58
- PDF下载量: 164
- 被引次数: 0
